Эта тема обращается к программному обеспечению Simscape™ Multibody™ First Generation. Библиотека первого поколения будет скоро удержана от использования. Чтобы избежать проблем совместимости, создайте любые новые модели и преобразуйте любые существующие модели с помощью блоков второго поколения — доступные путем ввода команды smlib в командной строке MATLAB®.
Прежде, чем работать посредством этого исследования, консультируйтесь с предварительной системой управления О Контроллерах и Объектах. Второе исследование системы управления, Разрабатывая и Улучшая Контроллеры, основывается на результатах и концепциях этого исследования.
В дополнение к Simulink® и продукту Simscape Multibody, это исследование использует продукт Control System Toolbox.
Это первое тематическое исследование системы управления реализует систему управления платформы Стюарта со стандартом, предварительно оптимизированным контроллер пропорциональной интегральной производной (PID). Это вводит вас полной модели и неконтролируемому движению платформы Стюарта. Это затем показывает, как ПИД-регулятор работает, как сделать его более реалистичным с отфильтрованной производной, и как использовать классические методы управления, чтобы анализировать ответ ПИДа.
Откройте mech_stewart_control модель.
Модель системы управления платформы Стюарта
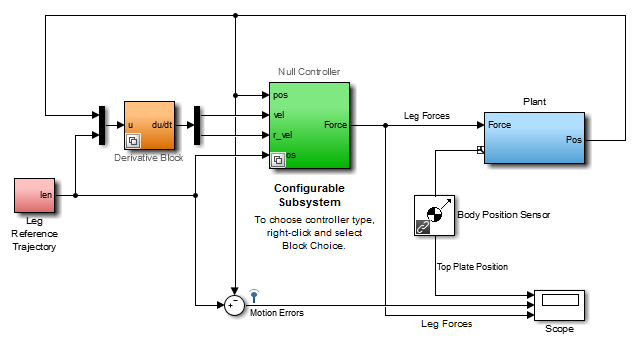
Зеленая подсистема контроллера соединяется с активированной подсистемой в связанной модели библиотеки, mech_stewart_controllers. Начальная настройка Пустому Контроллеру, который не налагает сил вообще на платформу, синяя подсистема маркировала Plant. Откройте Пустую Подсистему контроллера. Этот контроллер принимает информацию о траектории, но выходной нуль для наложенной силы.
Журналирование сигнала фиксирует ошибки движения. Вы используете эту функцию позже, чтобы анализировать производительность контроллера.
Видеть библиотеку подсистемы контроллера:
Щелкните правой кнопкой по блоку Null Controller и выберите Link Options, затем Go To Library Block. mech_stewart_controllers библиотека открывается подсвеченным блоком Template.
Можно установить эту активированную подсистему тремя способами, и вы используете все три в этом тематическом исследовании: Null Controller, PID Controller и H_inf Controller.
Откройте подсистему контроллера в каждой установке, чтобы исследовать ее блок-схему.
Дважды кликните блок Template, чтобы видеть проект подсистемы контроллера. Три возможных настройки подсистемы перечислены в диалоговом окне Шаблона.
Закройте модель библиотеки.
Вы выбираете настройку подсистемы, на самом деле используемую для симуляции назад в исходной модели, mech_stewart_control.
Щелкните правой кнопкой по блоку Null Controller и выберите Block Choice. Три возможных подсистемы от mech_stewart_controllers библиотеки перечислены с выбранным Null Controller.
Видеть динамические настройки для модели системы управления:
Откройте подсистему Объекта и оранжевый блок Machine Environment. В диалоговом окне блока найдите вкладку Parameters. Вектор силы тяжести указывает в отрицательном направлении z.
Затем найдите вкладку Constraints. Constraint solver type является Machine precision, и флажок Use robust singularity handling устанавливается. Для этой модели такая комбинация является самой устойчивой.
Закройте диалоговое окно и подсистему.
Из меню Simulation откройте Параметры конфигурации. Найдите узел Simscape Multibody 1G, область Diagnostics. В этой симуляции автоматически отмечены соединения сокращения.
Поскольку платформа Стюарта является машиной с обратной связью, симуляция сокращает одно соединение в каждом замкнутом цикле, сформированном этими двумя пластинами и парой участков во время симуляции и отмеченный красным X. Смотрите Степени свободы подсчета в Платформе Стюарта и Идентификации Simulink и Механических состояний Платформы Стюарта.
Закройте диалоговое окно.
Сначала моделируйте платформу Стюарта без любых сил управления. Платформа перемещается под влиянием силы тяжести и начальных условий только. Ссылочная траектория не важна, потому что она не используется, чтобы сгенерировать любые силы управления.
Смотреть естественное или неконтролируемое движение платформы Стюарта:
Откройте блок Scope. Окно Scope отображает три измерения:
Положение главного CG пластины
Управляйте ошибками
Управляйте силами, прикладывавшими, чтобы переместить участки
Запустите модель. Отследите падающую платформу путем наблюдения Главного графика Положения Пластины в окне Scope. Поскольку контроллер ничего не делает в этой версии модели, ошибки управления и силы не важны.
Теперь измените модель, чтобы управлять движением платформы Стюарта с линейной системой с обратной связью пропорциональной интегральной производной (PID).
Начальные настройки контроллера обсуждены в Моделировании Контроллеров и Инициализации Модели Платформы Стюарта. Здесь вы реализуете две версии этого контроллера, неподходящего и biproper. Смотрите Анализ Ответа ПИД-регулятора для больше.
Переключите подсистему контроллера модели путем щелчка правой кнопкой по (зеленому) блоку подсистемы управления, выбора Block Choice, затем PID Controller. Имя блока изменяется от Пустого Диспетчера на ПИД-регулятор. Откройте его.
Подсистема ПИД-регулятора платформы Стюарта
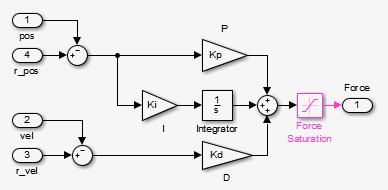
Это - ПИД линейная система управления с обратной связью, копия исходной подсистемы, содержавшейся в mech_stewart_controllers образцовой библиотеке. Передаточная функция управления имеет форму K i/s + K ds + K p. Управление получает K i, K p, и K d в их соответствующих блоках ссылается на переменные Ki, Kp, Kd, заданный в вашей рабочей области. Проверяйте их инициализированные значения:
Ki, Kp, Kd
Ki = 10000
Kp = 2000000
Kd = 45000Моделируйте платформу Стюарта с ПИД-регулятором.
Откройте Осциллограф и запустите симуляцию.
Наблюдайте управляемое движение платформы Стюарта. Осциллограф показывает, как платформа первоначально не следует за ссылочной траекторией, которая начинает в различном положении с домашней настройки платформы. Ошибки движения и силы на участках являются значительными. Заметьте также, что силы участка насыщают во время начального переходного процесса.
Платформа перемещается быстро, чтобы синхронизироваться со ссылочной траекторией, и силы участка и ошибки движения становятся намного меньшими.
Движение платформы Стюарта и силы с ПИД-регулятором
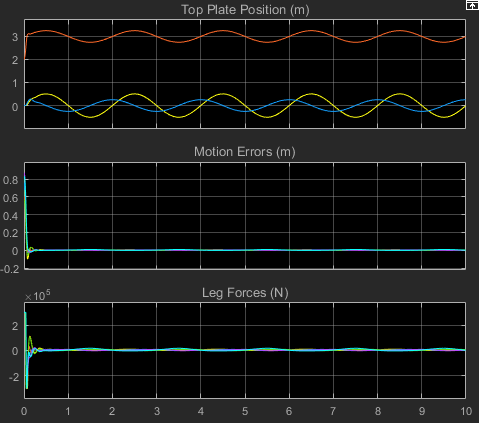
Закон о надзоре ПИДа требует производной времени и фактического и ссылочного движения. Для большего реализма объект платформы Стюарта использует блок Body Sensor, чтобы обнаружить только фактическое положение платформы, оставляя скорость, которая будет вычислена контроллером. Нахождение ссылочных и фактических скоростей требует берущих числовых производных ссылочных и фактических траекторий, которые каждый состоит из шести длин участка как функции времени.
Модель дает вам два способа сделать это. Можно переключить числовую производную конфигурируемую подсистему, чтобы реализовать также. Этот блок соединяется с библиотекой mech_stewart_control_deriv, который содержит две реализации подсистемы. Щелкните правой кнопкой по числовому производному (оранжевому) блоку и выберите Block Choice, затем Derivative Block или Filtered Derivative.
Наиболее предпочтительное (неподходящее) использование блок Derivative Simulink. Этот блок дает точные но идеализированные результаты. Этим выбором является значение по умолчанию.
Второй выбор (biproper) применяет фильтр Передачи блоки Fcn в области Лапласа прежде, чем преобразовать сигналы назад к временному интервалу. Этот выбор ближе к реалистической реализации.
Передаточная функция имеет каноническую форму As/(s+A). Передаточная функция действует как низкочастотный полосовой фильтр к ослаблению детали производной на масштабах времени короче, чем 2π/A. Передача блоки Fcn использует переменную A рабочей области, представляющую A. Его значение должно быть установлено приблизительно к 50 - 100 раз переменной freq частоты движения. Сохраните Передачу числителями Fcn и знаменателями в их канонической форме с точки зрения A. Инициализированным значением является A = 100*π.
Отфильтрованная производная передаточной функции более реалистична, за счет некоторой погрешности из-за переходных процессов. Отличайтесь отфильтрованное производное поведение путем корректировки A в рабочей области. Нежелательное переходное поведение хуже для меньшего A.
Домашняя настройка платформы Стюарта является симметричным равновесием главной пластины. Позже в этом исследовании, необходимо моделировать платформу в покое. Если при запуске модель в этом состоянии, силы управления являются нулем, и главная пластина не перемещается.
Сохраните Фильтрованную Производную опцию и моделируйте эту статическую траекторию.
Откройте подсистему Траектории Ссылки Участка. Найдите Переключатель Траектории направо. Дважды кликните Переключатель к вниз положение.
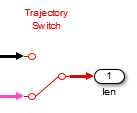
Ссылочная траектория теперь задает статическую ссылочную траекторию: платформа, остающаяся все еще со всеми участками в той же постоянной длине.
Закройте подсистему и запустите симуляцию. Наблюдайте статическую платформу или в Осциллографе, окне визуализации или в обоих.
После повторного выполнения модели, сброс Переключатель Траектории назад к.
Этот раздел требует Control System Toolbox.
Можно узнать больше об эффекте ПИД-регулятора на движении платформы Стюарта с двумя методами теории управления, s - плоскость и частотная характеристика, оба на основе Преобразования Лапласа. Для получения дополнительной информации смотрите Ссылки и документацию для Control System Toolbox™.
Закон о надзоре ПИДа является введенным выводом отношением, передаточная функция которого
где усиления K являются действительными и неотрицательными. Третья версия является формой нулей и полюсов.
C(s) является неподходящим, повышающийся без предела для большого s и имеющий больше нулей (два), чем полюса (один, в s = 0). Полюса определяют ответ контроллера в течение более длительных времен. Нули изменяют, как быстро контроллер приближается к устойчивому состоянию, особенно если нуль приближается и почти отменяет полюс. Получите установившееся, умножив передаточную функцию на s, затем позволив s исчезнуть.
В законе о надзоре ПИДа K, который i получаю, является установившимся ответом. Переходное поведение наиболее строго под влиянием самой высокой степени s (K d термин), затем следующей степенью s (K p термин), и так далее. Когда вы отличаетесь усиления, появляются различные поведения.
Если K i исчезает, ответ является всем переходным процессом с пустым устойчивым состоянием. Один нуль совпадает с и отменяет полюс. Другой нуль является-Kp/Kd.
Если K d исчезает, только один нуль остается в s =-Ki/Kp.
Если 4KdKi> K p2, нули становятся комплексными и отъезжают действительный s - ось.
Если усиление находится больше в более высоких степенях s, переходный ответ более силен.
Если усиление находится больше в более низких степенях s, переходный ответ подавлен, и установившийся ответ появляется более быстро.
Простой закон о надзоре ПИДа, с обычной производной, дает начало неподходящей передаточной функции C(s). Изменение обычной производной к отфильтрованной производной смягчает поведение измененного контроллера c(s) в большом s.
Эта функция является biproper, имея два нуля и два полюса, соответственно, в
Восстановите неподходящий закон о надзоре C(s) путем разрешения A → ∞.
Поскольку C(s) является неподходящим, Control System Toolbox не может полностью анализировать простой ответ ПИД-регулятора. Однако отфильтрованный производный альтернативный c(s) приводит к результатам, подобным обычной производной. Полный анализ c(s) возможен.
С командой tf задайте линейный, независимый от времени (LTI) объекты передаточной функции для C(s) и c(s), затем анализируйте их с Linear System Analyzer.
numC = [Kd Kp Ki]; % Improper numerator denomC = [1 0]; % Improper denominator cImproper = tf(numC,denomC) % Improper transfer function numc = [Kd*A+Kp Kp*A+Ki Ki*A]; % Biproper numerator denomc = [1 A 0]; % Biproper denominator cBiproper = tf(numc,denomc) % Biproper transfer function
Можно также преобразовать C(s) и c(s) к пространству состояний и нулям и полюсам (ZPK) формы. Последний особенно полезен. Введите help zpk для получения дополнительной информации.
zpk(cImproper) % Convert cImproper to zero-pole-gain zpk(cBiproper) % Convert cBiproper to zero-pole-gain
Полезная функция zpkdata извлекает нули, полюса и усиление от диспетчера ZPK-формы.
Теперь откройте интерфейс Linear System Analyzer путем ввода linearSystemAnalyzer.
Выберите меню File, затем Import. Диалоговое окно Import System Data открывается.
В Import from area выберите опцию Workspace и, под Systems in Workspace, обеими записями, cImproper и cBiproper. Нажмите OK.
Щелкните правой кнопкой в окне графика Linear System Analyzer, чтобы просмотреть аналитические опции под Plot Types и Characteristics.
С c(s) можно использовать все функции Linear System Analyzer. Ограничиваются ваши допустимые опции для анализа C(s).
Предвещание и Предвещает графики Значения, показывают частотной характеристике C(s) для мнимого s = j ω.
График Полюса/Нуля показывает местоположение полюсов и нули C(s).
Отобразите и C и системы c одновременно и сравните графики Предвещания и Полюса/Нуля.
Диаграммы Боде подобны для маленького s (долгое время). Для большого s (короткое время), повышения C(s) без предела, в то время как c(s) выравнивается и приводит к лучшему поведению контроллера.
Графики Полюса/Нуля показывают, что C(s) имеет один полюс и c(s) два полюса, общий, являющийся 0. Обе передаточных функции имеют два нуля. Можно определить местоположение всех их с функциями zero и pole. Обратите внимание на то, что один нуль почти идентичен между C(s) и c(s), в то время как другой переключен существенно. Это пересменки и смягчает переходное поведение c(s) по сравнению с C(s) для большего s (короткое время).
Исследуйте графики Шага и Импульса на c(s) также. Эти графики показывают поведение времени контроллера c(s) для ступенчатых и импульсивных входных параметров.