Эта тема обращается к программному обеспечению Simscape™ Multibody™ First Generation. Библиотека первого поколения будет скоро удержана от использования. Чтобы избежать проблем совместимости, создайте любые новые модели и преобразуйте любые существующие модели с помощью блоков второго поколения — доступные путем ввода команды smlib в командной строке MATLAB®.
Этот раздел объясняет существенные детали моделирования платформы Стюарта в среде Simscape Multibody. Чтобы понять раздел лучше, используйте любую модель верхнего уровня от тематических исследований, кроме моделей Обрезки и Линеаризации Через Обратную Динамику. Они отличаются, потому что они испытывают недостаток в подсистеме контроллера и состоят из одной только модели объекта управления.
Модель системы управления, mech_stewart_control, является примером этого раздела.
В трех из тематических исследований большая модель системы управления содержит подсистему Объекта, которая включает платформу.
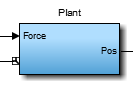
Подсистема Объекта моделирует подвижные части платформы Стюарта, участки и главную пластину. Откройте эту подсистему.
Модель платформы Стюарта (версия системы управления)
Каждый из участков является экземпляром блока библиотеки, расположенного в другой модели библиотеки, mech_stewartplatform_leg или mech_stewart_control_equil_leg.
Выберите одну из подсистем участка и щелкните правой кнопкой. Выберите Link Options, затем Go To Library Block, чтобы открыть эту библиотеку.
Откройте блок библиотеки маскированный, Подсистему Участка, и отдельное Тело и Объединенные блоки, которые составляют целый участок.
Теперь закройте блоки, подсистемы и соединенные библиотеки и возвратитесь к модели верхнего уровня.
Кроме Обрезки и Линеаризации Посредством Обратного исследования Динамики, модели платформы Стюарта содержат контроллеры, налагающие приводящие в действие силы, которые ведут движение платформы следовать максимально тесно за номинальной или ссылочной траекторией. Реализация контроллера требует вычисления ошибок движения, различия ссылочных и фактических движений платформы. Все модели тематического исследования используют управление пропорциональной интегральной производной (PID).
Каждый образцовый контроллер требует ссылочной траектории.
Откройте подсистему Траектории Ссылки Участка.
Этот набор блоков генерирует набор шести длин участка, как функции времени, соответствуя желаемой траектории для главной пластины.
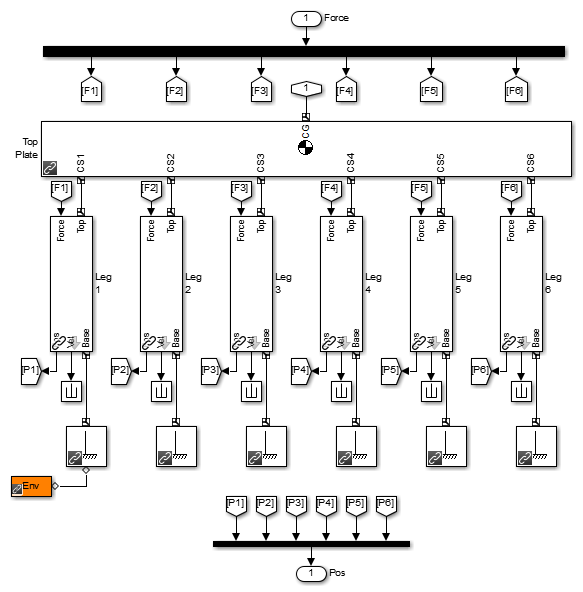
Откройте подсистему под названием Главная Ссылка Пластины. Этот набор блоков генерирует ссылочную траекторию с точки зрения линейного положения и трех углов ориентации как функция времени. Переменная freq рабочей области устанавливает частоту ссылочного движения.
Подсистема траектории ссылки платформы Стюарта (версия системы управления)
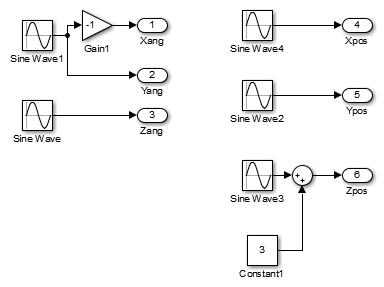
Ссылочная траектория обеспечила синусоидальные функции использования времени, чтобы задать вращательные и переводные степени свободы.
Если вы хотите, вы можете разработка и реализация другая ссылочная траектория вашего выбора и заменять эту подподсистему.
Независимо от того, что выходит из Главной Ссылки Пластины, Траектория Ссылки Участка подсистемы принимает переводную position/three-angle форму для главной пластины. Остальная часть подсистемы Траектории Ссылки Участка преобразовывает эти шесть степеней свободы (DoFs) в эквивалентный набор шести DoFs, выраженных как длины шести участков платформы. Ссылочная траектория вывод подсистемы является с шестью векторами из этих длин участка.
Сила приведения в действие на участке r является функцией ошибки движения. Ошибка требует нахождения мгновенной длины каждого участка от положений верхних и нижних точек контакта того участка.
Определение длины участка платформы Стюарта
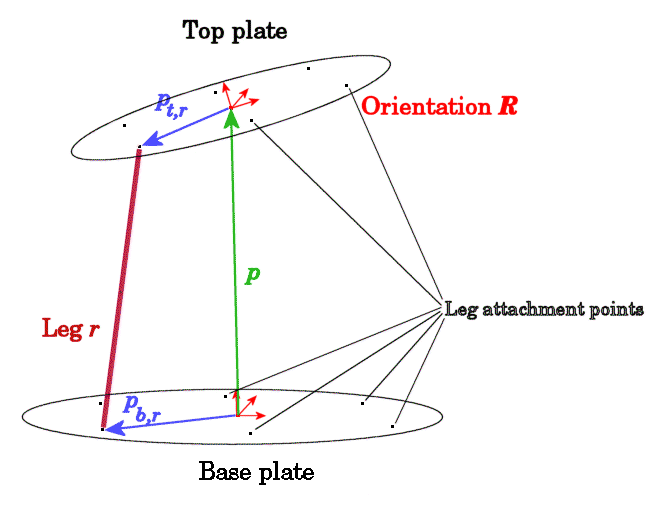
Ошибка движения является различием желаемой или ссылочной длины участка и его мгновенной или фактической длины:
Ссылочная длина L traj (t) дана как функция времени выводом подсистемы Траектории Ссылки Участка. Векторы p, p t, r, и p b, r задан в предыдущей фигуре. Ортогональная матрица вращения R задает ориентацию главной пластины относительно нижней части.
Все модели платформы Стюарта используют простой ПИД-регулятор и Объединенные блоки Датчика, чтобы измерить движение. Самая простая реализация управления траекторией должна прикладывать силы к объекту, пропорциональному ошибке движения. Обратная связь ПИДа является стандартной формой линейного управления.
Закон о надзоре ПИДа является линейной комбинацией переменной, обнаруженной датчиком, его интегралом времени и его первой производной. Этот ПИД-регулятор платформы Стюарта использует ошибки положения участка E r и их интегралы и скорости. Закон о надзоре для каждого участка r имеет форму:
Контроллер прикладывает силу приведения в действие действие F, r вдоль участка.
Если E r положителен, участок слишком короток, и действие F, r положителен (расширяемый).
Если E r отрицателен, участок является слишком длинным, и действие F, r отрицателен (сжимающий).
Если E r является нулем, участок имеет точно желаемую длину, и действие F, r является нулем.
Действительный, неотрицательный K p, K i, и K d является, соответственно, пропорциональным, интегралом и производными усилениями, которые модулируют сигналы датчика обратной связи в законе о надзоре:
Первый срок пропорционален мгновенной ошибке положения участка или отклонению от ссылки.
Второй срок пропорционален интегралу ошибки положения участка.
Третий срок пропорционален производной ошибки положения участка.
Результатом является действие F, r, сила привода (вход), примененный контроллером к участкам. Пропорциональное, интеграл и производные условия имеют тенденцию делать главные точки крепления участков p t, r, чтобы следовать за ссылочными траекториями путем подавления ошибки движения.
Тематическое исследование, О Контроллерах и Объектах, обсуждает движение платформы управления более подробно. В том исследовании вы также используете контроллер H-бесконечности, а также используете передаточные функции, чтобы взять производные движения.
Кроме того, консультируйтесь со Ссылками.
Когда представление физических компонентов модели платформы Стюарта с Simscape Multibody блокируется и компоненты элемента управления с блоками Simulink®, необходимо задать геометрию его начального состояния и массовые параметры тел платформы Стюарта. Несмотря на то, что каждое тематическое исследование использует различную модель, все инициализируют конфигурацию платформы и настройку контроллера в распространенном способе.
Геометрический, масса, динамическая, и информация контроллера задана в диалоговых окнах блока путем ссылки на переменные в рабочем пространстве MATLAB. Скрипт сопровождает модели платформы Стюарта и устанавливает эти значения.
Выполнение этого скрипта конфигурирует блоки в их стартовом геометрическом состоянии с правильными массовыми свойствами для тел. Когда вы открываете его, каждая модель использует тот же скрипт инициализации в качестве функции предварительной нагрузки. Видеть эту установку,
Войдите в меню File и выберите Model Properties.
Затем в диалоговом окне, выберите вкладку Callbacks и найдите поле Model pre-load function.
Файлы инициализации платформы Стюарта
| Файл | Цель |
|---|---|
mech_stewart_studies_setup | Скрипт, чтобы заполнить рабочую область с геометрическим, динамическим, и данные контроллера. |
inertiaCylinder | Функция вызвана mech_stewart_studies_setup. Вычисляет основную инерцию твердого цилиндра. |
Скрипт сначала задает основные угловые модульные преобразования и оси. Система Мировой координаты (CS) расположена в центре неподвижной опорной плиты. Точки контакта на основной и главной пластине заданы относительно Мира. Эти определения включают угол смещения 60 градусов между основными и главными пластинами, радиусами и основных и главных пластин, высоты исходного положения главной пластины и векторов, указывающих вдоль участков. Массив главных точек переставлен так, чтобы тот же индекс представлял верхние и нижние точки контакта для того же участка.
Скрипт вычисляет закрученные назад и цилиндрические оси, используемые в объединенных блоках подсистем участка. Существует две закрученных назад оси для каждого Универсального соединения, которое соединяет бедро с главной пластиной, одним цилиндрическим и одной закрученной назад осью для линейного движения Цилиндрического соединения, соединяющего бедра и голени и две закрученных назад оси для каждого блока Universal, который соединяет голень с опорной плитой. Скрипт затем конфигурирует все 13 двигающих тел путем определения систем координат в центре тяжести (CG) каждого.
Домашняя настройка главной пластины является симметричным равновесием: плоский, с равными длинами участка, заданными вектором рабочей области leg_length.
Скрипт задает массовые свойства всех тел. Они включают тензоры инерции и массы для главной пластины, подопочного щитка и участков. Массовое вычисление свойств принимает, что платформа сделана со сталью. Скрипт вызывает функциональный inertiaCylinder, чтобы вычислить тензоры инерции и массы участков и главных и опорных плит, учитывая существенную плотность, длину и внутренние и внешние радиусы цилиндров участка, и толщины и радиусы главных и опорных плит.
В его последних шагах скрипт задает движение и константы управления как переменные рабочей области: частота движения, производное сокращение фильтрации, насыщение силы привода участка и усиления контроллера. Каждая модель тематического исследования использует некоторых или все эти константы, которые можно изменить, как желаемый.
Действительные приводы силы, насыщают на определенном уровне силы. Блок Force Saturation ограничивает силу приведения в действие значением переменной force_act_max рабочей области.
Интеграл (I) часть ПИД-регулятора показывает расширенное время отклика, полным эффектом которого управляет отношение K i к K p. Интегратор для меня отделяется, имеет ненулевое поле Initial condition, заданное переменной initCondI рабочей области, корректируемой, чтобы компенсировать начальное переходное поведение. Скрипт инициализирует свое значение к
(upper_leg_mass+lower_leg_mass+(top_mass*1.3/6))*9.81/Ki
соответствие участку обеспечивает в симметричном равновесии.
Движение и константы фильтрации
| Динамическая функция | Переменная рабочей области | Связанная собственная частота | Связанный масштаб времени |
|---|---|---|---|
| Главное движение пластины | freq = π rad/s | freq/2π = 0,5 Гц | 2π/freq = 2 с |
| Фильтрованное производное сокращение | A = 100*freq = 100π рад/с | A/2π = 50 Гц | 2π/A = 0,02 с |
Константы ПИД-регулятора
| Динамическая константа | Переменная рабочей области |
|---|---|
| Обеспечьте насыщение | force_act_max = 3e5 ньютоны (Н) |
| Интеграл (I) усиление | Ki = 1e4 (ньютоны/метр/вторые) (N/m-s) |
| Пропорциональный (P) усиление | Kp = 2e6 ньютоны/метр (N/m) |
| Производная (D) усиление | Kd = 4.5e4 newtons-seconds/meter (N-s/m) |
В целях анализа движения Simscape Multibody необходимо знать Simulink модели и механические состояния. Они отличны от степеней свободы системы (DoFs) и зависят от аналитического режима, который вы выбираете.
Если вы используете контроллер или другую подсистему, составленную из чистых блоков Simulink с вашей платформой Стюарта, ваша сила модели содержат состояния Simulink. Например, Интегратор и Передача, Fcn блокирует каждого, имеют ассоциированную страну, и блоки Пространства состояний могут иметь многих.
Контроллер платформы Стюарта значения по умолчанию является подсистемой ПИДа, которая интегрирует шесть сигналов обратной связи и таким образом имеет шесть состояний Simulink. В Контроллерах Анализа и Разработке и Улучшении исследований Контроллеров, можно также принять решение использовать отфильтрованную производную, которая имеет 12 передаточных функций и таким образом добавляет 12 состояний Simulink.
Механическая система, смоделированная с Объединенными блоками, содержит механические состояния, отличные от состояний Simulink, которые включают и объединенное положение и скорость. В режиме Forward Dynamics платформа Стюарта содержит 52 древовидных состояния, от которых 12 независимы.
Соединения и их связанный DoFs обсуждены в подсчете Степеней свободы в Платформе Стюарта.
Объединенные Примитивы и состояния. Каждое Соединение состоит из одного или нескольких примитивов. Положение и скорость объединенного примитива у каждого есть состояние. Платформа Стюарта имеет 36 объединенных примитивов и таким образом потенциально 72 состояния.
Сокращение Соединений и Получение Древовидных состояний. Поскольку платформа Стюарта закрыла топологию, модель Simscape Multibody сократит пять из Соединений, чтобы прибыть в эквивалентную открытую топологию или древовидную машину. Эти Соединения заменяются внутренне эквивалентными сокращающими ограничениями.
Пять Universals и 5*2*2 = 20 объединенных примитивов устраняются этот путь. Эквивалентная открытая машина таким образом имеет 72 - 20 = 52 древовидных состояния.
Подсчет Сокращающих Ограничений. Не все эти состояния независимы. Существует 40 эквивалентных ограничений, которые заменяют Соединения сокращения.
Каждое сокращение Universal налагает одно вращательное и три ограничения положения.
Каждое ограничение также ограничивает соответствующую скорость.
Существует пять Соединений сокращения.
Таким образом существуют 5*2*4 = 40 невидимых ограничений, сгенерированных сокращением.
Нахождение независимых государств. Таким образом модель платформы Стюарта имеет 52 - 40 = 12 независимых механических состояний, соответствуя шести независимым DoFs и их скоростям.
Можно также анализировать движение платформы Стюарта в обратной динамике и определить местоположение установившихся рабочих точек.
Поскольку платформа Стюарта является машиной с обратной связью, необходимо моделировать ее обратную динамику в режиме Kinematics.
Можно найти рабочие точки в режиме Trimming с командой trim Simulink.
И в обратной динамике и в случаях обрезки, состояниями Simulink, сопоставленными с примитивами соединения Simscape Multibody, не является DoFs, но (невидимые) сокращающие соединение ограничения, которые уменьшают древовидные состояния до независимых государств. Значения состояния измеряются, как хорошо ограничения удовлетворены. Нулевое значение означает, что ограничение удовлетворено отлично.
В механической детали модели платформы Стюарта существует 52 древовидных состояния и 12 независимых государств. Таким образом количества 52 - 12 модели Simscape Multibody = 40 сокращающих ограничений. В режимах Kinematics и Trimming эти 40 ограничений являются механическими состояниями.
Открытая Топология и Обратный Режим Динамики. Если бы платформа Стюарта имела открытую топологию, вы моделировали бы ее обратную динамику в режиме Inverse Dynamics вместо этого. Однако не было бы никаких замкнутых циклов, и симуляция не сократит Соединений. Без сокращения ограничений открытая машина топологии не имеет никаких состояний в режиме Inverse Dynamics или Trimming.
Для получения дополнительной информации о состояниях и циклах, рассмотрите следующие разделы:
Можно также рассмотреть справочную документацию команды для mech_stateVectorMgr.
Для получения дополнительной информации об аналитических режимах, смотрите Симуляцию и Анализ Механического Движения.
С открытым окном визуализации Simscape Multibody можно просмотреть движение платформы с разных точек зрения. Просмотрите платформу в xy - плоскость, сверху. Затем переключите представление на xz - или yz - плоскость.
Начальное состояние движения, заданного ссылочной траекторией, немного отличается от домашней настройки и генерирует начальный переходный процесс.