Эта тема обращается к программному обеспечению Simscape™ Multibody™ First Generation. Библиотека первого поколения удерживается от использования. Чтобы избежать проблем совместимости, создайте любые новые модели и преобразуйте любые существующие модели с помощью блоков второго поколения — доступные путем ввода команды smlib в командной строке MATLAB®.
Это тематическое исследование находит устойчивое состояние платформы Стюарта с режимом Simscape Multibody Kinematics. Вы задаете движения и определяете силы и крутящие моменты, чтобы произвести те движения (обратная проблема динамики). Если вы не знакомы с реализацией обратной динамики в среде Simscape Multibody, работаете через Силы Открытия от Движений прежде, чем делать попытку этого тематического исследования.
Используйте режимы Inverse Dynamics и Kinematics для обратного динамического анализа открытых - и системы закрытой топологии, соответственно. Платформа Стюарта имеет закрытую топологию и таким образом требует режима Kinematics. Если у вас есть рабочая точка, можно линеаризовать движение.
Чтобы завершить это тематическое исследование, необходимо использовать дополнительный продукт, Control System Toolbox .
Обрезка системы означает определять местоположение настройки своих состояний с определенными предшествующими условиями, наложенными на состояния и возможно их производные. В механическом контексте это означает внушительные условия на определенных положениях и скоростях, затем определяя остающиеся положения и скорости, таким образом, что целое состояние машины сопоставимо. Побочный продукт механической обрезки является определением сил/крутящих моментов, необходимых, чтобы произвести заданное движение. Эти состояния движения составляют или рабочую точку для обрезки. Обрезка проблем может иметь одно решение, больше чем один или ни один.
Чистая обратная динамика налагает предшествующие движения на все степени свободы. Затем все состояния определяются. (Непротиворечивость движений не гарантируется, но должна проверяться.) Только силы/крутящие моменты остаются, чтобы быть найденными.
Найти рабочую точку или устойчивое состояние для модели Simscape Multibody,
Используйте команду trim в Simulink®. См. Обрезающие Механические Модели.
Используйте более мощные методы, обеспеченные Control System Toolbox™ и Simulink Control Design™. Займитесь Контроллерами и Объектами.
Используйте режимы динамики инверсии Simscape Multibody. Можно управлять механическими состояниями модели непосредственно с приведением в действие движения, а не управлять ими через Simulink.
Вот файлы, необходимые для этого тематического исследования. Модели также вызывают скрипт инициализации и функцию. Откройте первую модель.
| Файл | Цель |
|---|---|
mech_stewart_control_equil | Модель Kinematics для определения платформы Стюарта обеспечивает равновесие |
mech_stewart_control_equil_leg | Модель Library участка платформы Стюарта для кинематического анализа |
mech_stewart_control_plant | Передайте модель динамики для линеаризации платформы Стюарта |
mech_stewartplatform_leg | Модель Library участка платформы Стюарта для прямого динамического анализа |
mech_stewart_control_equil модель имеет некоторую предварительную установку настройки не по умолчанию.
Параметры конфигурации
| Установка | Значение |
|---|---|
| Solver> Simulation time> Stop time | Секунды 0.005 |
| Data Import/Export | Time и States, выбранный> tout и xout |
| Simscape Multibody 1G> Diagnostics | Mark automatically cut joints выбран |
| Simscape Multibody 1G> Visualization | Display machines after updating diagram и Show animation during simulation выбран |
Среда машины
| Установка | Значение |
|---|---|
| Parameters> Analysis mode | Kinematics |
| Parameters> Machine Dimensionality | 3D Only |
| Constraints> Constraint solver type | Machine Precision |
| Constraints> Use robust singularity handling | Выбранный |
Шесть участков платформы Стюарта являются экземплярами основного участка, сохраненного в библиотеке mech_stewart_control_equil_leg. Это берет в качестве входных параметров сигналы приведения в действие движения, которые задают положение и скорость как функция времени. Сигналы положения задают движение платформы относительно начальной геометрической настройки.
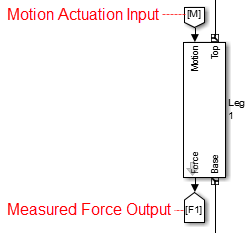
В mech_stewart_control_equil подсистема Движения задает движение как тривиальное: обнуляет для всех шести положений участка и скоростей. Таким образом, модель содержит платформу все еще в ее начальном состоянии.
Каждые выходные параметры участка платформы Стюарта вычисленная сила участка должны были поддержать движение, заданное приведением в действие движения. Эти шесть измеренных сил направлены к вашему рабочему пространству MATLAB блоком To Workspace.
Откройтесь К диалоговому окну Рабочей области.
Выходные силы хранятся в векторной переменной Forces. Блок сохраняет вектор силы только от последнего временного шага.
Закройтесь К диалоговому окну Рабочей области.
Теперь запустите mech_stewart_control_equil.
Нажмите Start и ожидайте симуляции, чтобы закончиться.
В вашей рабочей области найдите tout и xout. Это временные шаги и соответствующие значения состояния, соответственно.
В режиме Inverse Dynamics существует 40 механических состояний, считаемых Simulink, сопоставленным с механическими ограничениями. Консультируйтесь с Идентификацией Simulink и Механических состояний Платформы Стюарта.
Найдите Forces в рабочей области. Это шесть значений силы вдоль каждого участка, чтобы содержать платформу все еще против падения силой тяжести. Значения положительны (расширяемый) вдоль участков.
Знание установившихся сил должно было сохранить платформу все еще, вы теперь линеаризуете другую версию модели, mech_stewart_control_plant. Это имеет настройки, подобные mech_stewart_control_equil, за исключением того, что:
Analysis mode установлен в Forward Dynamics.
Время симуляции составляет 10 секунд.
Time и Output, tout и yout, соответственно, сохранены в рабочую область.
Откройте модель mech_stewart_control_plant.
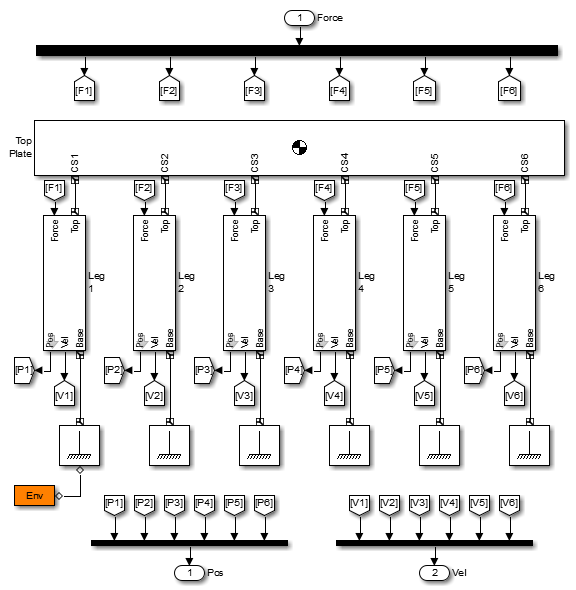
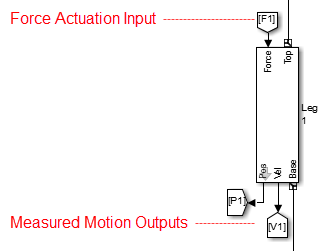
Эти шесть участков являются экземплярами mech_stewartplatform_leg библиотеки. Этот участок берет силу в качестве входа и выходного положения и скорости, в качестве подходящей для прямой динамики.
Стандартной образцовой входной переменной является u. Сигнал вектора силы является образцовым входом.
Сигналами радиус-вектора и вектора скорости являются образцовые выходные параметры. Выходная переменная Data Import/Export является yout и появится в вашей рабочей области, присвоенной с данными после того, как вы моделируете.
Закройте модель.
Можно моделировать mech_stewart_control_plant модель, не открывая его.
В командной строке войти
nomForces = Forces'; % Transpose the force vector
Линеаризуйте модель путем ввода
[A,B,C,D] = ...
linmod('mech_stewart_control_plant',[],nomForces);Аргументы, по порядку,
Имя модели
Образцовый вектор состояния (не используемый)
Образцовый входной вектор u = nomForces
Эти (неуменьшаемые) выходные матрицы являются стандартным представлением пространства состояний линеаризовавшей модели. Пробел задан x, u, и y, состоянием, входом и выходными векторами, соответственно.
Существует 52 состояния, 6 входных параметров и 12 выходных параметров. Таким образом A, B, C, D имеет размерности 52 52, 52 6, 12 52, и 12 6, соответственно. Не все эти матричные записи независимы.
Этот шаг требует Control System Toolbox.
Из 52 механических состояний платформа Стюарта имеет только 12 независимых государств, соответствуя шести степеням свободы (DoFs). Каждая степень свободы соответствует одному положению и одной скорости.
Чтобы устранить избыточные состояния, войти
[a,b,c,d] = ... minreal(A,B,C,D); 40 states removed.
в командной строке. a, b, c, матрицы d уменьшаются в размере до 12 12, 12 6, 12 12, 12 6, соответственно.
Смотрите Линеаризацию Открытой Топологии: Двойной Маятник и документация Simulink.
Обрезка в Режиме Кинематики и Линеаризация Платформы Стюарта в Рабочей точке представляют самый простой сценарий обрезки:
Все шесть степеней свободы (DoFs) определяются предшествующей спецификацией положений и скоростей. Это входные параметры к проблеме. Выходные параметры являются силами, необходимыми, чтобы поддержать заданное движение. Симуляция решает чистую обратную проблему динамики.
Фактические сигналы приведения в действие движения требуют, чтобы платформа содержала все еще относительно ее начальной геометрической настройки.
В более типичной проблеме обрезки вы задаете некоторые DoFs приведением в действие движения и оставляете другие свободными ответить силам/крутящим моментам. Такой сценарий является смешанной проблемой динамики. В среде Simscape Multibody можно решить такие проблемы в
Передайте режим Dynamics, где дерево утверждает (DoFs, соответствующий неразрезанным Соединениям), механические состояния
Режим Kinematics (закрытая топология), где сокращающие ограничения, которые заменяют Соединения сокращения, составляют механические состояния
Обратная Динамика (открывают топологию), где нет никаких механических состояний
Взаимозависимость инверсии и прямой динамики
| Приведите в действие степень свободы с... | Распознайтесь на степени свободы... |
|---|---|
| Силы/крутящие моменты | Движения |
| Движения | Силы/крутящие моменты |
Если вы хотите решить такую проблему для платформы Стюарта, вы должны
Используйте участок библиотеки с
Вход Force
Motion вывод
для каждого участка, моделируемого в прямой динамике. Вы приводите в действие его с силой и измеряете ее движение. Используйте mech_stewartplatform_leg библиотеку блоков.
Используйте участок библиотеки с
Вход Motion
Force вывод
для каждого участка, моделируемого в обратной динамике. Вы приводите в действие его с движением и измеряете соответствующую силу. Используйте mech_stewart_control_equil_leg библиотеку блоков.
Установившиеся выходные параметры являются в свою очередь входными параметрами для линеаризации.
Взаимозависимость обрезки и линеаризации
| Обрезка Вывода становится... | ... Вход линеаризации |
|---|---|
| Измеренные движения становятся... | ... Сигналы приведения в действие движения |
| Измеренные силы/крутящие моменты становятся... | ... Обеспечьте/закрутите сигналы приведения в действие |
Выполнить линеаризацию вашей системы,
Создайте различную модель в режиме Forward Dynamics, который берет
Установившиеся силы как входное приведение в действие силы линеаризации
Установившиеся движения как линеаризация вводят приведение в действие движения
Линеаризуйте с linmod.
linmod('forward_dynamics_model_to_linearize', state, input)Эта команда может подать образцовые входные параметры в линеаризовавшую симуляцию как аргумент команды. Дополнительную информацию см. в ссылке команды.