Формирование цикла смешанной чувствительности

Популярным альтернативным подходом к формированию цикла loopsyn является H _∞ формирование цикла смешанной чувствительности, которое реализовано командой программного обеспечения Robust Control Toolbox™:

K=mixsyn(G,W1,[],W3)

С контроллером mixsyn синтез, ваша производительность и уравнения спецификаций робастности устойчивости (2-2) и (2-4) объединены в одну спецификацию нормы бесконечности формы

${‖ T_{y_{1} u_{1}} ‖}_{\infty} \leq 1$

где (см. MIXSYN H ∞ Ty1 u1 Формирования Цикла Смешанной Чувствительности):

$T_{y_{1} u_{1}} \overset{d e f}{=} [\begin{matrix} W_{1} & S \\ W_{3} & T \end{matrix}] .$

Термин ${‖ T_{y_{1} u_{1}} ‖}_{\infty}$ называется функцией стоимости смешанной чувствительности, потому что она штрафует и чувствительность S (s) и дополнительную чувствительность T (s). Формирование цикла достигается, когда вы выбираете W₁, чтобы иметь целевую форму цикла для частот ω <_ωc, и вы выбираете 1/W3, чтобы быть целью для ω> _ωc. В выборе спецификаций проекта W ₁ и W ₃ для проектирования контроллера mixsyn, необходимо гарантировать, что перекрестная частота на 0 дБ для Диаграммы Боде W ₁ ниже перекрестной частоты на 0 дБ 1/W3, как показано в Спецификациях Сингулярного значения на L, S, и T, так, чтобы был разрыв для желаемой формы цикла, Gd, чтобы передать между производительностью связал W ₁и связанная робастность $W_{3}^{- 1}$ . В противном случае ваша производительность и требования робастности не будут достижимы.

MIXSYN H _∞ _{Ty1 u1} Формирования Цикла Смешанной Чувствительности

Проектирование контроллера формирования цикла смешанной чувствительности

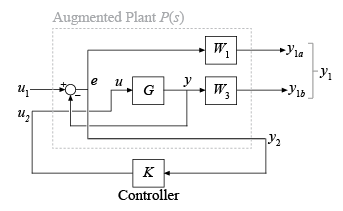
Чтобы сделать H mixsyn _∞ проект синтеза смешанной чувствительности на модели HiMAT, запустите с модели объекта управления G, обсужденный в Проектировании контроллера Формирования Цикла Смешанной Чувствительности. Следующий код воссоздает ту модель объекта управления.

ag =[ -2.2567e-02  -3.6617e+01 -1.8897e+01  -3.2090e+01   3.2509e+00  -7.6257e-01;
       9.2572e-05  -1.8997e+00   9.8312e-01  -7.2562e-04  -1.7080e-01 -4.9652e-03;
       1.2338e-02   1.1720e+01  -2.6316e+00   8.7582e-04  -3.1604e+01  2.2396e+01;
       0            0            1.0000e+00   0            0           0;
       0            0            0            0           -3.0000e+01  0;
       0            0            0            0            0  -3.0000e+01];
bg = [ 0     0;
       0     0;
       0     0;
       0     0;
       30     0;
       0    30];
cg = [ 0     1     0     0     0     0;
       0     0     0     1     0     0];
dg = [ 0     0;
       0     0];
G = ss(ag,bg,cg,dg);

Настройте производительность и границы робастности, W1 и W3.

s = zpk('s'); % Laplace variable s
MS = 2; AS = .03; WS = 5;
W1 = (s/MS+WS)/(s+AS*WS);
MT = 2; AT = .05; WT = 20;
W3 = (s+WT/MT)/(AT*s+WT);

Вычислите смешанную чувствительность H-бесконечности оптимальный контроллер K1 с помощью mixsyn.

[K1,CL1,GAM1] = mixsyn(G,W1,[],W3);

Затем вычислите ответы системы с обратной связью. Вычислите цикл L1, чувствительность S1 и дополнительная чувствительность T1.

L1 = G*K1;
I = eye(size(L1));
S1 = feedback(I,L1); % S=inv(I+L1);
T1 = I-S1;

Наконец, постройте ответы частотного диапазона и временной интервал.

step(T1,1.5);
title('\alpha and \theta command step responses');

figure;
sigma(I+L1,'--',T1,':',L1,'r--',W1/GAM1,'k--',GAM1/W3,'k-.',{.1,100})
legend('1/\sigma(S) performance','\sigma(T) robustness','\sigma(L) loopshape',...
       '\sigma(W1) performance bound','\sigma(1/W3) robustness bound')

Смотрите также

mixsyn

Документация