Exponenta Banner

ncfsyn

Цикл, формирующий проект с помощью метода Перчаточника-McFarlane

свернуть все на странице

ncfsyn реализует метод для разработки контроллеров, который использует комбинацию формирования цикла и устойчивой стабилизации, как предложено в [1]-[2]. Функция вычисляет Перчаточника-McFarlane, H ∞ нормировал взаимно-простой факторный формирующий цикл контроллер K для объекта G с весами предварительного компенсатора и посткомпенсатора W 1 и W 2. Функция принимает настройку позитивных откликов следующего рисунка.

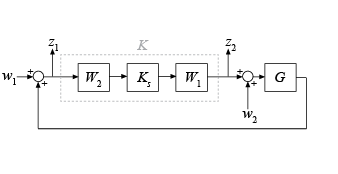
Чтобы задать отрицательную обратную связь, замените G –G. Контроллер Ks стабилизирует семейство систем, данное шаром неуверенности в нормированных взаимно-простых факторах имеющего форму объекта Gs = W 2GW1. Итоговый контроллер K, возвращенный ncfsyn, получен как K = W 1KsW2.

Синтаксис

[K,CL,gamma,info] = ncfsyn(G)
[K,CL,gamma,info] = ncfsyn(G,W1)
[K,CL,gamma,info] = ncfsyn(G,W1,W2)
[K,CL,gamma,info] = ncfsyn(G,W1,W2,'ref')

Описание

[K,CL,gamma,info] = ncfsyn(G) вычисляет Перчаточника-McFarlane, H ∞ нормировал взаимно-простой факторный формирующий цикл контроллер K для объекта G с W 1 = W 2 = I. CL является системой с обратной связью от воздействий w 1 и w 2 к выходным параметрам z 1 и z 2. Функция также возвращает H ∞ оптимальная стоимость gamma и структура, содержащая дополнительную информацию о результате.

пример

[K,CL,gamma,info] = ncfsyn(G,W1) вычисляет контроллер, использующий вес перед компенсатором, который вы задаете в W1 и W 2 = I.

[K,CL,gamma,info] = ncfsyn(G,W1,W2) вычисляет контроллер, использующий заданный вес перед компенсатором W1 и вес посткомпенсатора W2.

[K,CL,gamma,info] = ncfsyn(G,W1,W2,'ref') вычисляет контроллер со ссылочной командой, как в системе следующего рисунка.

Когда вы используете этот синтаксис, система с обратной связью, CL представляет ответ от [w 1; w 2; ref] к [z 1; z 2].

Примеры

свернуть все

Скрипт Open Live Script

Следующий код показывает, как ncfsyn может использоваться для формирования цикла. 

s = zpk('s');
G = (s-1)/(s+1)^2;
W1 = 0.5/s; 
[K,CL,GAM] = ncfsyn(G,W1);
sigma(G*K,'r',G*W1,'r-.',G*W1*GAM,'k-.',G*W1/GAM,'k-.')

График сингулярного значения достигнутого цикла G*K равен тому из целевого цикла G*W1 к в плюс или минус GAM (в дБ).

Входные параметры

свернуть все

Объект, заданный как модель динамической системы, такая как модель (ss) пространства состояний. Если G является обобщенной моделью в пространстве состояний с неопределенными или настраиваемыми блоками системы управления, то ncfsyn использует номинальную стоимость или текущее значение тех элементов. G должен иметь то же количество вводов и выводов.

Вес перед компенсатором, заданный как:

  • eye(N) единичной матрицы, где N является количеством вводов или выводов в G.

  • Модель LTI минимальной фазы SISO. В этом случае ncfsyn использует тот же вес для каждого канала цикла.

  • Модель LTI минимальной фазы MIMO тех же размерностей ввода-вывода как G.

Выберите веса предварительного компенсатора и посткомпенсатора W 1 и W 2 таким образом, что усиление имеющего форму объекта Gs = W 2GW1 достаточно высок на частотах, где хорошее затухание воздействия требуется, и достаточно низко на частотах, где хорошая устойчивая устойчивость требуется.

Вес посткомпенсатора, заданный как единичная матрица eye(N) или модель SISO или MIMO LTI. Факторы для определения W2 совпадают с теми для W1.

Выходные аргументы

свернуть все

H ∞-optimal формирующий цикл контроллер, возвращенный как модель (ss) пространства состояний с теми же размерностями ввода-вывода как G. Оптимальный контроллер K = W 1KsW2. См. Алгоритмы.

Оптимальная система с обратной связью от воздействий w 1 и w 2 к выходным параметрам z 1 и z 2, возвращенный как модель в пространстве состояний. Системой с обратной связью дают:

[IK](I−GK)−1[I, G].

H ∞ оптимальная стоимость, возвращенная как значение положительной скалярной величины, больше, чем 1. Оптимальной стоимостью является hinfnorm(CL). Оптимальный контроллер Ks таков, что график сингулярного значения имеющего форму цикла Ls = W 2GW1Ks оптимально совпадает с целевым циклом, формирует Gs к в факторе gamma.

gamma связан с нормированным взаимно-простым запасом устойчивости системы gamma = 1/ncfmargin(Gs,-K). Таким образом gamma дает хорошую индикацию относительно робастности устойчивости к широкому классу неструктурированных изменений объекта со значениями в области значений 1 <gamma <3 соответствия удовлетворительным запасам устойчивости для большинства типичных проектов системы управления.

  • emax — метрика робастности nugap, emax = 1/ gamma (см. gapmetric),

  • Gs — Имеющий форму объект Gs = W 2GW1

  • Ks — Оптимальный контроллер для имеющего форму объекта Gs. Итоговым контроллером является K = W 1KsW2. См. Алгоритмы для деталей.

Советы

  • В то время как ncfmargin принимает цикл отрицательной обратной связи, команда ncfsyn разрабатывает контроллер для цикла позитивных откликов. Поэтому, чтобы вычислить поле с помощью контроллера, разработанного с ncfsyn, используйте [marg,freq] = ncfmargin(G,K,+1).

Алгоритмы

Возвращенный K контроллера = W 1KsW2, где Ks является оптимальный H ∞ контроллер, который минимизирует H ∞ стоимость

γ(Ks)=‖[IKs](I−GsKs)−1[I,Gs]‖∞=‖[IGs](I−KsGs)−1[I,Ks]‖∞.

Оптимальная производительность является минимальной стоимостью

γ:=minKsγ(Ks).

Предположим, что Gs =NM–1, где N (jω) *N (jω) + M (jω) *M (jω) = I, является нормированной взаимно-простой факторизацией (NCF) взвешенной модели объекта управления Gs. Затем теория гарантирует, что система управления остается надежно стабильной для любого возмущения к Gs формы

G˜s=(N+Δ1)(M+Δ2)−1

где Δ1, Δ2 являются стабильным парным удовлетворением

‖[Δ1Δ2]‖∞<MARG:=1γ.

Цель -нормы H с обратной связью имеет стандартную интерпретацию усиления сигнала. Наконец можно показать, что контроллер, Ks, существенно не влияет на форму цикла в частотах, где усиление W 2GW1 или высоко или низко и гарантирует удовлетворительные запасы устойчивости в области частоты перекрестного соединения усиления. В настройке регулятора итоговый контроллер, который будет реализован, является K =W1KsW2.

Смотрите Макфарлэйна и Перчаточника [1] – [2] для деталей.

Ссылки

[1] Макфарлэйн, округ Колумбия и K. Перчаточник, Устойчивое Проектирование контроллера с помощью Нормализованных Взаимно-простых Факторных Описаний Объекта, Springer Verlag, Примечаний Лекции в Управлении и Информатике, издании 138, 1989.

[2] Макфарлэйн, округ Колумбия и K. Перчаточник, “Цикл, Формирующий Методику проектирования с помощью Синтеза”, Транзакции IEEE на Автоматическом управлении, издании 37, № 6, стр 759 - 769, июнь 1992.

[3] Vinnicombe, G., “Измеряя Робастность Систем с обратной связью”, диссертация доктора философии, Отдел Разработки, Кембриджский университет, 1993.

[4] Чжоу, K., и Дж.К. Дойл, основы устойчивого управления. Нью-Йорк: Prentice Hall, 1998.

Смотрите также

| | |

Представлено до R2006a

Документация Robust Control Toolbox
Поддержка