Инвертируйте рекурсию Левинсона-Дербина
r = rlevinson(a,efinal)
[r,u] = rlevinson(a,efinal)
[r,u,k] = rlevinson(a,efinal)
[r,u,k,e] = rlevinson(a,efinal)
Рекурсия Левинсона-Дербина реверса реализует алгоритм понижения для решения следующей симметричной системы Теплица линейных уравнений для r, где r = [r (1) … r (p + 1)] и r (i) * обозначает сопряженное комплексное число r (i).
r = rlevinson(a,efinal) решает вышеупомянутую систему уравнений для r, данного векторный a, где a = [1 a (2) … a (p + 1)]. В приложениях линейного предсказания r представляет последовательность автокорреляции входа к ошибочному фильтру прогноза, где r (1) является элементом нулевой задержки. Фигура ниже показов типичный фильтр этого типа, где H (z) является оптимальным линейным предиктором, x (n), является входным сигналом, предсказанный сигнал, и e (n) является ошибкой прогноза.
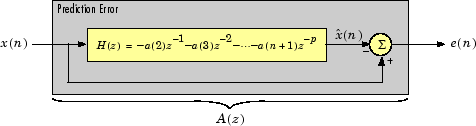
Входной вектор a представляет полиномиальные коэффициенты этой ошибки прогноза, просачивается убывающие степени z.
Фильтр должен быть минимальной фазой, чтобы сгенерировать допустимую последовательность автокорреляции. efinal является скалярной ошибочной степенью прогноза, которая равна отклонению сигнала ошибки прогноза, σ 2 (e).
[r,u] = rlevinson(a,efinal) возвращает верхнюю треугольную матрицу U в разложение UDU*
где
и E является диагональной матрицей с элементами, возвращенными в выводе e (см. ниже). Это разложение разрешает эффективную оценку инверсии матрицы автокорреляции, R −1.
Выходная матрица u содержит полином фильтра прогноза, a, от каждой итерации реверса рекурсия Левинсона-Дербина
где ai (j) является j th коэффициент i th полином фильтра прогноза порядка (т.е. шаг i в рекурсии). Например, 5-й полином фильтра прогноза порядка
a5 = u(5:-1:1,5)'
Обратите внимание на то, что u(p+1:-1:1,p+1)' является входным вектором коэффициентов полинома a.
[r,u,k] = rlevinson(a,efinal) возвращает векторный k длины p + 1 содержащий отражательные коэффициенты. Отражательные коэффициенты являются спряганием значений в первой строке u.
k = conj(u(1,2:end))
[r,u,k,e] = rlevinson(a,efinal) возвращает вектор длины p + 1 содержащий ошибки прогноза от каждой итерации реверса рекурсия Левинсона-Дербина: e(1) является ошибкой прогноза из модели первого порядка, e(2) является ошибкой прогноза из модели второго порядка и так далее.
Эти ошибочные значения прогноза формируют диагональ матричного E в разложении UDU* R −1.
Оцените спектр двух синусоид в шуме с помощью авторегрессивной модели. Выберите лучший порядок модели от группы моделей, возвращенных реверсом рекурсия Левинсона-Дербина.
Сгенерируйте сигнал. Задайте частоту дискретизации 1 кГц и длительность сигнала 50 секунд. Синусоиды имеют частоты 50 Гц и 55 Гц. Шум имеет отклонение 0,2 ².
Fs = 1000; t = (0:50e3-1)'/Fs; x = sin(2*pi*50*t) + sin(2*pi*55*t) + 0.2*randn(50e3,1);
Оцените авторегрессивные параметры модели.
[a,e] = arcov(x,100); [r,u,k] = rlevinson(a,e);
Оцените степень спектральная плотность для порядков 1, 5, 25, 50, и 100.
N = [1 5 25 50 100]; nFFT = 8096; P = zeros(nFFT,5); for idx = 1:numel(N) order = N(idx); ARtest = flipud(u(:,order)); P(:,idx) = 1./abs(fft(ARtest,nFFT)).^2; end
Постройте оценки PSD.
F = (0:1/nFFT:1/2-1/nFFT)*Fs; plot(F, 10*log10(P(1:length(P)/2,:))) grid legend([repmat('Order = ',[5 1]) num2str(N')]) xlabel('Frequency (Hz)') ylabel('dB') xlim([35 70])
[1] Кей, Стивен М. Современная спектральная оценка: теория и приложение. Englewood Cliffs, NJ: Prentice Hall, 1988.
