Односторонний дисперсионный анализ
p = anova1(y)p = anova1(y,group)p = anova1(y,group,displayopt)[p,tbl]
= anova1(___)[p,tbl,stats]
= anova1(___)p = anova1(y)tbl) и диаграмма столбцов y. anova1 тестирует гипотезу, что выборки в y чертятся от населения с тем же средним значением против альтернативной гипотезы, что средние значения генеральной совокупности не являются всеми одинаковыми.
p = anova1(y,group)y группой.
p = anova1(y,group,displayopt)displayopt является 'on' (значение по умолчанию) и подавляет отображения, когда displayopt является 'off'.
[ возвращает структуру, p,tbl,stats]
= anova1(___)stats, который можно использовать, чтобы выполнить тест сравнения кратного. Тест сравнения кратного позволяет вам определить, какие пары средних значений группы существенно отличаются. Чтобы выполнить этот тест, используйте multcompare, обеспечивая структуру stats как входной параметр.
Создайте матрицу выборочных данных y со столбцами, которые являются константами плюс случайные нормальные воздействия со средним значением 0 и стандартным отклонением 1.
y = meshgrid(1:5); rng default; % For reproducibility y = y + normrnd(0,1,5,5)
y = 5×5
1.5377 0.6923 1.6501 3.7950 5.6715
2.8339 1.5664 6.0349 3.8759 3.7925
-1.2588 2.3426 3.7254 5.4897 5.7172
1.8622 5.5784 2.9369 5.4090 6.6302
1.3188 4.7694 3.7147 5.4172 5.4889
Выполните одностороннюю АНОВУ.
p = anova1(y)


p = 0.0023
Таблица АНОВОЙ показывает изменение между группами (Columns) и изменение в группах (Error). SS является суммой квадратов, и df является степенями свободы. Общие степени свободы являются общим количеством наблюдений минус одно, которое равняется 25 - 1 = 24. Степени свободы между группами являются количеством групп минус одна, которая равняется 5 - 1 = 4. Степени свободы в группах являются общими степенями свободы минус между степенями свободы групп, который равняется 24 - 4 = 20.
MS является среднеквадратической ошибкой, которая является SS/df для каждого источника изменения. F-статистическая-величина является отношением среднеквадратических ошибок (13.4309/2.2204). P-значение является вероятностью, что тестовая статистическая величина может принять значение, больше, чем значение вычисленной тестовой статистической величины, т.е. P (F> 6.05). Маленькое p-значение 0,0023 указывает, что различия между средними значениями столбца являются значительными.
Введите выборочные данные.
strength = [82 86 79 83 84 85 86 87 74 82 ... 78 75 76 77 79 79 77 78 82 79]; alloy = {'st','st','st','st','st','st','st','st',... 'al1','al1','al1','al1','al1','al1',... 'al2','al2','al2','al2','al2','al2'};
Данные от исследования силы структурных лучей в Хогге (1987). Векторная сила измеряет отклонения лучей в тысячных частях дюйма менее чем 3 000 фунтов силы. Векторный сплав идентифицирует каждый луч как сталь ('st'), сплавьте 1 ('al1') или сплавьте 2 ('al2'). Несмотря на то, что сплав сортируется в этом примере, группирующие переменные не должны быть отсортированы.
Протестируйте нулевую гипотезу, что стальные балки равны в силе лучам, сделанным из двух более дорогих сплавов. Выключите отображение фигуры и возвратите результаты АНОВОЙ в массиве ячеек.
[p,tbl] = anova1(strength,alloy,'off')p = 1.5264e-04
tbl = 4x6 cell array
Columns 1 through 5
{'Source'} {'SS' } {'df'} {'MS' } {'F' }
{'Groups'} {[184.8000]} {[ 2]} {[ 92.4000]} {[ 15.4000]}
{'Error' } {[102.0000]} {[17]} {[ 6.0000]} {0x0 double}
{'Total' } {[286.8000]} {[19]} {0x0 double} {0x0 double}
Column 6
{'Prob>F' }
{[1.5264e-04]}
{0x0 double }
{0x0 double }
Общие степени свободы являются общим количеством наблюдений минус одно, которое является . Степени свободы между группами являются количеством групп минус одна, которая является . Степени свободы в группах являются общими степенями свободы минус между степенями свободы групп, который является .
MS является среднеквадратической ошибкой, которая является SS/df для каждого источника изменения. F-статистическая-величина является отношением среднеквадратических ошибок. P-значение является вероятностью, что тестовая статистическая величина может принять значение, больше, чем, или равняться значению тестовой статистической величины. P-значение 1.5264e-04 предлагает отклонение нулевой гипотезы.
Можно получить значения в таблице АНОВОЙ путем индексации в массив ячеек. Сохраните значение F-статистической-величины и p-значение в новых переменных Fstat и pvalue.
Fstat = tbl{2,5}Fstat = 15.4000
pvalue = tbl{2,6}pvalue = 1.5264e-04
Введите выборочные данные.
strength = [82 86 79 83 84 85 86 87 74 82 ... 78 75 76 77 79 79 77 78 82 79]; alloy = {'st','st','st','st','st','st','st','st',... 'al1','al1','al1','al1','al1','al1',... 'al2','al2','al2','al2','al2','al2'};
Данные от исследования силы структурных лучей в Хогге (1987). Векторная сила измеряет отклонения лучей в тысячных частях дюйма менее чем 3 000 фунтов силы. Векторный сплав идентифицирует каждый луч как сталь (st), сплавьте 1 (al1) или сплавьте 2 (al2). Несмотря на то, что сплав сортируется в этом примере, группирующие переменные не должны быть отсортированы.
Выполните одностороннюю АНОВУ, использующую anova1. Возвратите структуру stats, который содержит статистику потребности multcompare в выполнении Нескольких Сравнений.
[~,~,stats] = anova1(strength,alloy);


Маленькое p-значение 0,0002 предполагает, что сила лучей не является тем же самым.
Выполните сравнение кратного средней силы лучей.
[c,~,~,gnames] = multcompare(stats);

Отобразите результаты сравнения с соответствующими названиями группы.
[gnames(c(:,1)), gnames(c(:,2)), num2cell(c(:,3:6))]
ans = 3x6 cell array
Columns 1 through 5
{'st' } {'al1'} {[ 3.6064]} {[ 7]} {[10.3936]}
{'st' } {'al2'} {[ 1.6064]} {[ 5]} {[ 8.3936]}
{'al1'} {'al2'} {[-5.6280]} {[-2]} {[ 1.6280]}
Column 6
{[1.6831e-04]}
{[ 0.0040]}
{[ 0.3560]}
Первые два столбца показывают пару групп, которые сравнены. Четвертый столбец показывает различие между предполагаемыми средними значениями группы. Третьи и пятые колонны показывают нижние и верхние пределы для 95% доверительных интервалов истинного различия средних значений. Шестой столбец показывает p-значение для гипотезы, что истинное различие средних значений для соответствующих групп равно нулю.
Первые две строки показывают, что оба сравнения, вовлекающие первую группу (сталь), уверены интервалы, которые не включают нуль. Поскольку соответствующие p-значения (1.6831e-04 и 0.0040, соответственно) являются маленькими, те различия являются значительными.
Третья строка показывает, что различия в силе между двумя сплавами не являются значительными. 95%-й доверительный интервал для различия [-5.6 1.6], таким образом, вы не можете отклонить гипотезу, что истинным различием является нуль. Соответствующее p-значение 0,3560 в шестом столбце подтверждает этот результат.
В фигуре синяя панель представляет интервал сравнения для средней прочности материала для стали. Красные панели представляют интервалы сравнения для средней прочности материала для сплава 1 и сплавляют 2. Ни одна из красных панелей не накладывается с синей панелью, которая указывает, что средняя прочность материала для стали существенно отличается от того из сплава 1 и сплава 2. Подтвердить значительную разницу путем нажатия на панели, которые представляют сплав 1 и 2.
y выборочные данныеВыборочные данные, заданные как вектор или матрица.
Если y является вектором, необходимо задать входной параметр group. group должен быть категориальным переменным, числовым вектором, логическим вектором, символьным массивом, массивом строк или массивом ячеек из символьных векторов, с одним именем для каждого элемента y. Функция anova1 обрабатывает значения y, соответствующие тому же значению group как часть той же группы. Используйте этот проект, когда у групп есть различные числа элементов (разбалансировал АНОВУ).
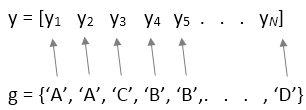
Если y является матрицей, и вы не задаете group, anova1 обрабатывает каждый столбец y как отдельная группа. В этом проекте функция оценивает, равны ли средние значения генеральной совокупности столбцов. Используйте этот проект, когда у каждой группы есть то же число элементов (сбалансировал АНОВУ).
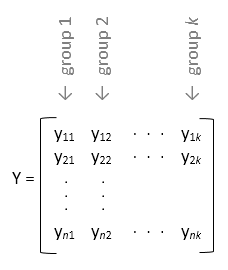
Если y является матрицей, и вы задаете group, то group должен быть символьным массивом, массивом строк или массивом ячеек из символьных векторов, с одним именем для каждого столбца y. Функция anova1 обрабатывает столбцы, которые имеют то же название группы как часть той же группы.
Если group содержит пустой или NaN - оцененные элементы, anova1 игнорирует соответствующие наблюдения в y.
Типы данных: single | double
group — Группирующая переменнаяГруппирующая переменная, заданная как числовой или логический вектор, символьный массив, массив строк или массив ячеек из символьных векторов, содержа названия группы.
Если y является вектором, group должен быть категориальным переменным, числовым вектором, логическим вектором, символьным массивом, массивом строк или массивом ячеек из символьных векторов, с одним именем для каждого элемента y. Функция anova1 обрабатывает значения y, соответствующие тому же значению group как часть той же группы.

N является общим количеством наблюдений.
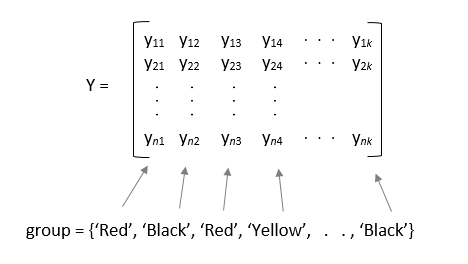
Если y является матрицей, то group должен быть символьным массивом, массивом строк или массивом ячеек из символьных векторов, с одним названием группы для каждого столбца y. Функция anova1 обрабатывает столбцы y, которые имеют то же название группы как часть той же группы.

Если вы не хотите задавать названия группы, введите пустой массив ([]) или не используйте этот аргумент.
Если group содержит пустой или NaN - оцененные элементы, соответствующие наблюдения в y игнорируются.
Для получения дополнительной информации о группирующих переменных смотрите Группирующие переменные.
Например, если y является вектором с наблюдениями, категоризированными в группы 1, 2, и 3, то можно задать группирующие переменные можно следующим образом.
Пример: 'group',[1,2,1,3,1,...,3,1]
Например, если y является матрицей с шестью столбцами, категоризированными в группы, красные, белые, и черные, то можно задать группирующие переменные можно следующим образом.
Пример: 'group',{'white','red','white','black','red'}
Типы данных: single | double | logical | char | string | cell
displayopt — Индикатор, чтобы отобразить таблицу АНОВОЙ и диаграмму'on' (значение по умолчанию) | 'off'Индикатор, чтобы отобразить таблицу АНОВОЙ и диаграмму, заданную как 'on' или 'off'. Когда displayopt является 'off', anova1 возвращает выходные аргументы, только. Это не отображает стандарт таблица АНОВОЙ и коробчатая диаграмма столбцов y.
Пример: p = anova(x,group,'off')
p — p - значение для F - тестp - значение для F - тест, возвращенный как скалярное значение. p - значение является вероятностью, что F - статистическая величина может принять значение, больше, чем вычисленное статистическое тестом значение. anova1 тестирует нулевую гипотезу, что все средние значения группы равны друг другу против альтернативной гипотезы, что по крайней мере одно среднее значение группы отличается от других. Функция выводит p - значение от cdf F - распределение.
Ap-значение, которое меньше, чем уровень значения, указывает, что по крайней мере одно из демонстрационных средних значений существенно отличается от других. Общие уровни значения 0.05 или 0.01.
tbl Таблица АНОВОЙТаблица АНОВОЙ, возвращенная как массив ячеек. tbl имеет шесть столбцов.
| Столбец | Определение |
|---|---|
source | Источник изменчивости. |
SS | Сумма квадратов из-за каждого источника. |
df | Степени свободы сопоставлены с каждым источником. Предположим, что N является общим количеством наблюдений, и k является количеством групп. Затем N – k является степенями свободы в группах (Error), k – 1 является степенями свободы между группами (Columns), и N – 1 является общими степенями свободы. N – 1 = (N – k) + (k – 1) |
MS | Средние квадратичные для каждого источника, который является отношением SS/df. |
F | F-, которая является отношением средних квадратичных. |
Prob>F | p - значение, которое является вероятностью, что F - статистическая величина может принять значение, больше, чем вычисленное статистическое тестом значение. anova1 выводит эту вероятность от cdf F - распределение. |
Строки таблицы show АНОВОЙ изменчивость в данных, которые разделены на источник.
| Строка | Определение |
|---|---|
Groups | Изменчивость из-за различий среди средних значений группы (изменчивость между группами) |
Error | Изменчивость из-за различий между данными в каждой группе и средним значением группы (изменчивость в группах) |
Total | Общая изменчивость |
статистика Статистика для нескольких тестов сравненияСтатистика для нескольких тестов сравнения, возвращенных как структура. stats имеет шесть полей.
| Имя поля | Определение |
|---|---|
gnames | Имена групп |
n | Количество наблюдений в каждой группе |
source | Источник stats вывод |
means | Ориентировочные стоимости средних значений |
df | Степени свободы ошибки (в группах) (N – k, где N является общим количеством наблюдений и k, является количеством групп), |
s | Квадратный корень из среднеквадратической ошибки |
anova1 возвращает диаграммы наблюдений в y группой. Диаграммы обеспечивают визуальное сравнение параметров положения группы.
Если y является вектором, то график показывает одно поле для каждого значения group. Если y является матрицей, и вы не задаете group, то график показывает одно поле для каждого столбца y. На каждом поле центральная метка является медианой, и ребра поля являются 25-ми и 75-ми процентилями (1-е и 3-и квантили). Контактные усики расширяют к самым экстремальным точкам данных, которые не рассматриваются выбросами. Выбросы построены индивидуально. Конечные точки интервала являются экстремальными значениями меток. Экстремальные значения соответствуют q 2 – 1.57 (q 3 – q 1)/sqrt (n) и q 2 + 1.57 (q 3 – q 1)/sqrt (n), где q 2 является медианой (50-я процентиль), q 1 и q 3 является 25-ми и 75-ми процентилями, соответственно, и n является количеством наблюдений без любых значений NaN.
Две медианы существенно отличаются на 5%-м уровне значения, если их интервалы не накладываются. Этот тест отличается от F - тестируют ту АНОВУ, выполняет, но значительные различия в центральных линиях полей соответствуют большому F - статистическим значениям и соответственно маленькому p - значения. Для получения дополнительной информации о диаграммах, смотрите boxplot.
[1] Хогг, R. V., и Дж. Ледолтер. Техническая статистика. Нью-Йорк: Макмиллан, 1987.
anova2 | anovan | boxplot | multcompare
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.