Односторонняя АНОВА

Введение в одностороннюю АНОВУ

Можно использовать функцию Statistics and Machine Learning Toolbox™ anova1, чтобы выполнить односторонний дисперсионный анализ (АНОВА). Цель односторонней АНОВОЙ состоит в том, чтобы определить, имеют ли данные из нескольких групп (уровни) фактора общее среднее значение. Таким образом, односторонняя АНОВА позволяет вам узнать, имеют ли различные группы независимой переменной различные эффекты на переменную отклика y. Предположим, больница хочет определить, предложили ли новые два планировать методы, уменьшают терпеливое время ожидания больше, чем старый способ запланировать назначения. В этом случае независимая переменная является методом планирования, и переменная отклика является временем ожидания пациентов.

Односторонняя АНОВА является простым особым случаем линейной модели. Односторонняя форма АНОВОЙ модели

$y_{i j} = α_{. j} + ε_{i j}$

со следующими предположениями:

y _{i j} является наблюдением, в котором i представляет номер наблюдения и j, представляет другую группу (уровень) переменной прогноза y. Весь _i y _j независим.
α _j представляет среднее значение генеральной совокупности для j th группа (уровень или обработка).
ε _{i j} является случайной ошибкой, независимой и нормально распределенной, с нулевым средним и постоянным отклонением, т.е. ε _{i j} ~ N (0, σ ²).

Эта модель также называется средней моделью. Модель принимает, что столбцами y является постоянный α _j плюс ошибочный компонент ε _{i j}. АНОВА помогает определить, являются ли константы всеми одинаковыми.

АНОВА тестирует гипотезу, что все средние значения группы равны по сравнению с альтернативной гипотезой, что по крайней мере одна группа отличается от других.

$\begin{array}{l} H_{0} : α_{1} = α_{2} = ... = α_{k} \\ H_{1} : не все средние значения группы равны \end{array}$

anova1(y) тестирует равенство средних значений столбца для данных в матричном y, где каждый столбец является другой группой и имеет то же количество наблюдений (т.е. сбалансированный план). anova1(y,group) тестирует равенство средних значений группы, заданных в group, для данных в векторном или матричном y. В этом случае у каждой группы или столбца может быть различное количество наблюдений (т.е. несбалансированный проект).

АНОВА основана на предположении, что все демонстрационное население нормально распределено. Это, как известно, устойчиво к скромным нарушениям этого предположения. Можно проверять предположение нормальности визуально при помощи графика нормальности (normplot). Также можно использовать одну из функций Statistics and Machine Learning Toolbox, которая проверяет на нормальность: Критерий Андерсона-Дарлинга (adtest), тест качества подгонки в квадрате хи (chi2gof), тест Jarque-Bera (jbtest) или тест Lilliefors (lillietest).

Подготовка данных для односторонней АНОВОЙ

Можно обеспечить выборочные данные как вектор или матрицу.

Если выборочные данные находятся в векторе, y, то необходимо предоставить группирующуюся информацию с помощью входной переменной group: anova1(y,group).
group должен быть категориальным переменным, числовым вектором, логическим вектором, символьным массивом, массивом строк или массивом ячеек из символьных векторов, с одним именем для каждого элемента y. Функция anova1 обрабатывает значения y, соответствующие тому же значению group как часть той же группы. Например,

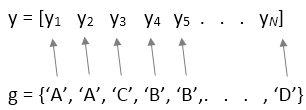
Используйте этот проект, когда у групп есть различные числа элементов (разбалансировал АНОВУ).
Если выборочные данные находятся в матрице, y, предоставляя информацию о группе является дополнительным.
- Если вы не задаете входную переменную group, то anova1 обрабатывает каждый столбец y как отдельная группа и оценивает, равны ли средние значения генеральной совокупности столбцов. Например,
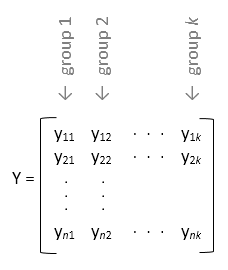
  Используйте эту форму проекта, когда у каждой группы есть то же число элементов (сбалансировал АНОВУ).
- Если вы задаете входную переменную group, то group должен быть символьным массивом, массивом строк или массивом ячеек из символьных векторов, с одним именем для каждого столбца y. Функция anova1 обрабатывает столбцы с тем же названием группы как часть той же группы. Например,

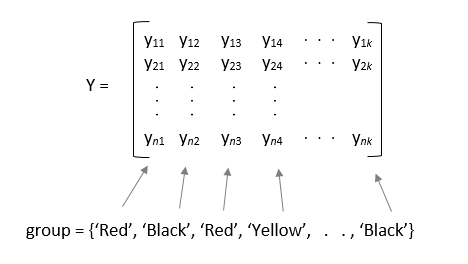
Если group содержит пустой, или NaN оценил элементы, anova1 игнорирует соответствующие наблюдения в y.

Выполните одностороннюю АНОВУ

Скрипт Open Live Script

Этот пример показывает, как выполнить одностороннюю АНОВУ, чтобы определить, имеют ли данные из нескольких групп общее среднее значение.

Загрузите и отобразите выборочные данные.

load hogg
hogg

hogg = 6×5

    24    14    11     7    19
    15     7     9     7    24
    21    12     7     4    19
    27    17    13     7    15
    33    14    12    12    10
    23    16    18    18    20

Данные прибывают от Хогга и Ледолтера (1987) исследование количеств бактерий в поставках молока. Столбцы матричного hogg представляют различные поставки. Строки являются количествами бактерий от коробок молока, выбранного случайным образом из каждой отгрузки.

Протестируйте, если некоторые поставки имеют более высокие количества, чем другие. По умолчанию anova1 возвращает две фигуры. Каждый - стандарт таблица АНОВОЙ, и другой является диаграммами данных группой.

[p,tbl,stats] = anova1(hogg);

p = 1.1971e-04

Маленькое p-значение приблизительно 0,0001 указывает, что количества бактерий от различных поставок не являются тем же самым.

Можно получить некоторое графическое обеспечение, что средние значения отличаются путем рассмотрения диаграмм. Метки, однако, сравнивают медианы, не средние значения. Для получения дополнительной информации об этом отображении смотрите boxplot.

Просмотрите стандарт таблица АНОВОЙ. anova1 сохранил стандарт таблица АНОВОЙ как массив ячеек в выходном аргументе tbl.

tbl

tbl = 4x6 cell array
  Columns 1 through 5

    {'Source' }    {'SS'        }    {'df'}    {'MS'      }    {'F'       }
    {'Columns'}    {[  803.0000]}    {[ 4]}    {[200.7500]}    {[  9.0076]}
    {'Error'  }    {[  557.1667]}    {[25]}    {[ 22.2867]}    {0x0 double}
    {'Total'  }    {[1.3602e+03]}    {[29]}    {0x0 double}    {0x0 double}

  Column 6

    {'Prob>F'    }
    {[1.1971e-04]}
    {0x0 double  }
    {0x0 double  }

Сохраните значение F-статистической-величины в переменной Fstat.

Fstat = tbl{2,5}

Fstat = 9.0076

Просмотрите статистику, необходимую, чтобы сделать кратное попарным сравнением средних значений группы. anova1 сохраняет эти статистические данные в структуре stats.

stats

stats = struct with fields:
    gnames: [5x1 char]
         n: [6 6 6 6 6]
    source: 'anova1'
     means: [23.8333 13.3333 11.6667 9.1667 17.8333]
        df: 25
         s: 4.7209

АНОВА отклоняет нулевую гипотезу, что все средние значения группы равны, таким образом, можно использовать несколько сравнений, чтобы определить, какие средние значения группы отличаются от других. Чтобы провести несколько тестов сравнения, используйте функциональный multcompare, который принимает stats как входной параметр. В этом примере anova1 отклоняет нулевую гипотезу, что средние количества бактерий от всех четырех поставок равны друг другу, т.е. $H_{0} : μ_{1} = μ_{2} = μ_{3} = μ_{4}$ .

Выполните тест сравнения кратного, чтобы определить, какие поставки отличаются, чем другие с точки зрения средних количеств бактерий.

multcompare(stats)

ans = 10×6

    1.0000    2.0000    2.4953   10.5000   18.5047    0.0059
    1.0000    3.0000    4.1619   12.1667   20.1714    0.0013
    1.0000    4.0000    6.6619   14.6667   22.6714    0.0001
    1.0000    5.0000   -2.0047    6.0000   14.0047    0.2119
    2.0000    3.0000   -6.3381    1.6667    9.6714    0.9719
    2.0000    4.0000   -3.8381    4.1667   12.1714    0.5544
    2.0000    5.0000  -12.5047   -4.5000    3.5047    0.4806
    3.0000    4.0000   -5.5047    2.5000   10.5047    0.8876
    3.0000    5.0000  -14.1714   -6.1667    1.8381    0.1905
    4.0000    5.0000  -16.6714   -8.6667   -0.6619    0.0292

Первые два столбца показывают, какие средние значения группы друг по сравнению с другом. Например, первая строка сравнивает средние значения для групп 1 и 2. Последний столбец показывает p-значения для тестов. P-значения 0.0059, 0.0013, и 0.0001 указывают, что средние количества бактерий в молоке от первой отгрузки отличаются от тех от вторых, третьих, и четвертых поставок. P-значение 0,0292 указывает, что средние количества бактерий в молоке от четвертой отгрузки отличаются от тех от пятого. Процедуре не удается отклонить гипотезы, что другие средние значения группы отличаются друг от друга.

Фигура также иллюстрирует тот же результат. Синяя панель показывает интервал сравнения для первого среднего значения группы, которое не накладывается с интервалами сравнения для вторых, третьих, и четвертых средних значений группы, отображенных красным. Интервал сравнения для среднего значения пятой группы, отображенной серым, накладывается с интервалом сравнения для первого среднего значения группы. Следовательно, средние значения группы для первых и пятых групп не существенно отличаются друг от друга.

Математические детали

Тесты АНОВОЙ для различия в группе подразумевают под разделением общего изменения в данных на два компонента:

Изменение группы означает от полного среднего значения, т.е. ${\bar{y}}_{. j} - {\bar{y}}_{..}$ (изменение между группами), где ${\bar{y}}_{. j}$ демонстрационное среднее значение группы j, и ${\bar{y}}_{..}$ полное демонстрационное среднее значение.
Изменение наблюдений в каждой группе от их группы означает оценки, $y_{i j} - {\bar{y}}_{. j}$ (изменение в группе).

Другими словами, АНОВА делит полную сумму квадратов (SST) в сумму квадратов из-за эффекта между группами (SSR) и суммы квадратичных невязок (SSE).

$\underset{S S T}{\underset{︸}{\sum_{i} \sum_{j} {(y_{i j} - {\bar{y}}_{..})}^{2}}} = \underset{S S R}{\underset{︸}{\sum_{j} n_{j} {({\bar{y}}_{. j} - {\bar{y}}_{..})}^{2}}} + \underset{S S E}{\underset{︸}{\sum_{i} \sum_{j} {(y_{i j} - {\bar{y}}_{. j})}^{2}}},$

где _nj является объемом выборки для j th группа, j = 1, 2..., k.

Затем АНОВА сравнивает изменение между группами к изменению в группах. Если отношение изменения в группе к изменению между группами значительно высоко, то можно прийти к заключению, что средние значения группы существенно отличаются друг от друга. Можно измерить это использование тестовой статистической величины, которая имеет F - распределение с (k – 1, N – k) степени свободы:

$F = \frac{\frac{S S R}{k - 1}}{\frac{S S E}{N - k}} = \frac{M S R}{M S E} ~ F_{k - 1, N - k},$

где MSR является среднеквадратической обработкой, MSE является среднеквадратической ошибкой, k является количеством групп, и N является общим количеством наблюдений. Если p - значение для F - статистическая величина меньше, чем уровень значения, то тест отклоняет нулевую гипотезу, что все средние значения группы равны, и приходит к заключению, что по крайней мере одно из средних значений группы отличается от других. Наиболее распространенные уровни значения 0.05 и 0.01.

Таблица АНОВОЙ

Таблица АНОВОЙ получает изменчивость в модели с разбивкой по источникам, F - статистической величине для тестирования значения этой изменчивости и p - значение для выбора значения этой изменчивости. p - значение, возвращенное anova1, зависит от предположений о случайных воздействиях ε _{i j} в образцовом уравнении. Для p - значение, чтобы быть правильными, эти воздействия должны быть независимы, нормально распределены, и иметь постоянное отклонение. Стандарт таблица АНОВОЙ имеет эту форму:

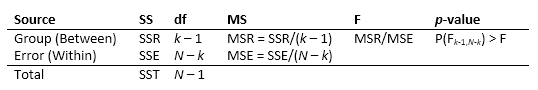
anova1 возвращает стандарт таблица АНОВОЙ как массив ячеек с шестью столбцами.

Столбец	Определение
`Source`	Источник изменчивости.
`SS`	Сумма квадратов из-за каждого источника.
`df`	Степени свободы сопоставлены с каждым источником. Предположим, что N является общим количеством наблюдений, и k является количеством групп. Затем N – k является степенями свободы в группах (`Error`), k – 1 является степенями свободы между группами (`Columns`), и N – 1 является общими степенями свободы: N – 1 = (N – k) + (k – 1).
`MS`	Средние квадратичные для каждого источника, который является отношением `SS/df`.
`F`	F-, которая является отношением средних квадратичных.
`Prob>F`	p - значение, которое является вероятностью, что F - статистическая величина может принять значение, больше, чем вычисленное статистическое тестом значение. `anova1` выводит эту вероятность от cdf F - распределение.

Строки таблицы show АНОВОЙ изменчивость в данных, разделенных на источник.

Строка (Источник)	Определение
`Groups` или `Columns`	Изменчивость из-за различий среди средних значений группы (изменчивость между группами)
`Error`	Изменчивость из-за различий между данными в каждой группе и средним значением группы (изменчивость в группах)
`Total`	Общая изменчивость

Ссылки

[1] Ву, C. F. J. и М. Амада. Эксперименты: планирование, анализ и оптимизация проекта параметра, 2000.

[2] Neter, J., М. Х. Катнер, К. Дж. Нахцхайм и В. Вассерман. 4-й редактор Прикладные Линейные Статистические модели. Ирвин Пресс, 1996.

Документация