Двухсторонняя АНОВА

Введение в двухстороннюю АНОВУ

Можно использовать функцию Statistics and Machine Learning Toolbox™ anova2, чтобы выполнить сбалансированный двухсторонний дисперсионный анализ (АНОВА). Чтобы выполнить двухстороннюю АНОВУ для несбалансированного проекта, используйте anovan. Для примера смотрите Двухстороннюю АНОВУ для Несбалансированного Проекта.

Как в односторонней АНОВОЙ, данные для двухстороннего исследования АНОВОЙ могут быть экспериментальными или наблюдательными. Различие между односторонней и двухсторонней АНОВОЙ - то, что в двухсторонней АНОВОЙ, эффекты двух факторов на переменной отклика представляют интерес. Эти два фактора могут быть независимыми, и не иметь никакого эффекта взаимодействия, или влияние одного фактора на переменной отклика может зависеть от группы (уровень) другого фактора. Если эти два фактора не имеют никаких взаимодействий, модель называется аддитивной моделью.

Предположим, что автомобильная компания имеет две фабрики, и каждая фабрика делает те же три модели автомобилей. Расход бензина в автомобилях может отличаться от фабрики до фабрики и от модели до модели. Эти два фактора, фабрика и модель, объясняют различия в пробеге, то есть, ответе. Одной мерой интереса является различие в пробеге из-за производственных методов между фабриками. Другой мерой интереса является различие в пробеге моделей (независимо от фабрики) из-за различных спецификаций проекта. Эффекты этих мер интереса являются дополнением. Кроме того, предположите, что только одна модель имеет различный расход бензина между фабриками, в то время как пробег других двух моделей является тем же самым между фабриками. Это называется эффектом взаимодействия. Чтобы измерить эффект взаимодействия, должно быть несколько наблюдений для некоторой комбинации модели автомобиля и фабрики. Эти несколько наблюдений называются репликациями.

Двухсторонняя АНОВА является особым случаем линейной модели. Двухсторонняя форма АНОВОЙ модели

$y_{i j r} = μ + α_{i} + β_{j} + {(α β)}_{i j} + ε_{i j r}$

где,

_yijr является наблюдением за переменной отклика.
- i представляет группу i фактора строки A, i = 1, 2..., I
- j представляет группу j фактора столбца B, j = 1, 2..., J
- r представляет номер репликации, r = 1, 2..., R
Существует в общей сложности N = I наблюдения *J*R.
μ является полным средним значением.
_αi является отклонениями групп фактора строки A от полного среднего μ из-за фактора строки B. Значения _αi суммируют к 0.

$\sum_{i = 1}^{I} α_{i} = 0.$
_βj является отклонениями групп в факторе столбца B от полного среднего μ из-за фактора строки B. Все значения в данном столбце _βj идентичны, и значения суммы _βj к 0.

$\sum_{j = 1}^{J} β_{j} = 0.$
_αβij является взаимодействиями. Значения в каждой строке и в каждом столбце _αβij суммируют к 0.

$\sum_{i = 1}^{I} {(α β)}_{i j} = \sum_{j = 1}^{J} {(α β)}_{i j} = 0.$
_εijr является случайными воздействиями. Они приняты, чтобы быть независимыми, нормально распределенными, и иметь постоянное отклонение.

В примере пробега:

_yijr является наблюдениями расхода бензина, μ является полным средним расходом бензина.
_αi является отклонениями экономичности каждого автомобиля от среднего расхода бензина μ из-за модели автомобиля.
_βj является отклонениями экономичности каждого автомобиля от среднего расхода бензина μ из-за фабрики автомобиля.

anova2 требует, чтобы данные были сбалансированы, таким образом, каждая комбинация модели и фабрики должна иметь то же количество автомобилей.

Двухсторонняя АНОВА тестирует гипотезы об эффектах факторов A и B и их взаимодействие на переменной отклика y. Гипотезы о равенстве среднего ответа для групп фактора строки A

$\begin{array}{l} H_{0} : α_{1} = α_{2} \dots = α_{I} \\ H_{1} : по крайней мере один α_{i} отличается, i = 1, 2, ..., I . \end{array}$

Гипотезы о равенстве среднего ответа для групп фактора столбца B

$\begin{array}{l} H_{0} : β_{1} = β_{2} = \dots = β_{J} \\ H_{1} : по крайней мере один β_{j} отличается, j = 1, 2, ..., J . \end{array}$

Гипотезы о взаимодействии столбца и факторов строки

$\begin{array}{l} H_{0} : {(α β)}_{i j} = 0 \\ H_{1} : по крайней мере один {(α β)}_{i j} \neq 0 \end{array}$

Подготовка данных для сбалансированной двухсторонней АНОВОЙ

Чтобы выполнить сбалансированную двухстороннюю АНОВУ, использующую anova2, необходимо расположить данные в определенной матричной форме. Столбцы матрицы должны соответствовать группам фактора столбца, B. Строки должны соответствовать группам фактора строки, A, с тем же количеством репликаций для каждой комбинации групп факторов A и B.

Предположим, что фактор строки, A имеет три группы и фактор столбца B, имеет две группы (уровни). Также предположите, что каждая комбинация факторов A и B имеет два измерения или наблюдения (reps = 2). Затем у каждой группы факторного A есть шесть наблюдений и каждая группа факторного B четыре наблюдения.

$\begin{matrix} \begin{matrix} B = 1 & B = 2 \end{matrix} \\ [\begin{matrix} y_{111} & y_{121} \\ y_{112} & y_{122} \\ y_{211} & y_{221} \\ y_{212} & y_{222} \\ y_{311} & y_{321} \\ y_{312} & y_{322} \end{matrix}] \end{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \end{matrix}} A = 1 \\ \begin{matrix} \end{matrix}} A = 2 \\ \begin{matrix} \end{matrix}} A = 3 \end{matrix} \end{matrix}$

Индексы указывают на строку, столбец и репликацию, соответственно. Например, y ₂₂₁ соответствует измерению для второй группы факторного A, второй группы факторного B и первой репликации для этой комбинации.

Выполните двухстороннюю АНОВУ

Скрипт Open Live Script

Этот пример показывает, как выполнить двухстороннюю АНОВУ, чтобы определить эффект модели автомобиля и фабрики на оценке пробега автомобилей.

Загрузите и отобразите выборочные данные.

load mileage
mileage

mileage = 6×3

   33.3000   34.5000   37.4000
   33.4000   34.8000   36.8000
   32.9000   33.8000   37.6000
   32.6000   33.4000   36.6000
   32.5000   33.7000   37.0000
   33.0000   33.9000   36.7000

Существует три модели автомобилей (столбцы) и две фабрики (строки). Данные имеют шесть строк пробега, потому что каждая фабрика обеспечила три автомобиля каждой модели для исследования (т.е. номер репликации равняется трем). Данные из первой фабрики находятся в первых трех строках, и данные из второй фабрики находятся в последних трех строках.

Выполните двухстороннюю АНОВУ. Возвратите структуру статистики, stats, чтобы использовать в нескольких сравнениях.

nmbcars = 3; % Number of cars from each model, i.e., number of replications
[~,~,stats] = anova2(mileage,nmbcars);

Можно использовать F-статистику, чтобы сделать тесты гипотез, чтобы узнать, является ли пробег тем же самым через модели, фабрики и модель - пары фабрики. Прежде, чем выполнить эти тесты, необходимо настроить для аддитивных эффектов. anova2 возвращает p-значение в эти тесты.

P-значение для образцового эффекта (Columns) является нулем к четырем десятичным разрядам. Этим результатом является верный признак, что пробег отличается от одной модели до другого.

P-значение для эффекта фабрики (Rows) 0.0039, который является также очень значительным. Это значение указывает, что одна фабрика превосходит другой по характеристикам в экономичности автомобилей, которые это производит. Наблюдаемое p-значение указывает, что F-статистическая-величина как экстремальное значение как наблюдаемый F происходит случайно приблизительно четыре из 1 000 раз, если расход бензина был действительно равен от фабрики до фабрики.

Фабрики и модели, кажется, не имеют никакого взаимодействия. P-значение, 0.8411, означает, что наблюдаемый результат вероятен (84 из 100 раз), учитывая, что нет никакого взаимодействия.

Выполните Несколько Сравнений, чтобы узнать, какая пара трех моделей автомобилей существенно отличается.

c = multcompare(stats)

Note: Your model includes an interaction term.  A test of main effects can be 
difficult to interpret when the model includes interactions.

c = 3×6

    1.0000    2.0000   -1.5865   -1.0667   -0.5469    0.0004
    1.0000    3.0000   -4.5865   -4.0667   -3.5469    0.0000
    2.0000    3.0000   -3.5198   -3.0000   -2.4802    0.0000

В матричном c первые два столбца показывают пары моделей автомобилей, которые сравнены. Последний столбец показывает p-значения для теста. Все p-значения являются маленькими (0.0004, 0, и 0), который указывает, что средний пробег всех моделей автомобилей существенно отличается друг от друга.

В фигуре синяя панель является интервалом сравнения для среднего пробега первой модели автомобиля. Красные панели являются интервалами сравнения для среднего пробега вторых и третьих моделей автомобилей. Ни один из вторых и третьих интервалов сравнения не накладывается с первым интервалом сравнения, указывая, что средний пробег первой модели автомобиля отличается от среднего пробега второго и третьих моделей автомобилей. Если вы нажимаете на одну из других панелей, можно протестировать на другие модели автомобилей. Ни одно из перекрытия интервалов сравнения, указывая, что средний пробег каждой модели автомобиля существенно отличается от других двух.

Математические детали

2D фактор АНОВА делит общее изменение на следующие компоненты:

Изменение группы фактора строки означает от полного среднего значения, ${\bar{y}}_{i ..} - {\bar{y}}_{...}$
Изменение группы фактора столбца означает от полного среднего значения, ${\bar{y}}_{. j .} - {\bar{y}}_{...}$
Изменение полного среднего значения плюс репликация означает от среднего значения группы фактора столбца плюс среднее значение группы фактора строки, ${\bar{y}}_{i j .} - {\bar{y}}_{i ..} - {\bar{y}}_{. j .} + {\bar{y}}_{...}$
Изменение наблюдений от средних значений репликации, $y_{i j k} - {\bar{y}}_{i j .}$

АНОВА делит полную сумму квадратов (SST) в сумму квадратов из-за фактора строки A _(SSA), сумма квадратов из-за фактора столбца B _(SSB), сумма квадратов из-за взаимодействия между A и B _(SSAB) и ошибка суммы квадратов (SSE).

$\begin{array}{l} \underset{S S T}{\underset{︸}{\sum_{i = 1}^{m} \sum_{j = 1}^{k} \sum_{r = 1}^{R} {(y_{i j k} - {\bar{y}}_{...})}^{2}}} = \underset{S S_{B}}{\underset{︸}{k R \sum_{i = 1}^{m} {({\bar{y}}_{i ..} - {\bar{y}}_{...})}^{2}}} + \underset{S S_{A}}{\underset{︸}{m R \sum_{j = 1}^{k} {({\bar{y}}_{. j .} - {\bar{y}}_{...})}^{2}}} \\ + \underset{S S_{A B}}{\underset{︸}{R \sum_{i = 1}^{m} \sum_{j = 1}^{k} {({\bar{y}}_{i j .} - {\bar{y}}_{i ..} - {\bar{y}}_{. j .} + {\bar{y}}_{...})}^{2}}} + \underset{S S E}{\underset{︸}{\sum_{i = 1}^{m} \sum_{j = 1}^{k} \sum_{r = 1}^{R} {(y_{i j k} - {\bar{y}}_{i j .})}^{2}}} \end{array}$

АНОВА берет изменение из-за фактора или взаимодействия и сравнивает его с изменением из-за ошибки. Если отношение этих двух изменений высоко, то эффект фактора или эффект взаимодействия являются статистически значительными. Можно измерить статистическое значение с помощью тестовой статистической величины, которая имеет F - распределение.

Для нулевой гипотезы, что средний ответ для групп фактора строки A равен, тестовая статистическая величина

$F = \frac{\frac{S S_{B}}{m - 1}}{\frac{S S E}{m k (R - 1)}} \sim F_{m - 1, m k (R - 1)} .$

Для нулевой гипотезы, что средний ответ для групп фактора столбца B равен, тестовая статистическая величина

$F = \frac{\frac{S S_{A}}{k - 1}}{\frac{S S E}{m k (R - 1)}} \sim F_{k - 1, m k (R - 1)} .$

Для нулевой гипотезы, которую равно нулю взаимодействие столбца и факторов строки, тестовая статистическая величина

$F = \frac{\frac{S S_{A B}}{(m - 1) (k - 1)}}{\frac{S S E}{m k (R - 1)}} \sim F_{(m - 1) (k - 1), m k (R - 1)} .$

Если p - значение для F - статистическая величина меньше, чем уровень значения, то АНОВА отклоняет нулевую гипотезу. Наиболее распространенные уровни значения 0.01 и 0.05.

Таблица АНОВОЙ

Таблица АНОВОЙ получает изменчивость в модели по источнику, F - статистической величине для тестирования значения этой изменчивости и p - значение для выбора значения этой изменчивости. p - значение, возвращенное anova2, зависит от предположений о случайных воздействиях, ε _{i j}, в образцовом уравнении. Для p - значение, чтобы быть правильными, эти воздействия должны быть независимы, нормально распределены, и иметь постоянное отклонение. Стандарт таблица АНОВОЙ имеет эту форму:

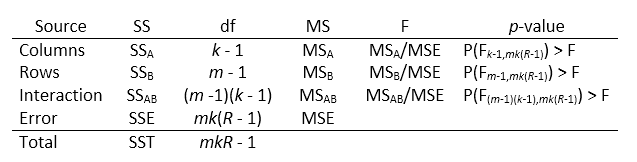
anova2 возвращает стандарт таблица АНОВОЙ как массив ячеек с шестью столбцами.

Столбец	Определение
`Source`	Источник изменчивости.
`SS`	Сумма квадратов из-за каждого источника.
`df`	Степени свободы сопоставлены с каждым источником. Предположим, что J является количеством групп в факторе столбца, I является количеством групп в факторе строки, и R является количеством репликаций. Затем общим количеством наблюдений является IJR, и общие степени свободы IJR – 1. I – 1 является степенями свободы для фактора строки, J – 1 является степенями свободы для фактора столбца, (I – 1) (J – 1) степени свободы взаимодействия, и IJ (R – 1) является ошибочными степенями свободы.
`MS`	Средние квадратичные для каждого источника, который является отношением `SS/df`.
`F`	F-, которая является отношением средних квадратичных.
`Prob>F`	p - значение, которое является вероятностью, что F - статистическая величина может принять значение, больше, чем вычисленное статистическое тестом значение. `anova2` выводит эту вероятность от cdf F - распределение.

Строки таблицы show АНОВОЙ изменчивость в данных, которые разделены на источник.

Строка (Источник)	Определение
`Columns`	Изменчивость из-за фактора столбца
`Rows`	Изменчивость из-за фактора строки
`Interaction`	Изменчивость из-за взаимодействия факторов строки и столбца
`Error`	Изменчивость из-за различий между данными в каждой группе и средним значением группы (изменчивость в группах)
`Total`	Общая изменчивость

Ссылки

[1] Ву, C. F. J. и М. Амада. Эксперименты: планирование, анализ и оптимизация проекта параметра, 2000.

[2] Neter, J., М. Х. Катнер, К. Дж. Нахцхайм и В. Вассерман. 4-й редактор Прикладные Линейные Статистические модели. Ирвин Пресс, 1996.

Связанные примеры

Двухсторонняя АНОВА для несбалансированного проекта

Документация