densematrixСоздайте матрицу или вектор
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
densematrix(Array) densematrix(List) densematrix(ListOfRows) densematrix(Matrix) densematrix(m,n) densematrix(m,n,Array) densematrix(m,n,List) densematrix(m,n,ListOfRows) densematrix(m,n,f) densematrix(m,n,List, Diagonal) densematrix(m,n,g, Diagonal) densematrix(m,n,List, Banded) densematrix(1,n,Array) densematrix(1,n,List) densematrix(m,1,Array) densematrix(m,1,List)
densematrix(m, n, [[a11, a12, ...], [a21, a22, ...], ...]) возвращает m ×n матрица
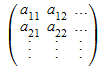 .
.
densematrix(n, 1, [a1, a2, ...]) возвращает n ×1 вектор-столбец
 .
.
densematrix(1, n, [a1, a2, ...]) возвращается 1×n вектор - строка
![]() .
.
densematrix создает матрицы и векторы. Вектором с записями n является любой n ×1 матрица (вектор-столбец) или 1×n матрица (вектор - строка).
Матричные и векторные компоненты должны быть арифметическими выражениями. Для определенных областей компонента обратитесь к странице справки Dom::DenseMatrix.
Арифметические операции с матрицами могут быть выполнены при помощи стандартных арифметических операторов MuPAD®.
Например, если A и B являются двумя матрицами, заданными densematrix, то A + B вычисляет сумму, и A * B вычисляет продукт этих двух матриц, при условии, что размерности правильны.
Точно так же A^(-1) или 1/A вычисляют инверсию квадратной матрицы A, если это существует. В противном случае FAIL возвращен.
Смотрите пример 1.
Много системных функций принимают, что матрицы как вход, такие как map, subs, has, zip, conjugate вычисляют сопряженное комплексное число матрицы, norm, чтобы вычислить матричные нормы, или даже exp, чтобы вычислить экспоненциал матрицы. Смотрите Пример 4.
Большинство функций в пакете линейной алгебры MuPAD linalg работает с матрицами. Например, команда linalg::gaussJordan(A) выполняет Исключение по Гауссу-Жордану на A, чтобы преобразовать A к его приведенному ступенчатому по строкам виду матрицы. Смотрите Пример 2.
Смотрите страницу справки linalg для списка доступных функций этого пакета.
densematrix является сокращением от доменного Dom::DenseMatrix (). Вы находите больше информации об этом типе данных для матриц на соответствующей странице справки.
Матричные компоненты могут быть извлечены обычным индексным оператором [ ], который также работает на списки, массивы, hfarrays, и таблицы. Вызов A[i, j] извлекает матричный компонент в i th строка и j th столбец.
Присвоения на матричные компоненты выполняются так же. Вызов A[i, j] := c заменяет матричный компонент в i th строка и j th столбец A c.
Если один из индексов не находится в его допустимой области значений, то сообщение об ошибке выпущено.
Индексный оператор также извлекает подматрицы. Вызов A[r1..r2, c1..c2] создает субматрицу A, включающего строки с индексами r 1, r 1 + 1, …, r 2 и столбцы с индексами c 1, c 1 + 1, …, c 2 из A.
densematrix(Array) или densematrix(Matrix) создают новую матрицу с той же размерностью и компонентами Array или Matrix, соответственно. Массив не должен содержать неинициализированные записи. Если Array одномерен, то результатом является вектор-столбец. Cf. Пример 7.
densematrix(List) создает m ×1 вектор-столбец с компонентами, взятыми из непустого списка, где m является количеством записей List. Смотрите Пример 5.
densematrix(ListOfRows) создает m ×n матрица с компонентами, взятыми из вложенного listListOfRows, где m является количеством внутренних списков ListOfRows, и n является максимальным числом элементов внутреннего списка. Каждый внутренний список соответствует строке матрицы. И m и n должны быть ненулевыми.
Если внутренний список имеет меньше, чем записи n, то остающиеся компоненты в соответствующей строке матрицы обнуляются. Смотрите Пример 6.
Это может быть хорошая идея сначала, чтобы создать двумерный массив из того списка прежде, чем вызвать densematrix. Это - то, вследствие того, что создание матрицы от массива является самым быстрым способом, которым можно достигнуть. Однако в этом случае подсписки должны иметь то же число элементов.
Вызов densematrix(m, n) возвращает m ×n нулевая матрица.
densematrix(m, n, Array) вызова создает m ×n матрица с компонентами, взятыми из Array, который должен быть массивом или hfarray. Array должен иметь m n операнды. Первые операнды m задают первую строку, следующие операнды m задают вторую строку и т.д. Форматирование массива не важно. Например, любой массив с 6 элементами может использоваться, чтобы создать матрицы размерности 1 ×6, или 2×3, или 3×2, или 6 ×1.
densematrix(m, n, List) создает m ×n матрица с компонентами взятая строка после строки из непустого списка. Список должен содержать m n записи. Cf. Пример 6.
densematrix(m, n, ListOfRows) создает m ×n матрица с компонентами, взятыми из списка ListOfRows.
Если m ≥ 2 и n ≥ 2, то ListOfRows должен состоять из в большей части m внутренние списки, каждый имеющий при большинстве записей n. Внутренние списки соответствуют строкам возвращенной матрицы.
Если внутренний список имеет меньше, чем записи n, то остающиеся компоненты соответствующей строки матрицы обнуляются. Если существуют меньше, чем m внутренние списки, то остающиеся более низкие строки матрицы заполнены, обнуляет. Смотрите Пример 6.
densematrix(m, n, f) возвращает матрицу, чья (i, j) th компонент f(i,j). Индекс строки i запускается от 1 до m и индекса столбца j от 1 до n. Смотрите Пример 8.
densematrix(m, 1, Array) возвращает m ×1 вектор-столбец с компонентами, взятыми из Array. array или hfarray Array должны иметь записи m.
densematrix(m, 1, List) возвращает m ×1 вектор-столбец с компонентами, взятыми из List. Список List должен иметь при большинстве записей m. Если существует меньше записей, то остающиеся векторные компоненты обнуляются. Смотрите Пример 5.
densematrix(1, n, Array) возвращает 1 ×n вектор - строку с компонентами, взятыми из Array. array или hfarray Array должны иметь записи n.
densematrix(1, n, List) возвращает 1 ×n вектор - строку с компонентами, взятыми из List. Список List должен иметь при большинстве записей n. Если существует меньше записей, то остающиеся векторные компоненты обнуляются. Смотрите Пример 5.
Компоненты матрицы больше не оцениваются после создания матрицы, т.е. если они содержат свободные идентификаторы, они не будут заменены их значениями.
Мы создаем 2×2 матрица
![]()
путем передачи списка двух строк к densematrix, где каждая строка является списком двух элементов, можно следующим образом:
A := densematrix([[1, 5], [2, 3]])
![]()
Таким же образом мы генерируем следующие 2 ×3 матрицы:
B := densematrix([[-1, 5/2, 3], [1/3, 0, 2/5]])

Мы можем сделать матричную арифметику с помощью стандартных арифметических операторов MuPAD. Например, матричным произведением A B, 4-я степень A и скалярное умножение A![]() дают:
дают:
A * B, A^4, 1/3 * A

Начиная с размерностей матриц отличаются A и B, сумма A и B не задана, и MuPAD возвращает сообщение об ошибке:
A + B
Error: Dimensions do not match. [(Dom::DenseMatrix(Dom::ExpressionField()))::_plus]
Вычислить инверсию A, введите:
1/A
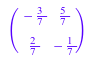
Если матрица не является обратимой, то результатом этой операции является FAIL:
C := densematrix([[2, 0], [0, 0]])
![]()
C^(-1)
![]()
В дополнение к стандартной матричной арифметике библиотека linalg предлагает много функций, обрабатывающих матрицы. Например, функциональный linalg::rank определяет ранг матрицы:
A := densematrix([[1, 5], [2, 3]])
![]()
linalg::rank(A)
![]()
Функциональный linalg::eigenvectors вычисляет собственные значения и собственные вектора A:
linalg::eigenvectors(A)

Чтобы определить размерность матрицы используют функциональный linalg::matdim:
linalg::matdim(A)
![]()
Результатом является список двух положительных целых чисел, количество строки и столбца матрицы.
Используйте info(linalg), чтобы получить список доступных функций или ввести ?linalg для получения дополнительной информации об этой библиотеке.
К матричным записям можно получить доступ с индексным оператором [ ]:
A := densematrix([[1, 2, 3, 4], [2, 0, 4, 1], [-1, 0, 5, 2]])

A[2, 1] * A[1, 2] - A[3, 1] * A[1, 3]
![]()
Можно переопределить матричную запись путем присвоения значения ему:
A[1, 2] := a^2: A

Индексный оператор может также использоваться, чтобы извлечь подматрицы. Следующий вызов создает копию субматрицы A, включающего второе и третью строку и первые три столбца A:
A[2..3, 1..3]
![]()
Индексный оператор не позволяет заменять субматрицу данной матрицы другой матрицей. Используйте linalg::substitute, чтобы достигнуть этого.
Некоторые системные функции могут быть применены к матрицам. Например, если вы имеете матрицу с символьными записями и хотите иметь все записи в расширенной форме, просто применить функциональный expand:
delete a, b: A := densematrix([ [(a - b)^2, a^2 + b^2], [a^2 + b^2, (a - b)*(a + b)] ])

expand(A)

Можно дифференцировать все матричные компоненты относительно некоторых неопределенных:
diff(A, a)
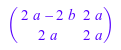
Следующая команда оценивает все матричные компоненты в данной точке:
subs(A, a = 1, b = -1)
![]()
Обратите внимание на то, что функциональный subs не оценивает результат замены. Например, мы задаем следующую матрицу:
A := densematrix([[sin(x), x], [x, cos(x)]])

Затем мы заменяем x = 0 в каждом матричном компоненте:
B := subs(A, x = 0)

Вы видите, что матричные компоненты не оценены полностью: например, если вы вводите sin(0) непосредственно, он оценивает, чтобы обнулить.
Функциональный eval может использоваться, чтобы оценить результат функционального subs. Однако eval не работает с матрицами непосредственно, и необходимо использовать функциональный map, чтобы применить функциональный eval к каждому матричному компоненту:
map(B, eval)
![]()
Функциональный zip может быть применен к матрицам. Следующий вызов комбинирует две матрицы A и B путем деления каждого компонента A соответствующим компонентом B:
A := densematrix([[4, 2], [9, 3]]): B := densematrix([[2, 1], [3, -1]]): zip(A, B, `/`)
![]()
Вектором является любой m ×1 матрица (вектор-столбец) или 1×n матрица (вектор - строка). Чтобы создать вектор с densematrix, передайте размерность вектора и список векторных компонентов в качестве аргумента к densematrix:
row_vector := densematrix(1, 3, [1, 2, 3]); column_vector := densematrix(3, 1, [1, 2, 3])
![]()
![]()
Если единственный аргумент densematrix является невложенным списком или одномерным массивом, то результатом является вектор-столбец:
densematrix([1, 2, 3])
![]()
Для вектора - строки r вызовы r[1, i] и r[i] оба возвращают i th векторный компонент r. Точно так же для вектор-столбца c, вызовы c[i, 1] и c[i] оба возвращают i th векторный компонент c.
Например, чтобы извлечь второй компонент векторов row_vector и column_vector, мы входим:
row_vector[2], column_vector[2]
![]()
Используйте функциональный linalg::vecdim, чтобы определить количество компонентов вектора:
linalg::vecdim(row_vector), linalg::vecdim(column_vector)
![]()
Количество компонентов вектора может также быть определено непосредственно вызовом nops(vector).
Размерность вектора может быть определена, как описано выше в случае матриц:
linalg::matdim(row_vector), linalg::matdim(column_vector)
![]()
Смотрите linalg пакет для функций, работающих с векторами и страницей справки norm для вычислительных векторных норм.
В следующих примерах мы иллюстрируем различные вызовы densematrix, как описано выше. Мы запускаем путем передачи вложенного списка densematrix, где каждый внутренний список соответствует строке матрицы:
densematrix([[1, 2], [2]])
![]()
Количество строк созданной матрицы является количеством внутренних списков, а именно, m = 2. Количество столбцов определяется максимальным количеством записей внутреннего списка. В примере выше, первый список является самым длинным, и следовательно n = 2. Второй список имеет только один элемент, и поэтому вторая запись во второй строке возвращенной матрицы была обнулена.
В следующем вызове мы используем тот же вложенный список, но кроме того передаем два параметра размерности, чтобы создать 4×4 матрица:
densematrix(4, 4, [[1, 2], [2]])

В этом случае размерность матрицы дана параметрами размерности. Как прежде, недостающие записи во внутреннем списке соответствуют нулю, и кроме того недостающие строки обработаны как нулевые строки.
Если размерность, m ×n матрицы утверждается явным образом, записи, может также быть задана простым списком с m n элементы. Матрица заполнена этими элементами строка строкой:
densematrix(2, 3, [1, 2, 3, 4, 5, 6])
![]()
densematrix(3, 2, [1, 2, 3, 4, 5, 6])

Один - или двумерный массив арифметических выражений, таких как:
a := array(1..3, 2..4, [[ 1, 1/3 , 0 ],
[-2, 3/5 , 1/2],
[-3/2, 0 , -1 ]])
может быть преобразован в матрицу можно следующим образом:
A := densematrix(a)

Подача массивов, например, как эффективный структурированный тип данных для программирования. Однако массивы не имеют никакого алгебраического значения, и никакие математические операции не заданы для них. Если вы преобразовываете массив в матрицу, можно использовать полную функциональность, заданную для матриц, как описано выше. Например, давайте вычислим матрицу 2 A - A 2 и норма Фробениуса A:
2*A - A^2, norm(A, Frobenius)
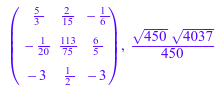
Обратите внимание на то, что массив может содержать неинициализированные записи:
b := array(1..4): b[1] := 2: b[4] := 0: b
![]()
densematrix не может обработать массивы, которые имеют неинициализированные записи, и отвечает сообщением об ошибке:
densematrix(b)
Error: Unable to define a matrix over 'Dom::ExpressionField()'. [(Dom::DenseMatrix(Dom::ExpressionField()))::new]
Мы инициализируем остающиеся записи массива b и преобразовываем его в матрицу, или более точно, в вектор-столбец:
b[2] := 0: b[3] := -1: densematrix(b)

Мы показываем, как создать матрицу, компоненты которой заданы функцией строки и индекса столбца. Запись в i th строка и j th столбец Гильбертовой матрицы (см. также linalg::hilbert)![]() . Таким образом следующая команда создает 2×2 Гильбертова матрица:
. Таким образом следующая команда создает 2×2 Гильбертова матрица:
densematrix(2, 2, (i, j) -> 1/(i + j - 1))
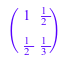
Следующие два вызова приводят к различным результатам. В первом вызове x рассматривается как неизвестная функция, в то время как это - константа во втором вызове:
delete x: densematrix(2, 2, x), densematrix(2, 2, (i, j) -> x)

Диагональные матрицы могут быть созданы путем передачи опции Diagonal и список диагональных элементов:
densematrix(3, 4, [1, 2, 3], Diagonal)

Следовательно, можно сгенерировать 3×3 единичная матрица можно следующим образом:
densematrix(3, 3, [1 $ 3], Diagonal)

Эквивалентно, можно использовать функцию одного аргумента:
densematrix(3, 3, i -> 1, Diagonal)
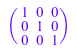
Поскольку целочисленный 1 также представляет постоянную функцию, следующий более короткий вызов создает ту же матрицу:
densematrix(3, 3, 1, Diagonal)
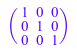
Полосные матрицы Теплица (см. выше) могут быть созданы с опцией Banded. Следующая команда создает матрицу пропускной способности 3 со всеми основными диагональными элементами, равными 2 и все записи на первом под - и супердиагонали, равной - 1:
densematrix(4, 4, [-1, 2, -1], Banded)

|
Один - или двумерный массив типа |
| |
|
Вложенный список строк, каждая строка, являющаяся списком арифметических выражений |
|
Матрица, т.е. объект типа данных категории |
|
Количество строк: положительное целое число |
|
Количество столбцов: положительное целое число |
|
Функция или функциональное выражение двух аргументов |
|
Функция или функциональное выражение одного аргумента |
|
Создайте диагональную матрицу С опцией
|
|
Создайте полосную матрицу Теплица Ленточная матрица имеет весь нуль записей вне основной диагонали и некоторые смежные под - и супердиагоналей.
Все элементы основной диагонали созданной матрицы инициализируются со средним элементом Смотрите пример 10. |
Матрица доменный типDom::DenseMatrix().