Dom:: DenseMatrix
Синтаксис
Доменное создание
Dom::DenseMatrix(<R>)
Создание элемента
Dom::DenseMatrix(R)(Array)
Dom::DenseMatrix(R)(List)
Dom::DenseMatrix(R)(ListOfRows)
Dom::DenseMatrix(R)(Matrix)
Dom::DenseMatrix(R)(m, n)
Dom::DenseMatrix(R)(m, n, Array)
Dom::DenseMatrix(R)(m, n, List)
Dom::DenseMatrix(R)(m, n, ListOfRows)
Dom::DenseMatrix(R)(m, n, f)
Dom::DenseMatrix(R)(m, n, List, Diagonal)
Dom::DenseMatrix(R)(m, n, g, Diagonal)
Dom::DenseMatrix(R)(m, n, List, Banded)
Dom::DenseMatrix(R)(1, n, List)
Dom::DenseMatrix(R)(m, 1, List)
Описание
Доменное создание
Dom::DenseMatrix(R) создает области матриц по доменному R компонента категории Cat::Rng (звонок, возможно без модуля).
Если дополнительный параметр, который R не дан, доменный Dom::ExpressionField(), используется.
Вектором с записями n является любой n ×1 матрица (вектор-столбец), или 1×n матрица (вектор - строка).
Арифметические операции с матрицами могут быть выполнены при помощи стандартных арифметических операторов MuPAD®.
Например, если A и B являются двумя матрицами, заданными Dom::DenseMatrix(R), A + B вычисляет сумму, и A * B вычисляет продукт этих двух матриц, при условии, что размерности правильны.
Точно так же A^(-1) или 1/A вычисляют инверсию квадратной матрицы A, если это существует и возвращает FAIL в противном случае. Смотрите Пример 1.
Много системных функций были перегружены для матриц, таких как map, subs, has, zip, conjugate, чтобы вычислить сопряженное комплексное число матрицы, norm, чтобы вычислить матричные нормы или exp, чтобы вычислить экспоненциал матрицы.
Большинство функций в пакете линейной алгебры MuPAD linalg работает с матрицами. Например, команда linalg::gaussJordan(A) выполняет Исключение по Гауссу-Жордану на A, чтобы преобразовать A к его приведенному ступенчатому по строкам виду матрицы.
Доменный Dom::DenseMatrix(R) представляет матрицы по R произвольного размера, и это поэтому не имеет никакой алгебраической структуры (кроме того, чтобы быть набором матриц).
Доменный Dom::SquareMatrix(n, R) представляет звонок n ×n матрицы по R. Доменный Dom::MatrixGroup(m, n, R) представляет Абелевую группу m ×n матрицы по R.
Мы используем следующие обозначения для матричного A (элемент Dom::DenseMatrix(R)):
nrows (A) обозначает количество строк A.
ncols (A) обозначает количество столбцов A.
Индекс строки является целым числом в диапазоне от 1 до nrows (A).
Индекс столбца является целым числом в диапазоне от 1 до ncols (A).
Примечание
Компоненты матрицы больше не оцениваются после создания матрицы, т.е. если они содержат свободные идентификаторы, они не будут заменены их значениями.
Создание элемента
Dom::DenseMatrix(R)(Array) и Dom::DenseMatrix(R)(Matrix) создают новую матрицу с размерностью и компонентами Array и Matrix, соответственно.
Компоненты Array или Matrix преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.
Dom::DenseMatrix(R)(List) создает m ×1 вектор-столбец с компонентами, взятыми из непустого списка, где m является количеством записей List.
Dom::DenseMatrix(R)(ListOfRows) создает m ×n матрица с компонентами, взятыми из вложенного списка ListOfRows, где m является количеством внутренних списков ListOfRows, и n является максимальным числом элементов внутреннего списка. Каждый внутренний список соответствует строке матрицы. И m и n должны быть ненулевыми.
Если внутренний список имеет меньше, чем записи n, то остающиеся компоненты в соответствующей строке матрицы обнуляются.
Записи внутренних списков преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.
Это может быть хорошая идея сначала, чтобы создать двумерный массив из того списка прежде, чем вызвать Dom::DenseMatrix(R). Это - то, вследствие того, что создание матрицы от массива является самым быстрым способом, которым можно достигнуть. Однако в этом случае подсписки должны иметь то же число элементов.
Вызов Dom::DenseMatrix(R)(m, n) возвращает m ×n нулевая матрица.
Используйте метод "identity", чтобы создать n ×n единичная матрица.
Dom::DenseMatrix(R)(m, n, Array) вызова создает m ×n матрица с компонентами, взятыми из Array, который должен быть массивом или hfarray. Array должен иметь m n операнды. Первые операнды m задают первую строку, следующие операнды m задают вторую строку и т.д. Форматирование массива не важно. Например, любой массив с 6 элементами может использоваться, чтобы создать матрицу размерности 1 ×6, или 2×3, или 3×2, или 6 ×1.
Вызов Dom::DenseMatrix(R)(m, n, List) создает m ×n матрица с компонентами, взятыми из списка List с m n элементы. Первые элементы m списка задают первую строку, следующие элементы m списка задают вторую строку и т.д.
Вызов Dom::DenseMatrix(R)(m, n, ListOfRows) создает m ×n матрица с компонентами, взятыми из listListOfRows.
Если m ≥ 2 и n ≥ 2, то ListOfRows должен состоять из в большей части m внутренние списки, каждый имеющий при большинстве записей n. Внутренние списки соответствуют строкам возвращенной матрицы.
Если внутренний список имеет меньше, чем записи n, то остающиеся компоненты соответствующей строки матрицы обнуляются. Если существуют меньше, чем m внутренние списки, то остающиеся более низкие строки матрицы заполнены, обнуляет.
Dom::DenseMatrix(R)(m, n, f) возвращает матрицу, чья (i, j) th компонент значение вызова функции f(i,j). Индекс строки i колеблется от 1 до m и индекса столбца j от 1 до n.
Значения функции преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.
Dom::DenseMatrix(R)(1, n, List) возвращает 1 ×n вектор - строку с компонентами, взятыми из List. Список List должен иметь при большинстве записей n. Если существует меньше записей, то остающиеся векторные компоненты обнуляются.
Записи списка преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.
Dom::DenseMatrix(R)(m, 1, List) возвращает m ×1 вектор-столбец с компонентами, взятыми из List. Список List должен иметь при большинстве записей m. Если существует меньше записей, то остающиеся векторные компоненты обнуляются.
Записи списка преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.
Примеры
Пример 1
Сначала мы создаем область матриц по полю рациональных чисел:
Мы присвоили эту область идентификатору MatQ. Затем мы задаем 2×2 матрица
списком двух строк, где каждая строка является списком двух элементов:
Таким же образом мы задаем следующие 2 ×3 матрицы:
и выполните матричную арифметику с помощью стандартных арифметических операторов MuPAD, например, матричное произведение A B, 4-я степень A, а также скалярное умножение времен A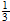 :
:
Матрицы A и B имеют различные размерности, и поэтому сумму A и B, не заданы. MuPAD выдает ошибку сообщение:
Error: Dimensions do not match. [(Dom::DenseMatrix(Dom::Rational))::_plus]
Чтобы вычислить инверсию A, только войдите:
Если матрица не является обратимой, FAIL является результатом этой операции. Например, матрица:
не является обратимым, следовательно:
Пример 2
Мы создаем область матриц по реалам:
Около стандартной матричной арифметики библиотека linalg предлагает много функций, имеющих дело с матрицами. Например, если вы хотите вычислить ранг матрицы, используйте linalg::rank:
Используйте linalg::eigenvectors, чтобы вычислить собственные значения и собственные вектора матричного A:
Попробуйте info(linalg) за список доступных функций или введите help(linalg) для получения дополнительной информации о библиотеке linalg.
Некоторые функции в пакете linalg просто служат “интерфейсными” функциями для методов матричной области, описанной выше. Например, linalg::transpose использует метод "transpose", чтобы получить транспонированную матрицу. Функциональный linalg::gaussElim применяет Исключение Гаусса к матрице, такой как:
Вычисление выполняется методом "gaussElim", как описано выше. Такие функции пакетов linalg, в отличие от соответствующих методов доменного Dom::DenseMatrix(R), проверяют свои входящие параметры, и некоторые из них предлагают расширенные функциональности.
Пример 3
В этом примере мы используем матричную область по умолчанию, которая создается Dom::DenseMatrix(). Эта область представляет матрицы, компоненты которых могут быть произвольными арифметическими выражениями (т.е. звонком компонента является доменный Dom::ExpressionField ()).
Эта область уже известна MuPAD именем matrix:
Матричные компоненты могут быть извлечены индексным оператором []:
Если один из индексов не находится в его допустимой области значений, сообщение об ошибке выпущено. Присвоения на матричные компоненты выполняются так же:
Около обычной индексации матричных компонентов также возможно извлечь подматрицы из данной матрицы. Следующий вызов создает субматрицу A, который состоит из строк 2 - 3 и столбцов 1 - 3 A:
Индексный оператор не позволяет вставлять подматрицы в данную матрицу. Это реализовано функциональным linalg::substitute.
Пример 4
В следующих примерах мы демонстрируем различные способы создать матрицы. Мы работаем с матрицами, заданными по полю ℤ 19, т.е. полю целых чисел по модулю 19. Этот звонок компонента может быть создан с доменным конструктором Dom::IntegerMod.
Мы запускаем путем предоставления списка строк, где каждая строка является списком записей строки:
Элементы двух внутренних списков, записей строки, были преобразованы в элементы доменного Dom::IntegerMod(19).
Количество строк является количеством подсписков аргумента, т.е. m = 2. Количество столбцов определяется длиной внутреннего списка с большинством записей, который является первым внутренним списком с двумя записями. Недостающие записи в других внутренних списках обработаны как нулевые компоненты. Вызов:
фиксирует размерность матрицы. Недостающие записи и внутренние списки обработаны как нулевые компоненты и обнуляют строки, соответственно.
Сообщение об ошибке выпущено, если одна из данных записей не может быть преобразована в элемент по ℤ 19:
Error: Unable to define a matrix over 'Dom::IntegerMod(19)'. [(Dom::DenseMatrix(Dom::IntegerMod(19)))::new]
Пример 5
Этот пример иллюстрирует, как создать матрицу с компонентами, данными как значения индексной функции. Сначала мы создаем 2 ×2 Гильбертовых матрицы (см. также функции linalg::hilbert и linalg::invhilbert):
Отметьте различие при работе с выражениями и функциями. Если вы даете выражение, оно обработано как функция в индексах строки и столбца:
Пример 6
Диагональные матрицы могут быть созданы с опцией Diagonal и список диагональных компонентов:
Следовательно, чтобы задать n ×n единичная матрица, можно войти:
или даже вызов:
Самый легкий способ создать единичную матрицу, однако, состоит в том, чтобы использовать метод "identity":
Пример 7
Матрицы Теплица могут быть заданы с опцией Banded. Следующий вызов задает три ленточных матрицы с 2 компонента на основной диагонали и компоненте - 1 на первых поддиагоналях:
Пример 8
Некоторые системные функции могут быть применены к матрицам, таким как norm, expand, diff, conjugate или exp.
Например, чтобы расширить компоненты матрицы:
войдите:
Если вы хотите дифференцировать матричные компоненты, то вызовите, например:
Заменять матричными компонентами некоторыми значениями, введите:
Функциональный zip может также быть применен к матрицам. Следующий вызов комбинирует две матрицы A и B путем деления каждого компонента A соответствующим компонентом B:
Заключенный в кавычки символьный `/` является другим обозначением для функционального _divide, функциональной формы оператора деления /.
Если нужно применить функцию к компонентам матрицы, то используйте функциональный map. Например, чтобы упростить компоненты матрицы:
вызов:
Пример 9
Однако там может появиться некоторые неожиданные результаты с помощью функционального diff в контексте матриц. Производная следующего незаданного функционального f матрицы вычисляется из-за цепочечного правила:
Обычно, функциональный f был бы неявно принят, чтобы быть скаляром. Следовательно, производная f должна быть скаляром также. В вышеупомянутой ситуации цепочечное правило применяется для дифференцирования: внутренняя функция является матрицей, содержащей символьные компоненты a*x^2, b, c и d. Его производная вычисляется путем простого применения diff к каждому компоненту матрицы:
Наконец, внешний незаданный функциональный f неявно принят, чтобы быть скаляром, таким, что каждый компонент производной внутренней функции умножается на внешнее дифференцирование.
Пример 10
Вектор-столбец представлен как 2×1 матрица:
Размерность этого вектора:
Используйте linalg::vecdim, или даже вызовите nops(v), чтобы получить длину вектора:
i th компонент этого вектора может быть извлечен двумя способами: или v[i,1] или v[i]:
Мы получаем 2-норму v следующим вызовом:
Опции
Diagonal
|
Создайте диагональную матрицу
С опцией Diagonal диагональные матрицы могут быть созданы с диагональными элементами, взятыми из списка, или вычислили функцией или функциональным выражением.
Dom::DenseMatrix(R)(m, n, List, Diagonal) создает m ×n диагональная матрица, диагональные элементы которой являются записями List.
List должен иметь в большей части min (m, n) записи. Если это имеет меньше элементов, остающиеся диагональные элементы обнуляются.
Записи List преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.
Dom::DenseMatrix(R)(m, n, g, Diagonal) возвращает матрицу, i которой th диагональный элемент является g(i, i), куда индекс i запускается от 1 до min (m, n).
Значения функции преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.
|
Banded
|
Создайте полосную матрицу Теплица
Dom::DenseMatrix(R)(m, n, List, Banded) создает m ×n, соединил матрицу Теплица с элементами List как записи. Количество записей List должно быть нечетным, сказать 2 h + 1 и не должно превышать n. Получившаяся матрица имеет пропускную способность самое большее 2 h + 1.
Матрица Теплица является матрицей, где элементы каждой полосы идентичны. См. также Пример 7.
Все элементы основной диагонали созданной матрицы инициализируются со средним элементом List. Все элементы i th поддиагональ инициализируются с (h + 1 - i) th элемент List. Все элементы i th супердиагональ инициализируются с (h + 1 + i) th элемент List. Все записи на остающемся под - и супердиагонали обнуляются.
Записи List преобразованы в элементы доменного R. Сообщение об ошибке выпущено, если одно из этих преобразований перестало работать.
|
Записи
| issparse | всегда FALSE, когда элементы Dom::DenseMatrix(R) используют плотное представление своих матричных компонентов.
|
| "randomDimen" | установлен в [10,10]. См. метод "random" ниже для деталей. |
Методы
развернуть все
Математические методы
_divide — Разделите матрицы
_divide(A, B)
Сообщение об ошибке выпущено, если размерности A и B не соответствуют.
Этот метод только существует, если R является коммутативным звонком с модулем, т.е. областью категории Cat::Ring.
Этот метод перегружает функциональный _divide для матриц, т.е. можно использовать его в форме A / B, или в функциональном обозначении: _divide(A, B).
_invert — Вычислите инверсию матрицы
_invert(A, Normal =
b)
Если кольцевым R компонента является доменный Dom::Float, приближение с плавающей точкой обратной матрицы вычисляется функциональным numeric::inverse.
Этот метод только существует, если R является областью категории Cat::Ring.
Этот метод перегружает функциональный _invert для матриц, т.е. можно использовать его в форме 1/A или A^(-1), или в функциональном обозначении: _invert(A).
Если Normal = TRUE, то матричная инверсия всегда возвращается в нормированной форме. Для получения дополнительной информации о нормализации, смотрите normal. Если Normal = FALSE, то матричная инверсия может появиться в нормированной форме, но нормализация не гарантируется. Normal = TRUE по умолчанию.
Normal влияет на результаты, только если матрица содержит переменные или точные выражения, такие как sqrt(5) или sin(PI/7).
mod Сопоставьте оператор по модулю с матрицей
_mod(A, n)
n должен быть ненулевым, и a mod n должен быть задан для каждой записи a A.
Этот метод перегружает функциональный mod для матриц; можно использовать его в форме A mod n, или в функциональном обозначении: _mod(A, n).
_mult — Матрицы мультиплие матрицами, векторами и скалярами
_mult(x, y)
_mult(x, y)
Если y имеет доменный тип R или может быть преобразован в такой элемент, соответствующее скалярное умножение вычисляется.
В противном случае y преобразован в матрицу доменного типа x. Если это преобразование перестало работать, то это вызовы метода метод "_mult" области y, дающего все аргументы в том же порядке.
Если x является матрицей того же доменного типа как y, то матричное произведение x y вычисляется. Сообщение об ошибке выпущено, если размерности матриц не соответствуют.
Если x имеет доменный тип R или может быть преобразован в такой элемент, соответствующее скалярное умножение вычисляется.
В противном случае x преобразован в матрицу доменного типа y. Если это преобразование перестало работать, то FAIL возвращен.
Этот метод обрабатывает больше чем два аргумента путем вызова себя рекурсивно с первой половиной всех аргументов и последней половиной всех аргументов. Затем продукт этих двух результатов вычисляется с системной функцией _mult.
Этот метод перегружает функциональный _mult для матриц, т.е. можно использовать его в форме x * y, или в функциональном обозначении: _mult(x, y).
_negate — Инвертируйте матрицу
_negate(A)
Этот метод перегружает функциональный _negate для матриц, т.е. можно использовать его в форме -A, или в функциональном обозначении: _negate(A).
плюс Добавьте матрицы
_plus(A, B, …)
Аргументы A, B , ... преобразованы в матрицы доменного типа Dom::DenseMatrix(R). FAIL возвращен, если одно из этих преобразований перестало работать.
Этот метод перегружает функциональный _plus для матриц, т.е. можно использовать его в форме A + B, или в функциональном обозначении: _plus(A, B).
_power — Целочисленная степень матрицы
_power(A, n)
Если степень, n является отрицательным целым числом затем A, должна быть несингулярной, и R должен быть областью категории Cat::IntegralDomain. В противном случае FAIL возвращен.
Если n является нулем, и кольцевой R компонента является звонком без модуля (т.е. категории Cat::Rng, но не категории Cat::Ring), FAIL возвращен.
Этот метод перегружает функциональный _power для матриц, т.е. можно использовать его в форме A^n, или в функциональном обозначении: _power(A, n).
conjugate — Сопряженное комплексное число матрицы
conjugate(A)
Этот метод только существует, если R реализует метод "conjugate", который вычисляет сопряженное комплексное число элемента доменного R.
Этот метод перегружает функциональный conjugate для матриц, т.е. можно использовать его в форме conjugate(A).
потому что Косинус матрицы
cos(A)
Если A не является квадратным, сообщение об ошибке выпущено. Если область компонента A не позволяет вычисление cos(elem) для произвольного элемента elem звонка компонента, FAIL возвращен.
Этот метод использует функциональный numeric::expMatrix для приближения с плавающей точкой экспоненциала A, если A задан по доменному Dom::Float.
Если некоторые собственные значения A не существуют в R или не могут быть вычислены, то FAIL возвращен.
В символьном случае функции называются exp и linalg::jordanForm. Последний не может смочь вычислить Жорданову форму A. В этом случае возвращен FAIL.
Этот метод только существует, если R является областью категории Cat::Field.
Этот метод перегружает функциональный cos для матриц, т.е. можно использовать его в форме cos(A).
diff Дифференцирование матричных компонентов
diff(A, …)
Этот метод только существует, если R реализует метод "diff".
Этот метод перегружает функциональный diff для матриц, т.е. можно использовать его в форме diff(A, ...). Смотрите Пример 8 и Пример 9.
equal — Тест равенства матриц
equal(A, B)
Обратите внимание на то, что, если R имеет аксиому Ax::systemRep затем, normal используется, чтобы упростить компоненты A и B прежде, чем протестировать их равенство.
exp Экспоненциал матрицы
exp(A, <t>)
Если A не является квадратным, сообщение об ошибке выпущено. Если область компонента A не позволяет вычисление exp(elem) для произвольного элемента elem звонка компонента, FAIL возвращен.
Этот метод использует функциональный numeric::expMatrix для приближения с плавающей точкой экспоненциала A, если A задан по доменному Dom::Float и если t = 1.
Если некоторые собственные значения A не существуют в R или не могут быть вычислены, то FAIL возвращен.
В символьном случае называется функциональный linalg::jordanForm, который не может смочь вычислить Жорданову форму A. В этом случае возвращен FAIL.
Этот метод только существует, если R является областью категории Cat::Field.
Этот метод перегружает функциональный exp для матриц, т.е. можно использовать его в форме exp(A, ...).
расширение Расширьте матричные компоненты
expand(A)
Этот метод только существует, если R реализует метод "expand", или если R имеет аксиому Ax::systemRep (в этом случае, системная функция, expand используется).
Этот метод перегружает функциональный expand для матриц, т.е. можно использовать его в форме expand(A).
фактор Факторизация диагональной матрицы
factor(A)
Факторный s является GCD всех компонентов матричного A. Следовательно, этот метод только существует, если R имеет категорию Cat::GcdDomain.
Этот метод перегружает функциональный factor для матриц, т.е. можно использовать его в форме factor(A).
float — Приближение с плавающей точкой матричных компонентов
float(A)
Этот метод только существует, если R реализует метод "float".
Примечание
Обычно приближения с плавающей точкой не являются элементами R! Например, Dom::Integer реализует такой метод, но приближение с плавающей точкой целого числа не может быть повторно преобразовано в целое число.
Этот метод проверяет, может ли получившаяся матрица быть преобразована в доменный тип A, только если testargs возвращает TRUE (например, если вы вызываете этот метод от интерактивного уровня MuPAD).
В противном случае нужно заботиться, что возвращенная матрица совместима со своим звонком компонента.
gaussElim — Исключение Гаусса
gaussElim(A)
Если матрица не является квадратной, т.е. детерминант A не задан, то третья запись возвращенного списка является значением FAIL.
Этот метод только существует, если кольцевой R компонента является интегральной областью, т.е. областью категории Cat::IntegralDomain.
Если R имеет метод "pivotSize", то элемент центра самого маленького размера выбран на каждом вертящемся шаге, посредством чего pivotSize должен возвратить положительное целое число, представляющее “размер” элемента.
Если никакой такой метод не задан, Исключение Гаусса без стратегии центра применяется к A.
Если R имеет аксиому Ax::efficientOperation ("_invert") и является категории Cat::Field, то обычное Исключение Гаусса используется. В противном случае устранение без частей выполняется на A.
Если R реализует метод "normal", это используется, чтобы упростить последующие вычисления процесса Исключения Гаусса.
Обратите внимание на то, что, если R не реализует метод, "normal", но элементы R представлен областями ядра, т.е. R имеет аксиому Ax::systemRep, системная функция, normal используется вместо этого.
identity — Единичная матрица
identity(n)
Этот метод только существует, если кольцевой R компонента имеет категорию Cat::Ring, т.е. звонок с модулем.
int — Интегрирование матричных компонентов
int(A, …)
Этот метод только существует, если R реализует метод "int".
Этот метод перегружает системную функцию int для матриц, т.е. можно использовать его в форме int(A, ...).
iszero — Протестируйте на нулевые матрицы
iszero(A)
Обратите внимание на то, что там может существовать больше чем одно представление нулевой матрицы данной размерности, если R не имеет Ax::canonicalRep.
Если R реализует метод "normal", это используется, чтобы упростить компоненты A для нулевого теста.
Обратите внимание на то, что, если R не реализует такой метод, но элементы R представлены областями ядра, т.е. R имеет аксиому Ax::systemRep, системная функция, normal используется вместо этого.
Этот метод перегружает функциональный iszero для матриц, т.е. можно использовать его в форме iszero(A).
matdim — Матричная размерность
норма Норма матриц и векторов
norm(A, Infinity)
norm(A, Maximum)
norm(v, Infinity)
norm(v, Maximum)
norm(A, Frobenius)
norm(A, 1)
norm(v, Euclidean)
norm(v, k)
norm(A, Maximum) вычисляет максимальную норму матричного A, который является максимальной суммой строки (сумма строки является суммой норм каждого компонента подряд).
Если доменный R не реализует методы "max" и "norm", FAIL возвращен.
Используя norm(v, Infinity) для векторного v возвращена максимальная норма всех элементов.
Если доменный R не реализует методы "max" и "norm", FAIL возвращен.
Используя norm(v, Maximum) для векторного v возвращена максимальная норма всех элементов.
Если доменный R не реализует методы "max" и "norm", FAIL возвращен.
norm(A, Frobenius) вычисляет норму Фробениуса A, который является квадратным корнем из суммы квадратов норм каждого компонента.
Если результатом больше не является элемент доменного R, или если R не реализует метод "norm", FAIL возвращен.
norm(A, 1) вычисляет 1 норму матричного A, который является максимальной суммой норм элементов каждого столбца. Если R не реализует методы "max" и "norm", FAIL возвращен.
norm(v, Euclidean) вычисляет Евклидову норму (2-норма) векторного v, который задан, чтобы быть квадратным корнем из суммы норм элементов v, повышенного до квадрата.
FAIL возвращен, если результатом больше не является элемент доменного R. Функциональный linalg::scalarProduct используется, чтобы вычислить Евклидову норму векторного v.
Если R не реализует метод "norm", FAIL возвращен.
norm(v, k) вычисляет k - норма векторного v, который задан, чтобы быть k th корень суммы норм элементов v, повышенного до k th степень.
FAIL возвращен, если результатом больше не является элемент доменного R. Для k = 2, функциональный linalg::scalarProduct используется, чтобы вычислить 2-норму v.
Если R не реализует метод "norm", FAIL возвращен.
Метод norm перегружает функциональный norm для матриц, т.е. можно использовать его в форме norm(A k ), где k является или Infinity, Frobenius или положительное целое число. Значением по умолчанию k является Infinity.
normal — Упрощение матричных компонентов
normal(A)
Если R не реализует метод, "normal", но элементы R представлен областями ядра, т.е. R имеет аксиому Ax::systemRep, то системная функция normal применяется к компонентам A. В противном случае normal(A) возвращает A без любых изменений.
Этот метод перегружает функциональный normal для матриц, т.е. можно использовать его в форме normal(A).
ненули Количество ненулевых компонентов матрицы
nonZeroes — Количество ненулевых компонентов матрицы
nonZeroOperands — Возвратите последовательность всех ненулевых операндов
nonZeroOperands(A)
Этот метод полезен для получения информации о ненулевых записях. Например, чтобы узнать типы записей в матрице, не нужно считать все операнды op(A), потому что это также включило бы нулевые записи. Для больших матриц с немногими записями намного более эффективно использовать этот метод, чтобы извлечь записи.
random — Случайная генерация матрицы
random()
Этот метод только существует, если R реализует метод "random".
Размерность матрицы также выбрана случайным образом, но это ограничивается значениями, данными в "randomDimen" (см. “Записи” выше).
Чтобы изменить значение записи "randomDimen" для доменного MatR, созданного с Dom::DenseMatrix, нужно сначала оставить без защиты доменный Dom (см. unprotect для деталей).
sin — Синус матрицы
sin(A)
Если A не является квадратным, сообщение об ошибке выпущено. Если область компонента A не позволяет вычисление sin(elem) для произвольного элемента elem звонка компонента, FAIL возвращен.
Этот метод использует функциональный numeric::expMatrix для приближения с плавающей точкой экспоненциала A, если A задан по доменному Dom::Float.
Если некоторые собственные значения A не существуют в R или не могут быть вычислены, то FAIL возвращен.
В символьном случае функции называются exp и linalg::jordanForm. Последний не может смочь вычислить Жорданову форму A. В этом случае возвращен FAIL.
Этот метод только существует, если R является областью категории Cat::Field.
Этот метод перегружает функциональный sin для матриц, т.е. можно использовать его в форме sin(A).
sqrt Квадратный корень из матрицы
sqrt(A, <sqrtfunc>)
Возвращенный матричный B с B 2 = A, таким образом, что собственные значения B являются квадратными корнями из собственных значений A или FAIL, если квадратный корень из матрицы не существует. Для вычисления квадратных корней из собственных значений функция, удовлетворяющая sqrtfunc (a) 2 = a для каждого элемента, a содействующего звонка A может быть дан как дополнительный второй аргумент.
Для получения дополнительной информации мы обращаемся к странице справки функционального linalg::sqrtMatrix.
testeq — Тестирование на равенство двух матриц
tr — Трассировка квадратной матрицы
tr(A)
Если A не является квадратным, то сообщение об ошибке выпущено.
перемещение Транспонируйте матрицы
Методы доступа
_concat — Горизонтальная конкатенация матриц
_concat(A, B, …)
Сообщение об ошибке выпущено, если данные матрицы не имеют одинакового числа строк.
Этот метод перегружает функциональный _concat для матриц, т.е. можно использовать его в форме A . B . ..., или в функциональном обозначении: _concat(A, B, ...).
_index — Индексирование матриц
_index(A, i, j)
_index(A, r1 .. r2, c1
.. c2)
_index(v, i)
_index(v, i1 .. i2)
Если i и j не являются целыми числами, то вызов этого метода возвращается в его символьной форме (типа "_index") с оцененными аргументами.
В противном случае сообщение об ошибке дано, если i и j не являются допустимыми индексами строки и столбца, соответственно.
Примечание
Обратите внимание на то, что этот метод использует системную функцию context, чтобы оценить запись в контексте среды вызова.
_index(A,r1..r2,c1..c2) возвращает субматрицу A, созданного строками A с индексами от r1 до r2 и столбцов A с индексами от c1 до c2.
_index(v,i) возвращает i th запись векторного v.
Сообщение об ошибке выпущено, если v не является вектором.
Если i не является целым числом, то вызов этого метода возвращается в его символьной форме (типа "_index") с оцененными аргументами.
В противном случае сообщение об ошибке дано, если i - меньше чем один или больше, чем размерность v.
Примечание
Обратите внимание на то, что этот метод использует системную функцию context, чтобы оценить запись в контексте среды вызова.
_index(v,i1..i2) возвращает подвектор v, сформированного записями с индексом i1 к i2. См. также метод "op".
Сообщение об ошибке выпущено, если v не является вектором.
Этот метод перегружает функциональный _index для матриц, т.е. можно использовать его в форме A[i, j], A[r1..r2, c1..c2], v[i] и v[i1..i2], соответственно, или в функциональном обозначении: _index(A, ...).
concatMatrix — Горизонтальная конкатенация матриц
col — Извлечение столбца
col(A, c)
Сообщение об ошибке выпущено, если c - меньше чем один или больше, чем количество столбцов A.
delCol — Удаление столбца
delCol(A, c)
NIL возвращен, если A состоит только из одного столбца.
Сообщение об ошибке выпущено, если c - меньше чем один или больше, чем количество столбцов A.
delRow — Удаление строки
delRow(A, r)
NIL возвращен, если A состоит только из одной строки.
Сообщение об ошибке выпущено, если r - меньше чем один или больше, чем количество строк A.
evalp — Оценка матриц полиномов в определенный момент
evalp(A, x = a, …)
Этот метод только задан, если R является полиномиальным звонком категории Cat::Polynomial.
Этот метод перегружает функциональный evalp для матриц, т.е. можно использовать его в форме evalp(A, x = a).
длина Длина матрицы
length(A)
Этот метод перегружает функциональный length для матриц, т.е. можно использовать его в форме length(A).
map — Примените функцию к матричным компонентам
map(A, func,
<expr, …>)
Примечание
Обратите внимание на то, что значения функции преобразованы в элементы доменного R, только если testargs возвращает TRUE (например, если вы вызываете этот метод от интерактивного уровня MuPAD).
Если testargs возвратит FALSE, то нужно гарантировать, что вызовы функции возвращают элементы доменного типа R, в противном случае получившаяся матрица, которая имеет доменный тип Dom::DenseMatrix(R), имела бы компоненты, которые не являются элементами доменного R!
Этот метод перегружает функциональный map для матриц, т.е. можно использовать его в форме map(A, func, ...).
mapNonZeroes — Примените функцию к ненулевым компонентам матрицы
mapNonZeroes(A, f,
<p1, p2, …>)
nops — Количество компонентов матрицы
nops(A)
Этот метод перегружает функциональный nops для матриц, т.е. можно использовать его в форме nops(A).
op Компонент матрицы
op(A, i)
op(A)
Этот метод возвращает последовательность выражения всех компонентов A.
См. также метод "_index".
Этот метод перегружает функциональный op для матриц, т.е. можно использовать его в форме op(A, i) и op(A), соответственно.
row — Извлечение строки
row(A, r)
Сообщение об ошибке выпущено, если r - меньше чем один или больше, чем количество строк A.
setCol — Заменяя столбец
setCol(A, c, v)
Сообщение об ошибке выпущено, если c - меньше чем один или больше, чем количество строк A.
setRow — Заменяя строку
setRow(A, r, v)
Сообщение об ошибке выпущено, если r - меньше чем один или больше, чем количество строк A.
stackMatrix — Вертикальная конкатенация матриц
stackMatrix(A, B, …)
Сообщение об ошибке выпущено, если данные матрицы не имеют одинакового числа столбцов.
subs — Замена матричных компонентов
subs(A, …)
Примечание
Обратите внимание на то, что значения функции преобразованы в элементы доменного R, только если testargs возвращает TRUE (например, если вы вызываете этот метод от интерактивного уровня MuPAD).
Если testargs возвратит FALSE, то нужно гарантировать, что вызовы функции возвращают элементы доменного типа R, в противном случае получившаяся матрица, которая имеет доменный тип Dom::DenseMatrix(R), имела бы компоненты, которые не являются элементами доменного R!
Этот метод перегружает функциональный subs для матриц, т.е. можно использовать его в форме subs(A, ...).
subsex — Расширенная замена матричных компонентов
subsex(A, …)
Примечание
Обратите внимание на то, что результаты замен преобразованы в элементы доменного R, только если testargs возвращает TRUE (например, если вы вызываете этот метод от интерактивного уровня MuPAD).
Если testargs возвратит FALSE, то нужно гарантировать, что результаты замен имеют доменный тип R, в противном случае получившаяся матрица, которая имеет доменный тип Dom::DenseMatrix(R), имела бы компоненты, которые не являются элементами доменного R!
Этот метод перегружает функциональный subsex для матриц, т.е. можно использовать его в форме subsex(A, ...).
subsop — Замена операнда матричных компонентов
subsop(A, i = x, …)
Примечание
Обратите внимание на то, что x преобразован в доменный R, только если testargs возвращает TRUE (например, если вы вызываете этот метод от интерактивного уровня MuPAD).
Если testargs возвращает FALSE, то x должен быть элементом R, в противном случае получившаяся матрица, которая имеет доменный тип Dom::DenseMatrix(R), имела бы компоненты, которые не являются элементами доменного R!
См. также метод "set_index".
Этот метод перегружает функциональный subsop для матриц, т.е. можно использовать его в форме subsop(A, ...).
swapCol — Свопинг столбцов матрицы
swapCol(A, c1, c2)
swapCol(A, c1, c2, r1
.. r2)
Сообщение об ошибке выпущено, если один из индексов столбца - меньше чем один или больше, чем количество столбцов A.
swapCol(A,c1,c2,r1..r2) подкачивает столбец с индексом c1 и столбец с индексом c2 A, но путем взятия только тех компонентов столбца, которые лежат в строках с индексами r1 к r2.
Сообщение об ошибке выпущено, если один из индексов столбца - меньше чем один или больше, чем количество столбцов A, или если один из индексов строки - меньше чем один или больше, чем количество строк A.
swapRow — Свопинг строк матрицы
swapRow(A, r1, r2)
swapRow(A, r1, r2, c1
.. c2)
Сообщение об ошибке выпущено, если один из индексов строки - меньше чем один или больше, чем количество строк A.
swapCol(A,r1,r2,c1..c2) подкачивает строку с индексом r1 и строка с индексом r2 A, но путем взятия только тех компонентов строки, которые лежат в столбцах с индексами c1 к c2.
Сообщение об ошибке выпущено, если один из индексов строки - меньше чем один или больше, чем количество строк A, или если один из индексов столбца - меньше чем один или больше, чем количество столбцов A.
set_index — Установка матричных компонентов
set_index(A, i, j, x)
set_index(v, i, x)
Примечание
Обратите внимание на то, что x преобразован в элемент доменного R, только если testargs возвращает TRUE, и i и j являются целыми числами (например, если вы вызываете этот метод от интерактивного уровня MuPAD). Если x является матрицей того же типа как A или может быть преобразован в матрицу того же типа как A и индексы, i или j являются областями значений, соответствующими субматрице A, то x заменяет соответствующую субматрицу в A.
В противном случае нужно заботиться, что x имеет доменный тип R.
См. также метод "subsop".
set_index(v,i,x) заменяет i th запись векторного v x.
set_index на векторах перегружает функциональный set_index для матриц, т.е. можно использовать его в форме A[i, j] := x и v[i] := x, соответственно, или в функциональном обозначении: A := set_index(A, i, j, x) или v := set_index(v, i, x).
zip Объедините матрицы покомпонентно
zip(A, B, func,
<expr, …>)
Номер строки возвращенной матрицы является минимумом номеров строк A и B, и его номер столбца является минимумом номеров столбцов A и B.
Примечание
Обратите внимание на то, что значения функции преобразованы в элементы доменного R, только если testargs возвращает TRUE (например, если вы вызываете этот метод от интерактивного уровня MuPAD).
Если testargs возвратит FALSE, то нужно гарантировать, что вызовы функции возвращают элементы доменного типа R, в противном случае получившаяся матрица, которая имеет доменный тип Dom::DenseMatrix(R), имела бы компоненты, которые не являются элементами доменного R!
Этот метод перегружает функциональный zip для матриц, т.е. можно использовать его в форме zip(A, B, ...).
Методы преобразования
\convert Преобразование в матрицу
convert(x)
FAIL возвращен, если преобразование перестало работать.
x может или быть массивом, матрицей или списком (подсписков, смотрите параметр ListOfRows в “Создании Элементов” выше). Их записи должны затем быть конвертируемы в элементы доменного R.
convert_to — Матричное преобразование
convert_to(A, T)
T может или быть DOM_ARRAY, DOM_LIST или область, созданная Dom::DenseMatrix или Dom::SquareMatrix. Элементы A должны быть конвертируемы в элементы доменного R.
Используйте функциональный expr, чтобы преобразовать A в объект области ядра (см. ниже).
create — Определение матриц без преобразований компонента
create(x, …)
Этот метод работает более эффективный, чем если бы вы создаете матрицы путем вызова метода "new" области, потому что это избегает любого преобразования компонентов. Нужно гарантировать, что компоненты имеют правильный доменный тип, в противном случае ошибки времени выполнения могут быть вызваны.
Если x является списком подсписков, это может быть хорошая идея сначала, чтобы создать двумерный массив из того списка прежде, чем вызвать этот метод. Это - то, вследствие того, что создание матрицы от массива является самым быстрым способом, которым можно достигнуть.
Обратите внимание на то, что при создании двумерного массива из списка подсписков, подсписки должны иметь то же число элементов.
expr) Матричное преобразование в объект области ядра
expr(A)
Результатом является массив, представляющий матричный A, где каждая запись является объектом области ядра.
Этот метод перегружает функциональный expr для матриц, т.е. можно использовать его в форме expr(A).
expr2text — Матричное преобразование в строку
expr2text(A)
Этот метод перегружает функциональный expr2text для матриц, т.е. можно использовать его в форме expr2text(A).
Технические методы
assignElements — Несколько присвоение на матрицы
assignElements(A, …)
Присвоенные компоненты должны иметь доменный тип R, неявное преобразование компонентов в элементы доменного типа, R не выполняется.
Этот метод перегружает функциональный assignElements для матриц, т.е. можно использовать его в форме assignElements(A, ...).
mkDense — Преобразование матрицы к массиву
mkDense(Array)
mkDense(List)
mkDense(r, c, List)
mkDense(List) пытается преобразовать список List в массив a. Результатом является или FAIL, если это не возможно, или список [r, c, a], где положительные целые числа r и c дают размерность a. Смотрите параметры List и ListOfRows в “Создании Элементов” выше для допустимых форматов List.
a массивов имеет тот размерности, если r или c равны одному. Записи a были преобразованы в элементы доменного R.
mkDense(r,c,List) пытается преобразовать список List в массив a размерности времена r c.
Результатом является или FAIL, если это не возможно, или список [r, c, a].
a массивов имеет тот размерности, если r или c равны одному. Записи a были преобразованы в элементы доменного R.
печать Печать матриц
print(A)
Примечание
Обратите внимание на то, что в целом не полезно распечатать очень большие матрицы. Следовательно, предупреждающее сообщение быть отображенным, если размер матрицы переступает через определенную размерность – печать таких матриц может быть сделана при помощи функционального "doprint".
doprint — Печать очень больших матриц
unapply — Создайте процедуру из матрицы
unapply(A, <x, …>)
Этот метод перегружает функциональный fp::unapply для матриц, т.е. можно использовать его в форме fp::unapply(A).
Смотрите также
Области MuPAD
![]()
![]()
![]()

![]() :
:
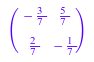
![]()
![]()
![]()
![]()
![]()

![]()

![]()
![]()

![]()



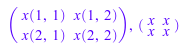

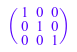

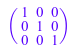

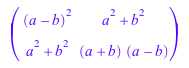

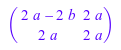
![]()
![]()

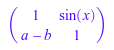

![]()
![]()
![]()
![]()
![]()
![]()