график::конформный график функций (с комплексным знаком)
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
plot::Conformal(f, z = z1 .. z2, <a = amin .. amax>, options)
plot::Conformal(f(z), z = z_1..z_2 ) является графиком конформного функционального f на комплексном интервале z_1..z_2.
plot::Conformal создает графики (конформных) комплексных функций одной комплексной переменной. Они отображены путем показа изображения прямоугольной сетки на интервале.
По умолчанию атрибут LineColorType = Flat установлен. Все кривые отображены с цветом, данным атрибутом LineColor (или Color, если коротко).
При определении атрибута LineColorType = Dichromatic цветное смешение от LineColor до LineColor2 используется (“высота, окрашивающая”).
При определении атрибута LineColorType = Functional, не задавая LineColorFunction, все кривые, параметризованные действительной частью точек предызображений, отображен с чистым цветом LineColor, тогда как все кривые, параметризованные мнимой частью точек предызображений, отображены с чистым цветом LineColor2.
Определяемый пользователем LineColorFunction является процедурой (z, x, y, flag) -> RGB-color, который будет вызван комплексными аргументами z с плавающей точкой из области значений предварительных изображений конформного функционального f, действительные значения с плавающей точкой x = Re(f(z)), y = Im(f(z)) и целочисленное значение flag, который имеет значения 1 или 2. Флаговое значение 1 определяет цвет кривых, параметризованных действительной частью z, флаговое значение 2 определяет цвет кривых, параметризованных мнимой частью z. Функция управления цветом должна возвратить цвет RGB, т.е. список 3 действительных значений с плавающей точкой между 0,0 и 1.0. Например,
LineColorFunction = proc(z, x, y, flag)
begin
if flag = 1 then
return(RGB::Blue)
else
return(RGB::Red)
end_if;
end_proc Re(z) синего цвета, в то время как ортогональные кривые, параметризованные Im(z), отображены в красном.Смотрите примеры в документации RGB для другого способа отобразить комплексные функции.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AdaptiveMesh | адаптивная выборка | 0 |
AffectViewingBox | влияние объектов на ViewingBox сцены | TRUE |
AntiAliased | сглаженные строки и точки? | TRUE |
Color | основной цвет | RGB::Blue |
Frames | количество кадров в анимации | 50 |
Function | выражение function или процедура | |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | TRUE |
LineColor | цвет строк | RGB::Blue |
LineWidth | ширина строк | 0.35 |
LineColor2 | цвет строк | RGB::DeepPink |
LineStyle | тело, подчеркнутые штриховой линией или пунктирные линии? | Solid |
LinesVisible | видимость строк | TRUE |
LineColorType | типы окраски строки | Flat |
LineColorFunction | функциональная окраска строки | |
LineColorDirection | направление цветовых переходов на строках | [0, 1] |
LineColorDirectionX | x-компонент направления цветовых переходов на строках | 0 |
LineColorDirectionY | y-компонент направления цветовых переходов на строках | 1 |
Mesh | количество точек выборки | [11, 11] |
Name | имя объекта графика (для браузера и легенды) | |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
PointSize | размер точек | 1.5 |
PointsVisible | видимость точек mesh | FALSE |
Submesh | плотность подmesh (дополнительные точки выборки) | [0, 0] |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 .. 10.0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11] |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
XMesh | количество точек выборки для параметра “x” | 11 |
XSubmesh | плотность дополнительных точек выборки для параметра “x” | 0 |
YMesh | количество точек выборки для параметра “y” | 11 |
YSubmesh | плотность дополнительных точек выборки для параметра “y” | 0 |
ZMax | окончательное значение параметра “z” | |
ZMin | начальное значение параметра “z” | |
ZName | имя параметра “z” | |
ZRange | область значений параметра “z” |
Путем графического вывода тождественного отображения мы представлены предварительное изображение, используемое plot::Conformal:
plot(plot::Conformal(z, z = 0..1+I))
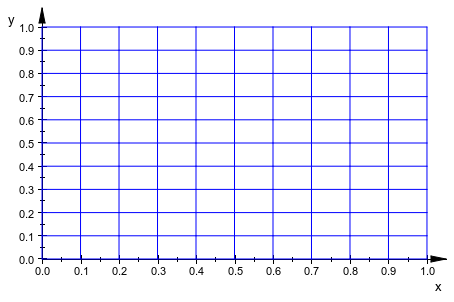
Важное свойство конформных функций, насколько графики затронуты, то, что ортогональные строки сопоставлены на кривые, встречающиеся ортогонально:
plot(plot::Conformal(z^2, z = 0..1+I))
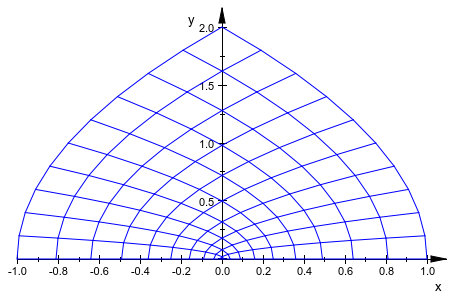
Это свойство позволяет визуально обнаруживать перекрывающиеся области (в некоторых случаях); в следующем примере дело обстоит так в левой полуплоскости:
plot(plot::Conformal(z^(3/2), z = -1-I..1+I))
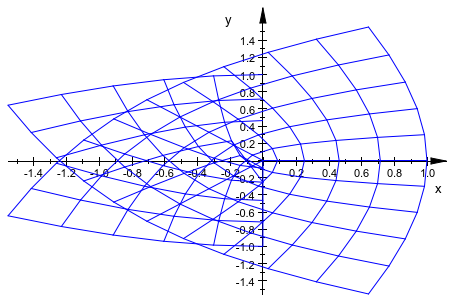
Mesh по умолчанию может в некоторых случаях быть слишком крупной:
plot(plot::Conformal(sin(z^2), z = 0..1+I))

Существует по крайней мере три способа улучшить этот график. Во-первых, мы можем установить Mesh на более высокое значение:
plot(plot::Conformal(sin(z^2), z = 0..1+I, Mesh = [50, 50]))
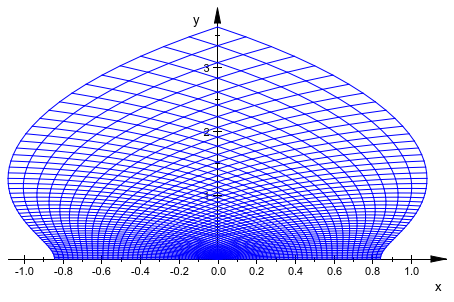
Другая опция должна была бы увеличить Submesh, чтобы стать более сглаженной, не больше, строки:
plot(plot::Conformal(sin(z^2), z = 0..1+I, Submesh = [2, 2]))
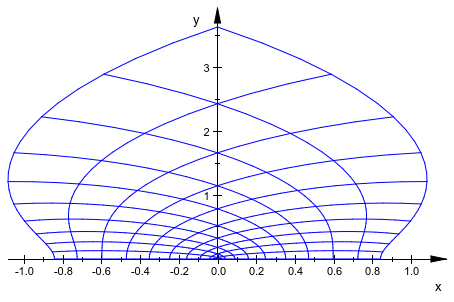
Наконец, мы можем также попросить адаптивное улучшение подmesh установкой AdaptiveMesh к некоторому положительному значению:
plot(plot::Conformal(sin(z^2), z = 0..1+I, AdaptiveMesh = 2))
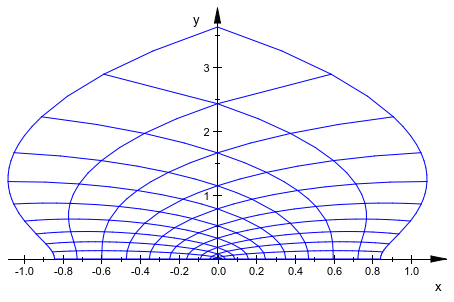
Вот является изображение комплексного прямоугольника 0 ≤ Re (z) ≤ x, 0 ≤ ℑ (z) ≤ 1 в соответствии с картой z → besselJ(0, z). Мы выбираем x в качестве второго положительного корня Im(besselJ(0, x + I)):
numeric::solve(Im(besselJ(0, x + I)), x = i .. i+1) $ i = 0..7
![]()
plot(plot::Conformal(besselJ(0, z), z = 0 .. 6.9934 + I,
Mesh = [31, 10]))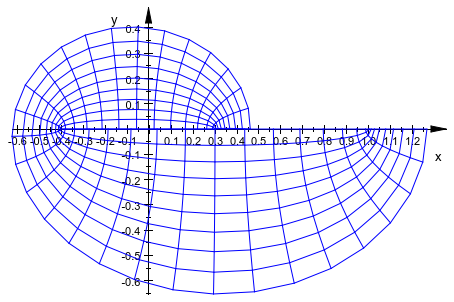
|
Выражение в
|
|
Независимая переменная: идентификатор или индексированный идентификатор.
|
|
(Комплекс) передвигаются, по которому должен быть построен
|
|
Параметр анимации, заданный как |