LineColorFunction, FillColorFunction
Функциональная окраска строки
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Сводные данные значения
FillColorFunction, LineColorFunction | Дополнительный | Функция управления цветом (см. ниже), |
Графические примитивы
Описание
Эти опции принимают функции, которые задают цвет графика в произвольных точках.
Используя FillColorType и LineColorType, пользователь может управлять цветом многих графических объектов. Установкой, обеспечивающей самое подробное (и самый сложный) управление, является Functional. В этом случае функция управления цветом должна быть обеспечена с помощью одного из LineColorFunction, FillColorFunction.
Функция управления цветом может быть списком трех или четырех выражений.
Если три выражения даны, они задают цвета RGB. Если четыре выражения даны, они задают цвета RGBA. Дополнительную информацию см. во введении на спецификациях цветов.
Выражения могут содержать идентификаторы, связанные в соответствующем объекте. Например, в plot::Function2d(sin(x), x=0..PI), функция управления цветом может относиться к x. Более официально выражения могут содержать идентификаторы, найденные в атрибутах XName, YName, ZName, UName, VName, и ParameterName графика возражает, что они найдены в.
Все эти выражения, для значений в данных областях значений, должны оценить к вещественным числам в области значений
. Действительные значения вне этой области значений не приводят к ошибкам, они просто отсекаются.
См. также Пример 1.
Также функция управления цветом может быть процедурой или функциональной средой.
Процедура (или функциональная среда) используемый в качестве функции управления цветом должна возвратить списки трех или четырех вещественных чисел в области значений
. Действительные значения вне этой области значений отсекаются. (Если эта функция когда-нибудь возвращает список четырех чисел, она должна всегда делать так.) Список трех чисел интерпретирован как цвет RGB, в то время как список четырех значений интерпретирован как цвет RGBA. Дополнительную информацию см. во введении на спецификациях цветов.
Номер и значение аргументов, с которыми вызвана функция управления цветом, зависят от типа объекта. Неофициально, мы имеем:
| Введите (сокращенный) | Параметры |
|---|---|
Conformal(f(z)) | z, Re(f(z)), Im(f(z)), flag (с flag = 1 или flag = 2) |
Curve2d(x(u),y(u)) | u, x(u), y(u) |
Curve3d(x(u),y(u),z(u)) | u, x(u), y(u), z(u) |
Cylindrical(r(u,v),phi(u,v),z(u,v)) | u, v, r(u,v), phi(u,v), z(u,v), x(u), y(u), z(u) |
Density(f(x,y)) | x, y, f(x,y) |
plot::Dodecahedron | Смотрите ниже. |
Function2d(f(x)) | x, f(x) |
Function3d(f(x,y)) | x, y, f(x,y) |
plot::Hexahedron | Смотрите ниже. |
Icosahedron | Смотрите ниже. |
Implicit2d(f(x,y), Contours=[c]) | x, y, D([1],f)(x,y), D([2],f)(x,y), c |
Implicit3d(f(x,y,z), Contours=[c]) | x, y, z, D([1],f)(x,y,z), D([2],f)(x,y,z), D([3],f)(x,y,z), c |
Matrixplot | x, y, z |
Octahedron | Смотрите ниже. |
Polar([r(t),phi(t)]) | t, r(t), phi(t), x(t), y(t) |
Polygon2d([..,[xi,yi],..]) | xi, yi, i |
| xi, yi, zi, i |
| u, Re(z), Im(z) |
Spherical(r(u,v),phi(u,v),thet(u,v)) | u, v, r(u,v), phi(u,v), thet(u,v), x, y, z |
Streamlines2d(v(x,y), w(x, y)) | x, y, v(x,y), w(x,y), t, l, n |
Surface(x(u,v),y(u,v),z(u,v)) | u, v, x(u,v), y(u,v), z(u,v) |
SurfaceSTL | Смотрите ниже. |
SurfaceSet | Смотрите ниже. |
Tetrahedron | Смотрите ниже. |
Tube | Смотрите ниже. |
VectorField2d(v(x,y),w(x,y)) | x, y, v(x,y), w(x,y) |
XRotate(f(x)) | x, phi, x, y(x,phi), z(x,phi) |
ZRotate(f(t)) | t, phi, x(t,phi), y(t,phi), f(t) (=z(t,phi)) |
Кроме того, для анимированных объектов, текущее значение параметра анимации обеспечивается.
Dodecahedron, Hexahedron, Icosahedron, SurfaceSTL, SurfaceSet и Tetrahedron создаются из треугольников; функции управления цветом вызваны однажды для каждой вершины этих треугольников и передаются количество треугольника (целочисленное количество, запускающееся в 1), координаты вершины и параметра анимации, если это используется.
Для plot::Tube функциям управления цветом дают координаты в настоящее время посещаемой точки на центральной кривой, сопровождаемой координатами точки на поверхности, сопровождаемой параметром анимации, если таковые имеются. (Который приводит семь аргументов в целом.)
Примеры ниже показа различные среды использования функций управления цветом для некоторых типов объектов упоминаются выше.
Примеры
Пример 1
По умолчанию большинство 3D объектов в MuPAD® получает “высоту, окрашивающую”:
plot(plot::Function3d(sin(x)*y^3))
Чтобы изменить направление этого цвета, можно использовать FillColorFunction:
xmin := -5:
xmax := 5:
color := zip(RGB::Red, RGB::CornflowerBlue,
(a, b) -> (x-xmin)/(xmax-xmin)*a
+(xmax-x)/(xmax-xmin)*b)
plot(plot::Function3d(sin(x)*y^3,
FillColorFunction = color))
Пример 2
Анимированные функции управления цветом могут быть объединены со статическими объектами:
plot(
plot::Curve2d([sin(3*x), sin(4*x + 1)], x = 0..2*PI,
LineColorFunction = ((u, x, y, a) ->
[(u-a)/5, (u-a)/5, 1]),
a = -5..6)
)
cf := (i, x, y, z, a) -> [RGB::Red,
RGB::Green,
RGB::Blue][(floor(a*i)
mod 3) + 1]:
plot(plot::Icosahedron(FillColorFunction = cf,
a = 0..9))
Пример 3
Функция управления цветом должна сгенерировать значения в цветовом пространстве RGB. Поскольку plot::Box не позволяет FillColorFunction, мы используем шесть (тривиальных) объектов Surface показать за пределами этого цветового пространства:
rgb := (u, v, x, y, z) -> [x, y, z]:
plot(plot::Surface(formula, u = 0..1, v = 0..1,
FillColorFunction = rgb)
$ formula in [[0, u, v], [1, u, v],
[u, 0, v], [u, 1, v],
[u, v, 0], [u, v, 1]],
plot::Box(0..1, 0..1, 0..1, Filled = FALSE,
LineColor = RGB::Black.[0.25]),
Scaling = Constrained, Axes = None,
ULinesVisible = FALSE, VLinesVisible = FALSE,
Lighting = None, CameraDirection = [4, 7, 3])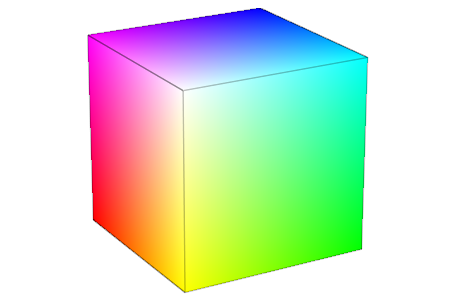
Цвета RGB являются очень техническим способом задать цвет. Цветовое пространство HSV более популярно у разработчиков, поскольку там “оттенок” (т.е. воспринятый тип цвета) не является комбинацией трех чисел, а скорее одним из чисел, составляющих цвет:
hsv := (u, v, r, phi, z) -> RGB::fromHSV([180/PI*phi, r, z]):
plot(plot::Cylindrical([z, phi, z], z = 0..1, phi = 0..2*PI,
FillColorFunction = hsv),
plot::Cylindrical([r, phi, 1], r = 0..1, phi = 0..2*PI,
FillColorFunction = hsv),
plot::Circle3d(1, [0, 0, 1], [0, 0, 1],
Color = RGB::Black.[0.25]),
ZXRatio = 1.5, Scaling = Unconstrained,
Axes = None, Lighting = None,
ULinesVisible = FALSE, VLinesVisible = FALSE,
CameraDirection = [-17, -12, 3])
Пример 4
Цветовое пространство HSV особенно подходит для быстрой окраски цилиндрический,полярный, или сферических графиков, из-за его кругового характера:
hsv := (u, v, r, phi,thet) ->
RGB::fromHSV([180/PI*(phi+(thet+2)^3/PI^2),
3/4+sin(u)/4, 1]):
plot(plot::Spherical([1, u, v], u = 0..2*PI, v = 0..PI,
FillColorFunction = hsv))
Существуют другие примеры, где циклическая природа пригождается, также:
hsv := (x, y, z) -> RGB::fromHSV([150*z, 1, 1]):
plot(plot::Function3d(sin(x*y)*(x-y), x = -3..3, y = -3..3,
Submesh = [2, 2], FillColorFunction = hsv))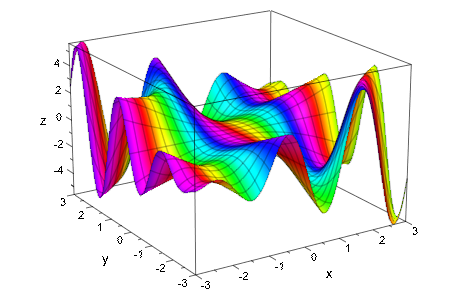
Следующий пример занимает много времени, чтобы вычислить. Сокращение набора значений для Mesh приводит к более короткому вычислению, в то время как более высокие значения приводят к изображению с более прекрасными деталями:
c := 0.377+0.2*I:
julia := proc(x, y)
local i, z;
begin
i := 0;
z := float(x + I*y);
while i < 1000 and abs(z) < 4 do
z := z^2 + c;
i := i + 1;
end_while;
i;
end_proc:
Jcol := (x, y, i) -> if i >= 1000 then
RGB::Black
else
RGB::fromHSV([i, 1, 3/4+i/2000])
end:
plot(plot::Density(julia, x = 0..0.5, y=0.25..0.75,
FillColorFunction = Jcol,
Mesh = [100,75]))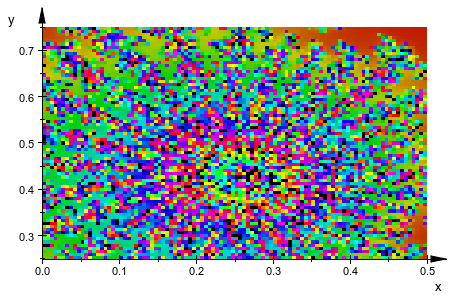
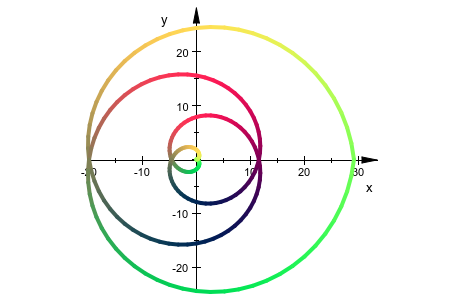
Пример 5
Другой способ получить сглаженный цветовой переход состоит в том, чтобы использовать промежуточную периодическую функцию, например, тригонометрические единицы (отметьте (1+sin(a))/2: нам нужны значения между 0 и 1):
plot(
plot::Polar([r*surd(r, 3), r], r = -4*PI..4*PI,
AdaptiveMesh = 2,
LineColorFunction = [(sin(r) + 1)/2,
(cos(r/2) + 1)/2,
1/3],
LineWidth = 1*unit::mm)
)
Это также запрашивает циклические цвета с точки зрения времени:
plot(plot::Function3d(sin(x)+sin(y), x = -5..5, y = -5..5,
FillColorFunction = [(x+5)/10, (y+5)/10,
abs(x+y+5*cos(a))/15,
(1+cos(x+y^2-a))/2],
a = 0..2*PI),
CameraDirection = [-1, -3, 3],
Scaling = Constrained)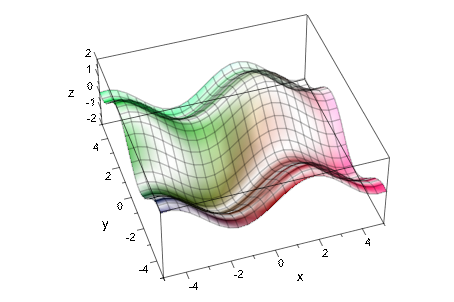
Алгоритмы
Анимация обработана общими рамками, не отдельными объектами. Поэтому среда также предоставляет параметр анимации к функциям управления цветом.