XMesh, XSubmesh, YMesh, YSubmesh, ZMeshКоличество точек выборки
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
XMesh, XSubmesh, YMesh, YSubmesh, ZMesh | Наследованный | Положительное целое число |
| Объекты | Значения по умолчанию |
|---|---|
plot::Function2d |
|
plot::Function3d |
|
plot::Implicit2d, plot::Raster, plot::VectorField2d |
|
plot::Implicit3d |
|
plot::VectorField3d |
|
plot::Conformal |
|
plot::Inequality |
|
plot::Density |
|
plot::Matrixplot |
|
plot::Listplot |
|
Атрибуты XMesh и т.д. определяют количество точек выборки, используемых для числового приближения объектов графика, таких как функциональные графики, неявные графики и т.д.
Различные типы объектов используют числовые функциональные оценки на дискретной равноотстоящей mesh. XMesh, YMesh, и для plot::Implicit3d также ZMesh устанавливают число точек этой mesh. Исключение этого параметризовано кривые и поверхности, которые используют атрибуты UMesh, USubmesh, VMesh и VSubmesh.
Для большинства упомянутых выше типов объектов интерпретация целых чисел, установленных этими атрибутами, следующие: В каждом XRange, YRange, ZRange, соответствующее число точек распространено equidistantly. Для XMesh = 2 и XRange = 0..1, например, оценка происходит для x = 0 и x = 1. Для XMesh = 3
используется дальнейшая точка mesh в.
Исключением к этому правилу является plot::Implicit2d: Здесь, значения XMesh и YMesh определяют плотность доллара США сетки для нахождения компонентов, и увеличение их значений помогает точно в тех случаях, где компоненты (т.е. строки) отсутствуют в графике. Уменьшение XMesh и YMesh в 2D неявном графике не заставит кривые казаться более грубыми; это может привести к пропавшим без вести кривых.
Для типов, реагирующих на AdaptiveMesh и для plot::Implicit3d, эта mesh используется, чтобы найти начальные значения, которые могут быть усовершенствованы далее. См. документацию определенных типов и AdaptiveMesh для деталей.
В целом более прекрасная mesh (более высокие значения) приводит к более длительному вычислению, в то время как более грубая mesh может вызвать пропускаемые детали.
Можно задать XMesh = nx, YMesh = ny, XSubmesh = mx, YSubmesh = mv также в более короткой Форме Mesh = [nx, ny], Submesh = [mx, my].
Известная функция
колеблется дико около источника. Стандартные значения mesh не достаточны, чтобы разрешить поведение функции около критической точки:
plot(plot::Function2d(sin(1/x), x = -1 .. 1))
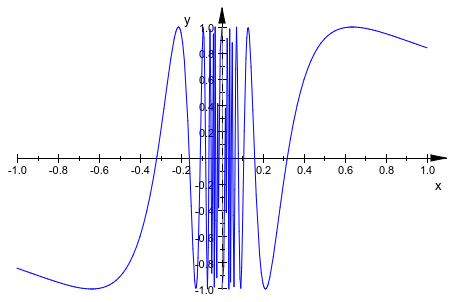
Мы получаем лучший результат с увеличенным значением XMesh:
plot(plot::Function2d(sin(1/x), x = -1 .. 1), XMesh = 1000)
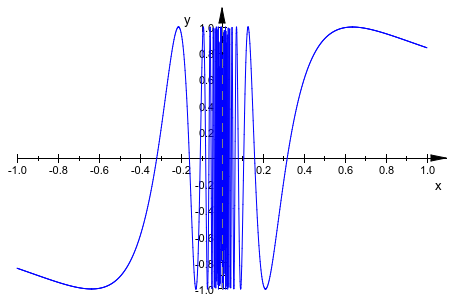
В следующем графике, значениях по умолчанию XMesh, YMesh не достаточен, чтобы произвести достаточно сглаженный функциональный график:
plot(plot::Function3d(besselJ(0, sqrt(x^2 + y^2)),
x = -20 .. 20, y = -20 .. 20)):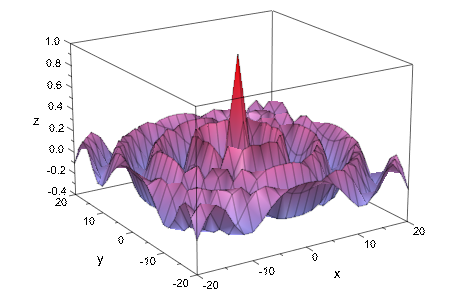
Увеличивая значения по умолчанию XSubmesh = 0, YSubmesh = 0 приводит к более высокому графику разрешения. Обратите внимание на то, что это не влияет на количество строк mesh, которые отображены:
plot(plot::Function3d(besselJ(0, sqrt(x^2 + y^2)),
x = -20 .. 20, y = -20 .. 20,
XSubmesh = 2, YSubmesh = 2)):
Также мы увеличиваем значения XMesh, YMesh и используем значения по умолчанию XSubmesh = 0, YSubmesh = 0. Это, однако, увеличивает число строк mesh, которые отображены:
plot(plot::Function3d(besselJ(0, sqrt(x^2 + y^2)),
x = -20 .. 20, y = -20 .. 20,
XMesh = 73, YMesh = 73)):
Еще одна возможность состоит в том, чтобы использовать значения по умолчанию XMesh, YMesh, XSubmesh, YSubmesh и активировать адаптивный механизм, чтобы сгладить критические области графика. Однако этот график состоит почти полностью из критических областей, и адаптивный механизм поэтому будет медленнее, чем прямое вычисление с более прекрасной mesh, которая приводит почти к тому же результату:
plot(plot::Function3d(besselJ(0, sqrt(x^2 + y^2)),
x = -20 .. 20, y = -20 .. 20,
AdaptiveMesh = 2)):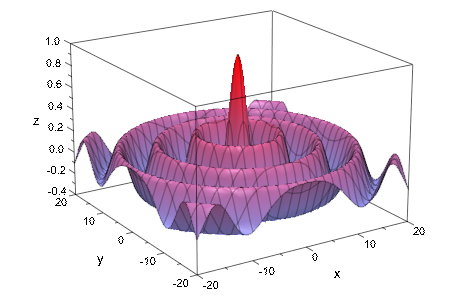
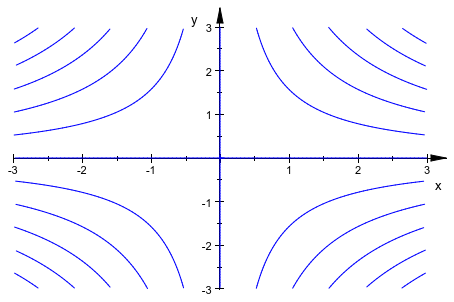
Для двумерных неявных графиков XMesh и YMesh определяют сетку “точек seed”, которые используются, чтобы найти компоненты (дополнительную информацию см. в документации plot::Implicit2d). В действительности это означает, что, если некоторые компоненты отсутствуют в графике, значения этих атрибутов должны быть увеличены:
plot(plot::Implicit2d(sin(2*x*y), x = -3..3, y = -3..3))
plot(plot::Implicit2d(sin(2*x*y), x = -3..3, y = -3..3,
XMesh = 20, YMesh = 20))