polylib:: realrootsИзолируйте все действительные корни действительного одномерного полинома
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
polylib::realroots(p) polylib::realroots(p,eps)
polylib::realroots(p) возвращает интервалы, изолирующие действительные корни действительного одномерного полиномиального p.
polylib::realroots(p, eps) возвращает усовершенствованные интервалы, аппроксимирующие действительные корни p к относительной точности, данной eps.
Все коэффициенты p должны быть действительными и числовыми, т.е. или целые числа, rationals или числа с плавающей запятой. Числовые символьные объекты, такие как sqrt(2), exp(10*PI) и т.д. принят, если они могут быть преобразованы в действительные числа с плавающей запятой через float. То же самое содержит для цели точности eps.
Интервалы изоляции упорядочены таким образом, что их центры увеличиваются, т.е. a i + b i <a i + 1 + b i + 1.
Номер nops(realroots(p)) интервалов является количеством действительных корней p. Несколько корней считаются только однажды. Cf. Пример 3.
Изоляция интервалов может быть довольно большой. eps дополнительного аргумента может использоваться, чтобы совершенствовать интервалы, таким образом, что они аппроксимируют действительные корни к относительной точности eps. С этим аргументом удовлетворяют возвращенные интервалы![]() , т.е. каждый центр
, т.е. каждый центр![]() аппроксимирует корень с относительной точностью
аппроксимирует корень с относительной точностью eps/2.
Некоторую заботу нужно соблюдать при попытке получить очень точные приближения корней через маленькие значения eps. Внутренне, bisectioning с точной рациональной арифметикой используется, чтобы определить местоположение корней к точности eps. Этот процесс может занять намного больше времени, чем определение интервалов изоляции, не используя второй аргумент eps в polylib::realroots. Это может быть быстрее, чтобы использовать умеренные значения eps, чтобы получить первые приближения корней через polylib::realroots. Эти приближения могут затем быть улучшены быстрым числовым решателем, таким как numeric::fsolve с соответственно высоким значением DIGITS. Cf. Пример 6. Однако обратите внимание, что polylib::realroots будет всегда преуспевать в том, чтобы определить местоположение корней к желаемой точности в конечном счете. Числовые решатели могут привести к сбою или возвратить корень, не принадлежащий интервалу, который использовался для начального приближения.
Неожиданные результаты могут быть получены, когда полином содержит иррациональные коэффициенты. Внутренне, любой такой коэффициент c преобразован в число с плавающей запятой. Это плавание затем заменяется рациональным числом приближения удовлетворение r![]() . Наконец,
. Наконец, polylib::realroots возвращает строгие границы для действительных корней рационализированного полинома. Несмотря на то, что все коэффициенты аппроксимированы правильно к десятичным разрядам DIGITS, это может изменить корни решительно. В частности, несколько корней или кластеров плохо разделенных простых корней очень чувствительны к небольшим возмущениям в коэффициентах полинома. Смотрите Пример 4 и Пример 5.
Функция чувствительна к переменной окружения DIGITS, если существует нецелое число или нерациональные коэффициенты в полиноме. Любой такой коэффициент заменяется рациональным числом, аппроксимирующим коэффициент к DIGITS значительные десятичные разряды.
Мы используем многочленное выражение в качестве входа к polylib::realroots:
p := (x - 1/3)*(x - 1)*(x - 4/3)*(x - 2)*(x - 17):
polylib::realroots(p)
![]()
Корни 1 и 2 найдены точно: соответствующие интервалы имеют длину 0. Другие интервалы изоляции являются довольно большими. Мы совершенствовали интервалы, таким образом, что они аппроксимируют корни к 12 десятичным разрядам. Обратите внимание на то, что это независимо от текущего значения DIGITS, потому что никакая арифметика с плавающей точкой не используется:
polylib::realroots(p, 10^(-12))

Мы преобразовываем эти точные границы для действительных корней к приближениям с плавающей точкой. Обратите внимание на то, что со значением по умолчанию DIGITS=10 мы игнорируем 2 из 12 правильных цифр, которые могли потенциально дать рациональные границы:
map(%, map, float)
![]()
delete p:
Ортогональные полиномы степени n имеют n простые действительные корни. Мы считаем Полином лежандра степени 5, доступным в библиотеке orthpoly для ортогональных полиномов:
polylib::realroots(orthpoly::legendre(5, x), 10^(-DIGITS)):
map(%, float@op, 1)
![]()
Мы рассматриваем полином с корнем кратного:
p := poly((x - 1/3)^3*(x - 1), [x])
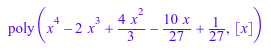
Обратите внимание на то, что только один интервал изоляции [ 0, 1] возвращен для тройного корня![]() :
:
polylib::realroots(p)
![]()
delete p:
Мы рассматриваем полином с нерациональными корнями:
p := (x - 3)^2*(x - PI)^2:
Преобразование результата polylib::realroots к числам с плавающей запятой, каждый видит, что точные корни 3, 3, PI, PI аппроксимированы только к 3 десятичным разрядам:
map(polylib::realroots(p, 10^(-10)), map, float)
![]()
Это вызывается внутренней рационализацией коэффициентов p.
Интервалы, возвращенные polylib::realroots(p, 10^(-10)) правильно, определяют местоположение 4 точных корней этого рационализированного полинома к точности 10 цифр. Однако, потому что все 4 корня близки, небольшие возмущения коэффициентов, введенных рационализацией, имеют решительный эффект на местоположение корней. В частности, рационализация разделяет два исходных двойных корня в 4 простых корня.
delete p:
Мы считаем дальнейший пример включающими неточными коэффициентами. Сначала мы аппроксимируем корни полинома с точными коэффициентами:
p1 := (x - 1/3)^3*(x - 4/3):
map(polylib::realroots(p1, 10^(-10)), map, float)
![]()
Теперь мы вводим ошибки округления, заменяя одну запись приближением с плавающей точкой:
p2 := (x - 1.0/3)^3*(x - 4/3):
map(polylib::realroots(p2, 10^(-10)),map,float)
![]()
В этом примере рационализация заставила тройной корневой 1/3 разделять в один действительный корень и два комплексно-сопряженных корня.
delete p1, p2:
Мы хотим аппроксимировать корни к точности 1 000 цифр:
p := x^5 - 129/20*x^4 + 69/5*x^3 - 14*x^2 + 12*x - 8:
Мы рекомендуем не получить результат непосредственно polylib::realroots(p,10^(-1000)), потому что внутренний bisectioning процесс для совершенствования грубой изоляции интервалов сходится только линейно. Вместо этого мы вычисляем первые приближения корней к точности 10 цифр:
approx := map(polylib::realroots(p, 10^(-10)), float@op, 1)
![]()
Эти значения используются в качестве отправных точек для числового корневого средства поиска. Внутренний поиск Ньютона в numeric::fsolve сходится квадратично и уступает, высокая точность заканчивается намного быстрее, чем polylib::realroots:
DIGITS := 1000:
roots := map(approx, x0 -> numeric::fsolve([p = 0], [x = x0]))
[[x = 1.489177598846870281338916114673844643894...],
[x = 1.752191733304413195335101727880090131407...],
[x = 3.255184555797733438479691333705558491124...]]delete approx, DIGITS, roots, x0:
|
Одномерный полином: или выражение или polyomial доменного типа |
|
(Небольшое) положительное вещественное число, определяющее размер возвращенных интервалов. |
Список списков [[a 1, b 1], [a 2, b 2], …] с рациональными числами a i ≤ b i возвращен. Списки с a i = b i представляют точные рациональные корни. Списки с a i <b i представляют открытые интервалы, содержащие точно один действительный корень. Если полином не имеет никаких действительных корней, то пустой список [ ] возвращен.