числовой::Числовые корни одномерного полинома
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
numeric::polyroots(eqs, <FixedPrecision>, <SquareFree>, <Factor>, <NoWarning>)
numeric::polyroots(eqs) возвращает числовые приближения всех действительных и комплексных корней одномерных полиномов eqs.
Коэффициенты могут быть вещественными или комплексными числами. Также символьные коэффициенты приняты, если они могут быть преобразованы в плавания.
Тривиальный полиномиальный eqs = 0 результатов в сообщении об ошибке. Пустой список возвращен для постоянных полиномов eqs ≠ 0.
Несколько корней перечислены согласно их кратности, т.е. длина корневого списка совпадает со степенью eqs.
Корневой список сортируется по numeric::sort.
Чтобы округлить эффекты, числовые корни должны быть с точностью до DIGITS значительными цифрами, если опция FixedPrecision не используется.
Все записи с плавающей точкой в eqs внутренне аппроксимированы рациональными числами: numeric::polyroots(eqs) вычисляет корни numeric::rationalize(eqs, Minimize).
Для многочленных выражений в учтенной форме числовой поиск применяется к каждому фактору отдельно.
Рекомендуется использовать numeric::realroots или polylib::realroots, если eqs является действительным полиномом, и только действительные корни представляют интерес.
Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Оба многочленных выражения, а также объекты DOM_POLY могут использоваться, чтобы задать полином:
numeric::polyroots(x^3 - 3*x - sqrt(2))
numeric::polyroots(PI*z^4 + I*z + 0.1)
numeric::polyroots(poly(x^5 - x^2, [x]))
Следующий полином имеет точные коэффициенты:
p := poly((x - 1)*(x - PI)^3, [x]): numeric::polyroots(p)
Обратите внимание на то, что ошибки округления в коэффициентах eqs имеют сильное воздействие на нескольких корнях:
p := poly((x - 1.0)*(x - float(PI))^3, [x]): numeric::polyroots(p)
Это корни следующего рационализированного полинома:
numeric::rationalize(p, Minimize)
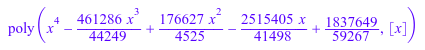
delete p:
Несколько корень
следующего полинома могут только быть вычислены с ограниченной точностью фиксированной арифметикой точности:
p := poly((x^2 - 6*x +8)*(x - I/3)^5, [x]): numeric::polyroots(p, FixedPrecision)
Без опции FixedPrecision рабочая точность увеличена внутренне, чтобы вычислить лучшие приближения:
numeric::polyroots(p)
delete p:
Следующий полином плохо разделил корни. numeric::polyroots не удается разделить их правильно:
p := poly(_mult((x - 1 - i/10^9) $ i=0..5), [x]): numeric::polyroots(p)
Можно предварительно обработать полином символьной факторизацией:
numeric::polyroots(p, Factor)
Также можно увеличить рабочую точность, чтобы разделить корни:
DIGITS := 20: numeric::polyroots(p)
delete p, DIGITS:
|
Одномерное многочленное выражение или одномерный полином доменного типа |
|
Эта опция обеспечивает самый быстрый способ получить приближения корней числовым поиском с фиксированной внутренней точностью 2 DIGITS десятичные разряды. Обратите внимание на то, что плохо изолированные корни или несколько корней не будут обычно аппроксимироваться к десятичным числам Без этой опции |
|
При использовании этой опции символьная квадратная свободная факторизация вычисляется через Эта опция рекомендуется, когда Для полиномов с действительными рациональными коэффициентами всегда используется квадратная свободная факторизация, т.е. эта опция не имеет никакого эффекта для таких полиномов. Для всех других типов коэффициентов квадратная свободная факторизация может быть дорогостоящей и должна требоваться этой опцией. С несколькими корнями |
|
При использовании этой опции вычисляются символьные факторизации Эта опция полезна, когда |
|
Отключает предупреждения |
Список числовых корней.
Числовой корневой алгоритм нахождения, реализованный numeric::polyroots, является методом Лагерра: В.Х. Пресс, B.P. Flannery, S.A. Теукольский и В.Т. Веттерлинг: Числовые Рецепты в C, издательстве Кембриджского университета, 1988.
