potential(Скалярный) потенциал поля градиента
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
potential(f, [x1, x2, …], <[y1, y2, …]>, <Test>)
potential(f, x) определяет, является ли векторное поле
полем градиента
некоторого скалярного потенциального p относительно переменных 
и вычисляет тот потенциал, если это существует.
Потенциал векторного поля
= [f 1 (x 1, x 2, …), f 2 (x 1, x 2, …), …] существует (локально), если и только если якобиевская матрица
симметрична в i и j. На 3 пробелах это - условие, которое
исчезает.
Потенциал
с
исключительно определяется до аддитивной постоянной.
Интегральным представлением потенциала дают
,
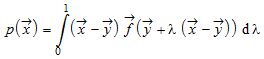где
произвольная “базисная точка”. Это - криволинейный интеграл
вдоль прямой линии от
к
.
Если якобиевская матрица
не симметрична, потенциал
не существует. В этом случае potential возвращает FALSE.
Обратите внимание на то, что ответ FALSE не всегда окончателен. Для произвольных выражений f i, f j, нет никакого алгоритма, чтобы решить, содержит ли
математически: potential может возвратить FALSE из-за недостаточного упрощения частных производных.
Представление потенциала зависит на основании символьного интегратора int. Если int не удается найти, что закрытая форма потенциальных, символьных вызовов int может быть возвращена. Смотрите Пример 3.
Если никакая базисная точка
не задана, потенциал только задан до некоторой аддитивной постоянной.
potential не рассматривает вопросы неоднородности векторного поля и его потенциала и исследует потенциал только локально. Возвращенный потенциал может быть допустимым потенциалом только в районе текущей точки
!
Если f является вектором, звонок компонента f должен быть полем (т.е. область категории Cat::Field), который позволяет интегрирование.
Используя опцию Test, мы проверяем, является ли векторное поле полем градиента:
f := [x, y, z*exp(z)]: potential(f, [x, y, z], Test)
Без опции Test возвращен потенциал:
potential(f, [x, y, z])
Мы проверяем результат:
normal(gradient(%, [x, y, z]))
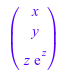
Когда 'базисная точка' задана, подходящая константа добавляется к потенциалу, таким образом, что это исчезает в этой точке:
potential(f, [x, y, z], [0, 0, 0])
potential(f, [x, y, z], [x0, y0, z0])
delete f:
Векторное поле в этом примере не является полем градиента и не имеет никакого потенциала:
potential([x[2], -x[1]], [x[1], x[2]])
Векторное поле в этом примере является полем градиента и имеет потенциал. Однако символьный интегратор не находит закрытую форму интегрального представления для потенциала и возвращает символьный определенный интеграл:
potential([a + b*x, sin(y^2)*exp(y)], [x, y])
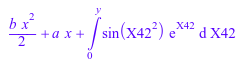
Мы проверяем результат:
gradient(%, [x, y])
|
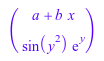
Векторное поле: список арифметических выражений или вектор таких выражений. Вектором является n ×1 или 1 ×n матрица области категории |
|
Переменные: идентификаторы или индексированные идентификаторы |
|
Компоненты “базисной точки”: арифметические выражения. Если базисная точка |
|
Проверяйте, имеет ли векторное поле потенциал, и возвратите |
Арифметическое выражение или булево значение.
