`статистика::`

Качество подгонки Шапиро-Вилка тестирует на нормальность

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

stats::swGOFT(x₁, x₂, …)
stats::swGOFT([x₁, x₂, …])
stats::swGOFT(s, <c>)

Описание

stats::swGOFT ([x ₁, x ₂, …]) применяет тест качества подгонки Шапиро-Вилка для нулевой гипотезы: “данные x ₁, x ₂, … нормально распределен (с неизвестным средним значением и отклонением)”. Объем выборки не должен быть больше, чем 5 000 и не меньшим, чем 3.

Внешние статистические данные, сохраненные в ASCII-файле, могут быть импортированы в сеанс MuPAD^® через import::readdata. В частности, смотрите Пример 1 из соответствующей страницы справки.

Ошибка повышена stats::swGOFT, если какие-либо из данных не могут быть преобразованы в действительное число с плавающей запятой или если объем выборки является слишком большим или слишком маленьким.

Позвольте y ₁, …, y _n быть входными данными x ₁, …, x _n, расположенный в порядке возрастания. stats::swGOFT возвращает список [PValue = p, StatValue = w], содержащий следующую информацию:

w является достигнутым значением статистической величины Шапиро-Вилка

.

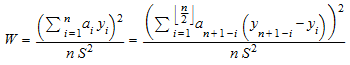Здесь, _i a является коэффициентами Шапиро-Вилка, и S^2 является статистическим отклонением выборки.
p является наблюдаемым уровнем значения статистической величины Шапиро-Вилка W.

Наблюдаемый уровень значения PValue = p, возвращенный stats::swGOFT, должен быть интерпретирован следующим образом: Если p меньше, чем данный уровень значения α <<1, нулевая гипотеза может быть отклонена на уровне α. Если p больше, чем α, нулевая гипотеза не должна быть отклонена на уровне α.

Взаимодействия среды

Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.

Примеры

Пример 1

Мы тестируем список случайных данных, которые подразумевают быть выборкой нормально распределенных чисел:

f := stats::normalRandom(0, 1, Seed = 123):
data := [f() $ i = 1..400]:
stats::swGOFT(data)

Наблюдаемый уровень значения не является небольшим. Следовательно, не нужно отклонять нулевую гипотезу, что данные нормально распределены.

Затем, мы любим до безумия данные с некоторыми однородно непрерывными, отклоняется:

impuredata := data . [frandom() $ i = 1..101]:
stats::swGOFT(impuredata)

Любившие до безумия данные могут быть отклонены как выборка нормальных отклонений на уровнях значения, столь же небольших как.

delete f, data, impuredata:

Пример 2

Мы создаем выборку, состоящую из одного столбца строки и двух столбцов нестроки:

s := stats::sample(
   [["1996", 1242, PI - 1/2],
    ["1997", 1353, PI + 0.3], 
    ["1998", 1142, PI + 0.5], 
    ["1999", 1201, PI - 1], 
    ["2001", 1201, PI]
   ])

"1996"  1242  PI - 1/2
"1997"  1353  PI + 0.3
"1998"  1142  PI + 0.5
"1999"  1201    PI - 1
"2001"  1201        PI

Мы проверяем, нормально распределены ли данные третьего столбца:

stats::swGOFT(s, 3)

Наблюдаемый уровень значения, возвращенный тестом, не является небольшим: тест не указывает, что данные не нормально распределены.

delete s:

Параметры

`_{x1, x2, …}`	Статистические данные: действительные численные значения
`s`	Выборка доменного типа `stats::sample`
`c`	Целое число, представляющее индекс столбца демонстрационного `s`. Этот столбец предоставляет данным x ₁, x ₂ и т.д. Нет никакой потребности задать номер столбца `c`, если выборка имеет только один столбец.

Возвращаемые значения

Список двух уравнений [PValue = p, StatValue = w] со значениями с плавающей точкой p и w. Смотрите раздел 'Details' ниже для интерпретации этих значений.

Алгоритмы

Реализованный алгоритм для вычисления коэффициентов Шапиро-Вилка, статистической величины Шапиро-Вилка и наблюдаемого уровня значения на основе: Патрик Ройстон, “Алгоритм, КОГДА R94”, Прикладная статистика, Vol.44, № 4 (1995).

После Ройстона, коэффициенты Шапиро-Вилка a _i вычисляются приближением

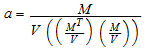
где M обозначает ожидаемые значения стандартной нормальной статистической величины порядка для выборки, V является соответствующей ковариационной матрицей и M^{, T} является транспонированием M.

Документация