статистика::T-тест для среднего значения
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
stats::tTest(x1, x2, …,m, <Normal>) stats::tTest([x1, x2, …],m, <Normal>) stats::tTest(s, <c>,m, <Normal>)
stats::tTest( [x1, x2, …], m ) тестирует нулевую гипотезу: “истинное среднее значение данных x i больше, чем m”.
stats::tTest принимает числовые данные, а также символьные данные.
Если все данные являются действительными числами с плавающей запятой, возвращенные значения, p и t являются числами с плавающей запятой.
Если m является числом с плавающей запятой, выборочные данные преобразованы в числа с плавающей запятой автоматически.
Для демонстрационного x 1, x 2, … размера n, stats::tTest вычисляет
, где
эмпирическое среднее значение данных и
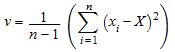
эмпирическое отклонение.
stats::tTest(data, m) возвращает список [PValue = p, StatValue = t], где наблюдаемый уровень значения p вычисляется как p = stats::tCDF (n - 1)(t).
stats::tTest(data, m, Normal) возвращает список [PValue = p, StatValue = t], где наблюдаемый уровень значения p вычисляется как p = stats::normalCDF (0, 1)(t). Для большого n это - приближение stats::tCDF (n - 1)(t).
Интуитивно, p соответствует “вероятности”, что истинное среднее значение данных (значение ожидания базового распределения) больше, чем m.
Наиболее релевантная информация, возвращенная stats::tTest, является наблюдаемым уровнем значения PValue = p. Это должно быть интерпретировано следующим образом:
T-тест может использоваться в качестве одностороннего теста нулевой гипотезы: “истинное среднее значение данных больше, чем m”. В этом случае нулевая гипотеза может быть отклонена на уровне α, если наблюдаемый уровень значения p удовлетворяет p <α.
Также t-тест может также использоваться в качестве одностороннего теста нулевой гипотезы: “истинное среднее значение данных меньше, чем m”. В этом случае нулевая гипотеза может быть отклонена на уровне α, если наблюдаемый “уровень значения” p удовлетворяет p> 1 - α.
Также t-тест может также использоваться в качестве двустороннего теста нулевой гипотезы: “истинным средним значением данных является m”. Если наблюдаемый “уровень значения” p, возвращенный stats::tTest, удовлетворяет или
или
для некоторого данного уровня 0 <α <1, эта нулевая гипотеза может быть отклонена на уровне α.
Внешние статистические данные, сохраненные в ASCII-файле, могут быть импортированы в сеанс MuPAD® через import::readdata. В частности, смотрите Пример 1 из соответствующей страницы справки.
Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
10 экспериментов произвели значения 1, - 2, 3, - 4, 5, - 6, 7, - 8, 9, 10, которые приняты, чтобы быть нормально распределенными с неизвестным средним значением и отклонением. Эмпирическое среднее значение выборочных данных 1.5. Существует только маленькая вероятность p =
, что истинное среднее значение больше, чем 5,0:
data := [1, -2, 3, -4, 5, -6, 7, -8, 9, 10]: stats::tTest(data, 5.0)
Мы сравниваем этот результат с наблюдаемым уровнем значения, вычисленным через стандартное нормальное распределение:
stats::tTest(data, 5.0, Normal)
Приближение наблюдаемого уровня значения p стандартным нормальным распределением довольно плохо из-за размера небольшой выборки. Затем, мы рассматриваем большую выборку. Истинное среднее значение случайных данных должно быть 10:
r := stats::normalRandom(10, 12, Seed = 0): data := [r() $ i = 1..100]: stats::tTest(data, 10);
stats::tTest(data, 10, Normal)
С наблюдаемым уровнем значения p =
, данные не дисквалифицированы как наличие истинного среднего значения 10. Для выборок этого размера нормальное распределение аппроксимирует t-распределение хорошо.
delete data, r:
|
Статистические данные: арифметические выражения |
|
Оценка для истинного среднего значения данных: арифметическое выражение |
|
Выборка доменного типа |
|
Целое число, представляющее индекс столбца демонстрационного |
|
Вычислите наблюдаемый уровень значения стандартным нормальным распределением вместо t-распределения. |
список двух уравнений [PValue = p, StatValue = t] с численными значениями p и t. Смотрите раздел 'Details' ниже для интерпретации этих значений.
Если отклонение данных исчезает, FAIL возвращен.
Если данные нормально распределены со значением ожидания ('истинное среднее значение') μ, переменная
является t-distributed с n - 1 степень свободы. Вероятностью события, что T достигает значений, не больше, чем t, является Pr (T ≤ t) =stats::tCDF(n - 1)(t).