Решите уравнения численно

Symbolic Math Toolbox™ предлагает и числовые и символьные решатели уравнения. Для сравнения числовых и символьных решателей смотрите, Выбирают Numeric or Symbolic Solver. Уравнение или система уравнений могут иметь несколько решений. Чтобы найти эти решения численно, используйте функциональный vpasolve. Для полиномиальных уравнений vpasolve возвращает все решения. Для неполиномиальных уравнений vpasolve возвращает первое решение, которое он находит. Это показывает вам, как использовать vpasolve, чтобы найти решения и полиномиальных и неполиномиальных уравнений, и как получить эти решения произвольной точности.

Найдите все корни полиномиальной функции
Найдите нули неполиномиальной функции Используя поисковые области значений и отправные точки
Получите решения произвольной точности
Решите многомерные уравнения Используя поисковые области значений

Найдите все корни полиномиальной функции

Используйте vpasolve, чтобы найти все решения функционировать $f (x) = 6 x^{7} - 2 x^{6} + 3 x^{3} - 8$ .

syms f(x)
f(x) = 6*x^7-2*x^6+3*x^3-8;
sol = vpasolve(f)

sol =
                                          1.0240240759053702941448316563337
 - 0.88080620051762149639205672298326 + 0.50434058840127584376331806592405i
 - 0.88080620051762149639205672298326 - 0.50434058840127584376331806592405i
 - 0.22974795226118163963098570610724 + 0.96774615576744031073999010695171i
 - 0.22974795226118163963098570610724 - 0.96774615576744031073999010695171i
    0.7652087814927846556172932675903 + 0.83187331431049713218367239317121i
    0.7652087814927846556172932675903 - 0.83187331431049713218367239317121i

vpasolve возвращает семь корней функции, как ожидалось, потому что функция является полиномом степени семь.

Найдите нули неполиномиальной функции Используя поисковые области значений и отправные точки

Рассмотрите функцию $f (x) = e^{(x / 7)} потому что (2 x)$ . График функции показывает периодические нули с увеличением наклонов в нулевых точках, когда x увеличивается.

syms x
h = fplot(exp(x/7)*cos(2*x),[-2 25]);
grid on

Используйте vpasolve, чтобы найти нуль функционального f. Обратите внимание на то, что vpasolve возвращает только одно решение неполиномиального уравнения, даже если существуют несколько решений. На повторных вызовах vpasolve возвращает тот же результат, даже если существуют несколько нулей.

f = exp(-x/20)*cos(2*x);
for i = 1:3
	vpasolve(f,x)
end

ans =
19.634954084936207740391521145497
ans =
19.634954084936207740391521145497
ans =
19.634954084936207740391521145497

Чтобы найти несколько решений, установите опцию random на true. Это заставляет vpasolve выбрать отправные точки случайным образом. Для получения информации об алгоритме, который выбирает случайные отправные точки, см. Алгоритмы на странице vpasolve.

for i = 1:3
		vpasolve(f,x,'random',true)
end

ans =
-226.98006922186256147892598444194
ans =
98.174770424681038701957605727484
ans =
58.904862254808623221174563436491

Чтобы найти нуль близко к x = 10 и к x = 1000, установите отправную точку 10, и затем 1000.

vpasolve(f,x,10)
vpasolve(f,x,1000)

ans =
10.210176124166828025003590995658
ans =
999.8118620049516981407362567287

Найти нуль в области значений $15 \leq x \leq 25$ , установите поисковую область значений на [15 25].

vpasolve(f,x,[15 25])

ans =
21.205750411731104359622842837137

Чтобы найти несколько нулей в области значений [15 25], вы не можете неоднократно вызывать vpasolve, когда это возвращает тот же результат на каждом вызове, как ранее показано. Вместо этого установите random на true в сочетании с поисковой областью значений.

for i = 1:3
vpasolve(f,x,[15 25],'random',true)
end

ans =
21.205750411731104359622842837137
ans =
16.493361431346414501928877762217
ans =
16.493361431346414501928877762217

Если вы задаете опцию random, также задавая отправную точку, vpasolve предупреждает вас, что эти две опции несовместимы.

vpasolve(f,x,15,'random',true)

Warning: 'Random' has no effect because
 all variables have a starting value. 
> In sym/vpasolve (line 168) 
ans =
14.922565104551517882697556070578

Создайте функциональный findzeros ниже, чтобы систематически найти все нули для f в данной поисковой области значений в ошибочном допуске. Это запускается с входной области значений поиска и вызывает vpasolve, чтобы найти нуль. Затем это разделяет поисковую область значений в два вокруг значения нуля, и рекурсивно вызывает себя с новыми поисковыми областями значений как входные параметры, чтобы найти больше нулей. Первый вход является функцией, второй вход является областью значений, и дополнительный третий вход позволяет вам задавать ошибку между нулем и верхними и нижними границами, сгенерированными от него.

Функции объясняют раздел разделом здесь.

Объявите функцию с двумя входными параметрами и одним выводом.

function sol = findzeros(f,range,err)

Если вы не задаете дополнительный аргумент для ошибочного допуска, findzeros устанавливает err на 0.001.

if nargin < 2
    err = 1e-3;
end

Найдите нуль в поисковой области значений с помощью vpasolve.

sol = vpasolve(f,range);

Если vpasolve не находит нуль, выход.

if(isempty(sol))
    return

Если vpasolve находит нуль, разделите поисковую область значений в две поисковых области значений выше и ниже нуля.

else
    lowLimit = sol-err;
    highLimit = sol+err;

Вызовите findzeros с более низкой поисковой областью значений. Если findzeros возвращает нули, скопируйте значения в массив решения и отсортируйте их.

    temp = findzeros(f,[range(1) lowLimit],1);
    if ~isempty(temp)
        sol = sort([sol temp]);
    end

Вызовите findzeros с более высокой поисковой областью значений. Если findzeros возвращает нули, скопируйте значения в массив решения и отсортируйте их.

    temp = findzeros(f,[highLimit range(2)],1);
    if ~isempty(temp)
        sol = sort([sol temp]);
    end
    return
end
end

Целая функция findzeros следующие.

function sol = findzeros(f,range,err)
if nargin < 3
    err = 1e-3;
end
sol = vpasolve(f,range);
if(isempty(sol))
    return
else
    lowLimit = sol-err;
    highLimit = sol+err;
    temp = findzeros(f,[range(1) lowLimit],1);
    if ~isempty(temp)
        sol = sort([sol temp]);
    end
    temp = findzeros(f,[highLimit range(2)],1);
    if ~isempty(temp)
        sol = sort([sol temp]);
    end
    return
end
end

Вызовите findzeros с поисковой областью значений [10 20], чтобы найти все нули в той области значений для f(x) = exp(-x/20)*cos(2*x) в ошибочном допуске по умолчанию.

syms f(x)
f(x) = exp(-x/20)*cos(2*x);
findzeros(f,[10 20])

ans =
[ 10.210176124166828025003590995658, 11.780972450961724644234912687298,...
 13.351768777756621263466234378938, 14.922565104551517882697556070578,...
 16.493361431346414501928877762217, 18.064157758141311121160199453857,...
 19.634954084936207740391521145497]

Получите решения произвольной точности

Используйте digits, чтобы установить точность решений. По умолчанию vpasolve возвращает решения точности 32 значащих цифр. Используйте digits, чтобы увеличить точность до 64 значащих цифр. При изменении digits гарантируйте, что вы сохраняете его текущее значение так, чтобы можно было восстановить его.

f = exp(x/7)*cos(2*x);
vpasolve(f)
digitsOld = digits;
digits(64)
vpasolve(f)
digits(digitsOld)

ans =
-7.0685834705770347865409476123789
ans =
-7.068583470577034786540947612378881489443631148593988097193625333

Решите многомерные уравнения Используя поисковые области значений

Рассмотрите следующую систему уравнений.

$\begin{array}{l} z = 10 (потому что (x) + потому что (y)) \\ z = x + y^{2} - 0.1 x^{2} y \\ x + y - 2.7 = 0 \end{array}$

График уравнений для 0 ≤ x ≤ 2,5 и 0 ≤ x ≤ 2.5 показывает, что три поверхности пересекаются в двух точках. Чтобы лучше визуализировать график, используйте view. Чтобы масштабировать значения палитры, используйте caxis.

syms x y z
eqn1 = z == 10*(cos(x) + cos(y));
eqn2 = z == x+y^2-0.1*x^2*y;
eqn3 = x+y-2.7 == 0;
equations = [eqn1 eqn2 eqn3];
fimplicit3(equations)
axis([0 2.5 0 2.5 -20 10])
title('System of Multivariate Equations')
view(69, 28)
caxis([-15 10])

Используйте vpasolve, чтобы найти точку, где поверхности пересекаются. Функциональный vpasolve возвращает структуру. Чтобы получить доступ к решению, индексируйте в структуру.

sol = vpasolve(equations);
[sol.x sol.y sol.z]

ans =  $(\begin{matrix} 2.3697477224547979209101337160174 & 0.33025227754520207908986628398261 & 2.2933543768232277431243854708612 \end{matrix})$

Чтобы искать область пробела решения, задайте поисковые области значений для переменных. Если вы задаете области значений $0 \leq x \leq 1.5$ и $1.5 \leq y \leq 2.5$ , затем функция vpasolve ищет ограниченную область, показанную в изображении.

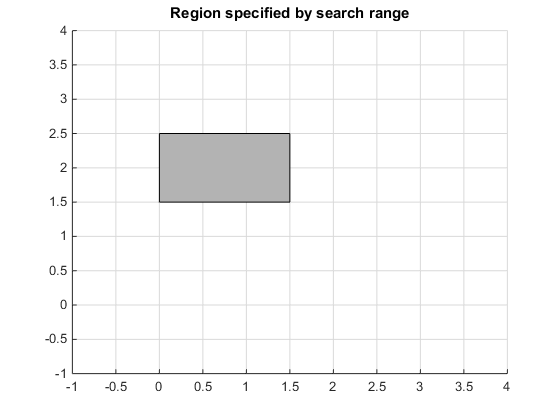
Используйте vpasolve, чтобы найти решение для этой поисковой области значений $0 \leq x \leq 1.5$ и $1.5 \leq y \leq 2.5$ . Чтобы не использовать поисковую область значений для z, установите поисковую область значений на [NaN NaN].

vars = [x y z];
range = [0 1.5; 1.5 2.5; NaN NaN];
sol = vpasolve(equations, vars, range);
[sol.x sol.y sol.z]

ans =  $(\begin{matrix} 0.91062661725633361176950031551069 & 1.7893733827436663882304996844893 & 3.9641015721356254724107884666807 \end{matrix})$

Чтобы найти несколько решений, можно установить опцию random на true. Это заставляет vpasolve использовать случайные отправные точки на последовательных выполнениях. Опция random может использоваться в сочетании с поисковыми областями значений, чтобы заставить vpasolve использовать случайные отправные точки в поисковой области значений. Поскольку random выбирает отправные точки случайным образом, то же решение может быть найдено на последовательных вызовах. Вызовите vpasolve неоднократно, чтобы гарантировать, что вы находите оба решения.

clear sol
range = [0 3; 0 3; NaN NaN];
for i = 1:5
    temp = vpasolve(equations, vars, range, 'random', true);
	sol(i,1) = temp.x;
    sol(i,2) = temp.y;
    sol(i,3) = temp.z;
end
sol

sol = 
 $(\begin{matrix} 0.91062661725633361176950031551069 & 1.7893733827436663882304996844893 & 3.9641015721356254724107884666807 \\ 2.3697477224547979209101337160174 & 0.33025227754520207908986628398261 & 2.2933543768232277431243854708612 \\ 0.91062661725633361176950031551069 & 1.7893733827436663882304996844893 & 3.9641015721356254724107884666807 \\ 0.91062661725633361176950031551069 & 1.7893733827436663882304996844893 & 3.9641015721356254724107884666807 \\ 0.91062661725633361176950031551069 & 1.7893733827436663882304996844893 & 3.9641015721356254724107884666807 \end{matrix})$

Постройте уравнения. Наложите решения как график рассеивания точек с желтыми маркерами X с помощью scatter3. Чтобы лучше визуализировать график, сделайте две из поверхностей прозрачным использованием alpha. Масштабируйте палитру к значениям графика с помощью caxis и измените перспективу с помощью view.

vpasolve находит решения на пересечении поверхностей сформированными уравнениями как показано.

clf
ax = axes;
h = fimplicit3(equations);
h(2).FaceAlpha = 0;
h(3).FaceAlpha = 0;
axis([0 2.5 0 2.5 -20 10])
hold on
scatter3(sol(:,1),sol(:,2),sol(:,3),600,'yellow','X','LineWidth',2)
title('Randomly found solutions in specified search range')
cz = ax.Children;
caxis([0 20])
view(69,28)
hold off

Документация