Exponenta Banner

dwt

Одноуровневый 1D дискретный вейвлет преобразовывает

свернуть все на странице

Синтаксис

[cA,cD] = dwt(x,wname)
[cA,cD] = dwt(x,LoD,HiD)
[cA,cD] = dwt(___,'mode',extmode)

Описание

пример

[cA,cD] = dwt(x,wname) возвращает одноуровневый дискретный вейвлет преобразовывает (DWT) векторного x с помощью вейвлета, заданного wname. Вейвлет должен быть распознан wavemngr. dwt возвращает содействующий вектор приближения cA и содействующий вектор детали cD DWT.

Примечание

Если ваше приложение требует многоуровневого разложения вейвлета, рассмотрите использование wavedec.

пример

[cA,cD] = dwt(x,LoD,HiD) возвращает одноуровневый DWT, использование масштабирования (lowpass) фильтрует LoD, и вейвлет (highpass) фильтруют HiD. Фильтры должны иметь ту же ровную длину.

[cA,cD] = dwt(___,'mode',extmode) возвращает одноуровневый DWT с заданным дополнительным режимом extmode. Для получения дополнительной информации смотрите dwtmode.

Примеры

свернуть все

Скрипт Open Live Script

Получите одноуровневый DWT шумного Доплеровского сигнала использование имени вейвлета. 

load noisdopp;
[cA,cD] = dwt(noisdopp,'sym4');

Восстановите сглаживавшую версию сигнала с помощью коэффициентов приближения. Постройте и сравните с исходным сигналом.

xrec = idwt(cA,zeros(size(cA)),'sym4');
plot(noisdopp)
hold on
grid on
plot(xrec)
legend('Original','Reconstruction')

Скрипт Open Live Script

Получите одноуровневый DWT шумного Доплеровского сигнала использование вейвлета (highpass) и масштабирование (lowpass) фильтры. 

load noisdopp;
[LoD,HiD] = wfilters('bior3.5','d');
[cA,cD] = dwt(noisdopp,LoD,HiD);

Создайте набор фильтров DWT, который может быть применен к шумному Доплеровскому сигналу использование того же вейвлета. Получите highpass и фильтры lowpass от набора фильтров.

len = length(noisdopp);
fb = dwtfilterbank('SignalLength',len,'Wavelet','bior3.5');
[lo,hi] = filters(fb);

Для вейвлета bior3.5 lo и hi являются 12 2 матрицами. lo является фильтрами lowpass, и hi является фильтрами highpass. Первые столбцы lo и hi используются для анализа, и вторые столбцы используются для синтеза. Сравните первый столбец lo и hi с LoD и HiD соответственно. Подтвердите, что они равны.

disp('Lowpass Analysis Filters')
Lowpass Analysis Filters

[lo(:,1) LoD']
ans = 12×2

   -0.0138   -0.0138
    0.0414    0.0414
    0.0525    0.0525
   -0.2679   -0.2679
   -0.0718   -0.0718
    0.9667    0.9667
    0.9667    0.9667
   -0.0718   -0.0718
   -0.2679   -0.2679
    0.0525    0.0525
      ⋮


disp('Highpass Analysis Filters')
Highpass Analysis Filters

[hi(:,1) HiD']
ans = 12×2

         0         0
         0         0
         0         0
         0         0
   -0.1768   -0.1768
    0.5303    0.5303
   -0.5303   -0.5303
    0.1768    0.1768
         0         0
         0         0
      ⋮

Постройте односторонние частотные характеристики значения вейвлета первого уровня и масштабирующихся фильтров.

[psidft,f,phidft] = freqz(fb);
level = 1;
plot(f(len/2+1:end),abs(phidft(level,len/2+1:end)))
hold on
plot(f(len/2+1:end),abs(psidft(level,len/2+1:end)))
grid on
legend('Scaling Filter','Wavelet Filter')
title('First-Level One-sided Frequency Responses')
xlabel('Normalized Frequency (cycles/sample)')
ylabel('Magnitude')

Входные параметры

свернуть все

Входные данные, заданные как вектор с действительным знаком.

Типы данных: double

Анализ вейвлета, используемого к вычислению одноуровневого DWT, заданного как вектор символов или скаляр строки. Вейвлет должен быть распознан wavemngr. Вейвлет анализа от одного из следующих семейств вейвлетов: Daubechies, Coiflets, Symlets, Fejér-Korovkin, Дискретный Мейер, Биоортогональный, и Противоположный Биоортогональный. Смотрите wfilters для вейвлетов, доступных в каждом семействе.

Пример: 'db4'

Масштабирование (lowpass) фильтр, заданный как ровная длина вектор с действительным знаком. LoD должен быть той же длиной как HiD. Смотрите wfilters для деталей.

Типы данных: double

Вейвлет (highpass) фильтр, заданный как ровная длина вектор с действительным знаком. HiD должен быть той же длиной как LoD. Смотрите wfilters для деталей.

Типы данных: double

Дополнительный режим, используемый при выполнении DWT, заданного как одно из следующего:

mode

Режим расширения DWT

'zpd'

Дополнение нулями

'sp0'

Сглаживайте расширение порядка 0

'spd' (or 'sp1')

Сглаживайте расширение порядка 1

'sym' или 'symh'

Симметричное расширение (половина точки): граничное значение симметричная репликация

'symw'

Симметричное расширение (самое главное): граничное значение симметричная репликация

'asym' или 'asymh'

Антисимметричное расширение (половина точки): граничное значение антисимметричная репликация

'asymw'

Антисимметричное расширение (самое главное): граничное значение антисимметричная репликация

'ppd'

Расширение Periodized (1)

'per'

Расширение Periodized (2)

Если длина сигнала нечетна, wextend добавляет направо дополнительную выборку, которая равна последнему значению и выполняет расширение с помощью режима 'ppd'. В противном случае 'per' уменьшает до 'ppd'. Это правило также применяется к изображениям.

Глобальная переменная, управляемая dwtmode, задает режим расширения по умолчанию. Смотрите dwtmode для дополнительных описаний режима.

Пример: [cA,cD] = dwt(x,'db4','mode','symw') возвращает одноуровневый DWT x с помощью порядка 4 Daubechies экстремальный вейвлет фазы и самое главное симметричное расширение.

Выходные аргументы

свернуть все

Коэффициенты приближения получены из разложения вейвлета, возвращенного как вектор. При свертке к входному сигналу x с масштабирующимся фильтром LoD, сопровождаемый двухместным десятикратным уменьшением, приводит к коэффициентам приближения. Позвольте sx = size(x) и lf = длина фильтров разложения.

  • Если дополнительный режим DWT установлен в periodization, cA является вектором длины ceil(sx/2).

  • Для других дополнительных режимов cA является вектором длины floor((sx+lf-1)/2).

Типы данных: double

Детализируйте коэффициенты, полученные из разложения вейвлета, возвращенного как вектор. Свертка к входному сигналу, x с вейвлетом фильтрует HiD, сопровождаемый двухместным десятикратным уменьшением, приводит к коэффициентам детали. Позвольте sx = size(x) и lf = длина фильтров разложения.

  • Если дополнительный режим DWT установлен в periodization, cD является вектором длины ceil(sx/2).

  • Для других дополнительных режимов cD является вектором длины floor((sx+lf-1)/2).

Типы данных: double

Алгоритмы

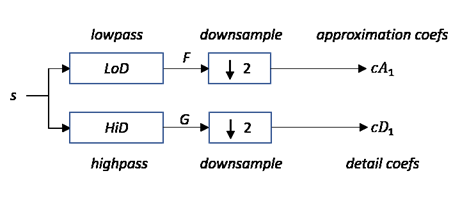
При запуске с s сигнала длины N вычисляются два набора коэффициентов: коэффициенты приближения cA 1 и коэффициенты детали cD 1. При свертке к s с масштабирующимся фильтром LoD, сопровождаемый двухместным десятикратным уменьшением, приводит к коэффициентам приближения. Точно так же применяющий операцию свертки s с HiD фильтра вейвлета, сопровождаемым двухместным десятикратным уменьшением, приводит к коэффициентам детали.

где

  • — Примените операцию свертки с фильтром X

  • ↓2 — Субдискретизируйте (сохраните даже индексированные элементы),

Длина каждого фильтра равна 2n. Если N = длина (s), сигналы, F и G имеют длину N + 2n −1 и коэффициенты cA 1 и cD 1, имеет пол длины(N−12)+n.

Чтобы иметь дело с эффектами конца сигнала, следующими из основанного на свертке алгоритма, глобальная переменная, управляемая dwtmode, задает вид дополнительного используемого режима сигнала. Возможные варианты включают дополняющее нуль и симметричное расширение, которое является режимом по умолчанию.

Примечание

Для того же входа эта функция dwt и блок DWT в DSP System Toolbox™ не приводят к тем же результатам. Блок DWT разработан для реализации в реальном времени, в то время как программное обеспечение Wavelet Toolbox™ разработано для анализа, таким образом, продукты обрабатывают граничные условия и фильтруют состояния по-другому.

Чтобы сделать функцию dwt выходным соответствием блок DWT вывод, установите функциональное граничное условие к дополнению нуля путем ввода dwtmode('zpd') в командной строке MATLAB®. Чтобы совпадать с задержкой блока DWT, который реализован с помощью КИХ-фильтров, добавляют, нули к входу функции dwt. Количество нулей, которые вы добавляете, должно быть равно половине длины фильтра.

Ссылки

[1] Daubechies, я. Десять лекций по вейвлетам. CBMS-NSF региональный ряд конференции в прикладной математике. Филадельфия, PA: общество промышленной и прикладной математики, 1992.

[2] Mallat, S. G. “Теория для Разложения Сигнала Мультиразрешения: Представление Вейвлета”. Транзакции IEEE согласно Анализу Шаблона и Искусственному интеллекту. Издание 11, Выпуск 7, июль 1989, стр 674–693.

[3] Мейер, Y. Вейвлеты и операторы. Переведенный Д. Х. Сэлинджером. Кембридж, Великобритания: Издательство Кембриджского университета, 1995.

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Смотрите также

| | | |

Представлено до R2006a

Документация Wavelet Toolbox
Поддержка