Exponenta Banner

dwtleader

Мультифрактальные 1D оценки лидера вейвлета

свернуть все на странице

Синтаксис

[dh,h] = dwtleader(x)
[dh,h,cp] = dwtleader(x)
[dh,h,cp,tauq] = dwtleader(x)
[dh,h,cp,tauq,leaders] = dwtleader(___)
[dh,h,cp,tauq,leaders,structfunc] = dwtleader(___)
[___]= dwtleader(x,wname)
[___] = dwtleader(___,Name,Value)

Описание

пример

[dh,h] = dwtleader(x) возвращает спектр особенности, dh, и экспоненты Держателя, h, для 1D данных с действительным знаком, x. Спектр особенности и экспоненты Держателя оцениваются в течение линейно распределенных моментов функций структуры от –5 до +5.

пример

[dh,h,cp] = dwtleader(x) также возвращает первые три журнала cumulants, cp масштабирующихся экспонент.

пример

[dh,h,cp,tauq] = dwtleader(x) также возвращает масштабирующиеся экспоненты в течение линейно расположенных с интервалами моментов от –5 до 5. Лидеры вейвлета не заданы для самой прекрасной шкалы.

[dh,h,cp,tauq,leaders] = dwtleader(___) также возвращает лидеров вейвлета шкалой.

[dh,h,cp,tauq,leaders,structfunc] = dwtleader(___) также возвращает функции структуры мультиразрешения.

[___]= dwtleader(x,wname) использует ортогональный или биоортогональный вейвлет, заданный wname, чтобы вычислить лидеров вейвлета и фрактальные оценки.

[___] = dwtleader(___,Name,Value) возвращает лидеров вейвлета и другие заданные выходные параметры с дополнительными опциями, заданными одним или несколькими аргументами пары Name,Value.

Примеры

свернуть все

Скрипт Open Live Script

Сравните мультифрактальный спектр данных об изменчивости сердечного ритма до и после применения препарата, который уменьшает сердечную динамику.

load hrvDrug;
predrug = hrvDrug(1:4642);
postdrug = hrvDrug(4643:end);
[dhpre,hpre] = dwtleader(predrug);
[dhpost,hpost] = dwtleader(postdrug);
plot(hpre,dhpre,hpost,dhpost)
xlabel('h')
ylabel('D(h)')
grid on
legend('Predrug','Postdrug')

Распространение значений экспоненты Держателя перед введением лекарства (приблизительно 0,08 к 0,55) намного больше, чем распространение значений позже (приблизительно 0,08 к 0,31). Это указывает, что сердечный ритм стал большим количеством монофрактала.

Скрипт Open Live Script

Вычислите спектр особенности и cumulants для Броуновского шумового процесса.

Создайте Броуновский шумовой сигнал.

rng(100);
x = cumsum(randn(2^15,1));

Получите и постройте спектр особенности.

[dh,h,cp] = dwtleader(x);
plot(h,dh,'o-','MarkerFaceColor','b') 
grid on
title({'Singularity Spectrum'; ['First Cumulant ' num2str(cp(1))]})

Маленькое распространение в экспонентах Держателя (приблизительно 0,472 к 0,512) указывает, что этот Броуновский шумовой сигнал может быть охарактеризован глобальной экспонентой Держателя 0,49875. Теоретическая экспонента Держателя для Броуновского движения 0.5.

Получите cumulants.

cp
cp = 1×3

    0.4554   -0.0121   -0.0000

Первое cumulant значение является наклоном масштабирующихся экспонент по сравнению с моментами. Вторые и третьи cumulants указывают на отклонение от линейности. Первое cumulant значение и почти нулевые значения второго и третьего cumulants указывают, что масштабирующиеся экспоненты являются линейной функцией моментов. Поэтому этот сигнал Броуновского движения является монофракталом.

Скрипт Open Live Script

Вычислите cumulants для мультифрактального случайного обхода. Мультифрактальный случайный обход является реализацией вероятностного процесса с теоретическим первым cumulant 0,75 и вторым cumulant –0.05. Второе cumulant значение –0.05 указывает, что масштабирующиеся экспоненты отклоняются от линейной функции с наклоном 0.75.

Загрузите случайный сигнал обхода. 

load mrw07505

Получите и отобразите первый и второй cumulants.

[~,~,cp,tauq] = dwtleader(mrw07505);
cp([1 2])
ans = 1×2

    0.7504   -0.0554

Для монофрактальных процессов масштабирующиеся экспоненты являются линейной функцией моментов. Линейность обозначается вторым и третьим cumulants, являющимся близко к нулю. В этом случае ненулевой второй cumulant указывает, что процесс является мультифракталом.

Постройте масштабирующиеся экспоненты для q th моменты.

plot(-5:5,tauq,'bo--')
title('Estimated Scaling Exponents')
grid on
xlabel('qth Moments')
ylabel('\tau(q)')

Масштабирующиеся экспоненты являются нелинейной функцией моментов.

Входные параметры

свернуть все

Входной сигнал, заданный как 1D вектор действительных значений. Для вейвлета по умолчанию и минимального уровня регрессии, временные ряды должны иметь по крайней мере 248 выборок. Для значений не по умолчанию требуемая от минимума длина данных зависит от фильтра вейвлета и уровней, используемых в модели регрессии. Метод лидеров вейвлета работает лучше всего на данные с 8000 или больше выборок.

Имя вейвлета, заданное как вектор символов или скаляр строки. wname является кратким названием семейства вейвлетов и номером фильтра, распознанным менеджером по вейвлету, wavemngr.

Чтобы запросить допустимые краткие названия семейства вейвлетов, используйте wavemngr('read'). Чтобы определить, является ли конкретный вейвлет ортогональным или биоортогональным, используйте waveinfo с кратким названием семейства вейвлетов, например, waveinfo('db'). Также используйте wavemngr с опцией 'type', например, wavemngr('type','fk4'). Возвращенное значение 1 указывает на ортогональный вейвлет. Возвращенное значение 2 указывает на биоортогональный вейвлет.

Аргументы в виде пар имя-значение

Укажите необязательные аргументы в виде пар ""имя, значение"", разделенных запятыми. Имя (Name) — это имя аргумента, а значение (Value) — соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: 'MinRegressionLevel',5 устанавливает минимальный уровень регрессии на 5.

Опция веса, чтобы использовать в модели регрессии метода взвешенных наименьших квадратов, чтобы определить спектр особенности, экспоненты Держателя, cumulants, и масштабирующиеся экспоненты, заданные как пара, разделенная запятой, состоящая из 'RegressionWeight' и или 'uniform' или 'scale'. Опция 'uniform' применяет равный вес к каждой шкале. Опция 'scale' использует количество лидеров вейвлета шкалой как веса.

Примечание

Чтобы копировать поведение dwtleader, найденного в релизах до R2018a, обновите все экземпляры dwtleader, чтобы включать набор аргумента пары "имя-значение" 'RegressionWeight' в 'scale'.

Минимальный уровень регрессии, minlev, заданный как пара, разделенная запятой, состоящая из 'MinRegressionLevel' и положительного целого числа, больше, чем или равный 2. Только уровни, больше, чем или равный заданному минимальному уровню, используются в мультифрактальных оценках. dwtleader требует, чтобы по крайней мере 6 лидеров вейвлета в максимальном уровне и два уровня использовались в мультифрактальных оценках. Шкала в дискретном вейвлете преобразовывает соответствие минимальному уровню, twominlev. Чем более сглаженны данные (то есть, ближе экспоненты Держателя к 1), тем менее вероятно, что сокращение минимального уровня регрессии ухудшит результаты.

Максимальный уровень регрессии, maxlev, заданный как положительное целое число, больше, чем или равный minlev + 1. Максимальный уровень использует только уровни, меньше чем или равные maxlev в мультифрактальных оценках. Шкала в дискретном вейвлете преобразовывает соответствие максимальному уровню, 2maxlev. Задайте максимальный уровень регрессии когда это необходимо, чтобы ограничить уровни, используемые в регрессии к значению меньше, чем уровень по умолчанию. Чтобы определить количество лидеров вейвлета уровнем, используйте выходной аргумент leaders или поле weights выходного аргумента structfunc. Значение по умолчанию является самым большим уровнем по крайней мере с шестью лидерами вейвлета

Выходные аргументы

свернуть все

Спектр особенности, возвращенный как вектор. Спектр особенности оценивается использование функций структуры, определенных в течение линейно распределенных моментов от –5 до 5. Функции структуры вычисляются на основе лидеров вейвлета, полученных с помощью биоортогонального фильтра вейвлета сплайна. Биоортогональный фильтр вейвлета сплайна, который используется, имеет один исчезающий момент в вейвлете синтеза и пять исчезающих моментов в аналитическом вейвлете ('bior1.5'). По умолчанию мультифрактальные оценки выведены от лидеров вейвлета в минимальном уровне 3 и максимальный уровень, где существует по крайней мере шесть лидеров вейвлета.

Оценки экспоненты держателя, возвращенные как вектор 1 на 11 скаляров. Экспоненты держателя характеризуют регулярность сигнала. Чем ближе экспонента Держателя к 1, тем ближе функция к дифференцируемому. С другой стороны, чем ближе экспонента Держателя должна обнулить, тем ближе функция к прерывистому.

Типы данных: double

Cumulants, возвращенный как 1 3 вектор скаляров. Вектор содержит первые три журнала cumulants масштабирующихся экспонент. Первый cumulant характеризует линейное поведение в масштабирующихся экспонентах. Вторые и третьи cumulants характеризуют отклонение от линейности.

Типы данных: double

Масштабирование экспонент, возвращенных как вектор-столбец. Экспоненты в течение линейно распределенных моментов от –5 до +5.

leaders является массивом ячеек с i th элемент, содержащий лидеров вейвлета на уровне i +1 или шкала 2 (i +1). Лидеры вейвлета не заданы на уровне 1.

Структура мультиразрешения функционирует для глобальных оценок экспоненты Держателя, возвращенных как struct. Функция структуры для данных x задана как

S(q,a)=1na∑k=1na|Tx(a,k)|q≃aζ(q),

где a является шкалой, q является моментом, Tx лидеры вейвлета шкалой, na является количеством лидеров вейвлета в каждой шкале, и ζ(q) масштабирующаяся экспонента. Расширение ζ(q) к полиному производит

ζ(q)=c1q+c2q2/2+c3q3/6+...

Масштабирующиеся экспоненты могут быть оценены от журнала-cumulants коэффициентов лидера вейвлета. Когда ζ(q) линейная функция, сигнал является монофракталом. Когда это отклоняется от линейного, сигнал является мультифракталом.

structfunc является массивом структур, содержащим следующие поля:

  • Tq — Измерения входа, x, в различных шкалах. Tq является матрицей количеств мультиразрешения, которые зависят совместно вовремя и шкала. Масштабирующиеся явления в x подразумевают отношение закона степени между моментами Tq и шкалы. Для dwtleader полем Tq является Ns-by-36 матрица, где Ns является количеством шкал, используемых в мультифрактальных оценках. Первые 11 столбцов Tq являются масштабирующимися оценками экспоненты шкалы для каждого q th моменты от –5 до 5. Следующие 11 столбцов содержат оценки спектра особенности, dh, для каждого q th моменты. Столбцы 23-33 содержат оценки экспоненты Держателя, h. Последние три столбца содержат оценки для первого порядка, второго порядка, и третий порядок cumulants, соответственно.

  • weights — Веса используются в регрессии. Веса являются количеством лидеров вейвлета шкалой. weights является Ns-by-1 вектор.

  • logscales — Шкалы, используемые в качестве предикторов в регрессии. logscales является Ns-by-1 вектор с основой 2 логарифма шкал.

Алгоритмы

Лидеры вейвлета выведены от критически выбранных коэффициентов дискретного вейвлета преобразовывает (DWT). Лидеры вейвлета предлагают значительные теоретические преимущества перед коэффициентами вейвлета в мультифрактальном формализме. Лидеры вейвлета время - или локализованная пробелом супрема абсолютного значения дискретных коэффициентов вейвлета. Локализация времени супремы требует, чтобы коэффициенты вейвлета были получены с помощью сжато поддерживаемого вейвлета. Экспоненты Держателя, которые определяют количество локальной регулярности, определяются от них супрема. Спектр особенности указывает на размер набора экспонент Держателя в данных.

1D лидеры вейвлета заданы как

Lx(j,k)=глотокλ'⊂3λj,k|dx(j,k)|

где шкалы 2j, переведены в положения времени 2jk. Окружение времени 3λj,k=λj,k−1∪λj,k∪λj,k+1, где λj,k=[k2j,(k+1)2j). Окружение времени взято по шкале и всем более прекрасным шкалам. dx(j,k) является коэффициентами вейвлета.

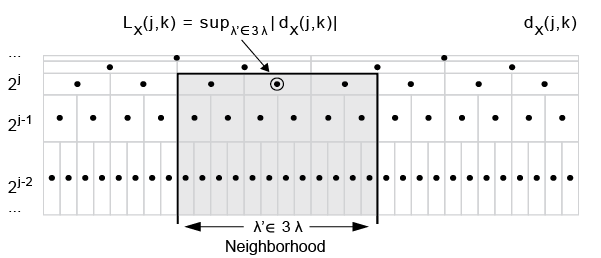
Вычислить лидеров вейвлета, Lx(j,k):

  1. Вычислите коэффициенты вейвлета, dx(j,k), использование дискретного вейвлета преобразовывает и сохраняет абсолютное значение каждого коэффициента для каждой шкалы. Каждая более прекрасная шкала имеет дважды количество коэффициентов, чем следующая более грубая шкала. Каждый двухместный интервал в шкале 2j может быть записан как объединение двух интервалов в более прекрасной шкале.

    [2jk,2j(k+1))=[2j−1(2k),2j−1(2k+2))[2j−1(2k),2j−1(2k+2))=[2j−1(2k),2j−1(2k+1))∪[2j−1(2k+1),2j−1(2k+2))

  2. Запустите в шкале, которая является одним уровнем, более грубым, чем самая прекрасная полученная шкала.

  3. Сравните первое значение со всеми его более прекрасными двухместными интервалами и получите максимальное значение.

  4. Перейдите к следующему значению и сравните его значение со всеми его более прекрасными значениями шкалы.

  5. Продолжите сравнивать значения с их вложенными значениями и получать максимумы.

  6. От максимальных значений, полученных для той шкалы, исследуйте первые три значения и получите максимум тех соседей. То максимальное значение является лидером для той шкалы.

  7. Продолжите сравнивать максимальные значения, чтобы получить других лидеров для той шкалы.

  8. Переместитесь в следующую более грубую шкалу и повторите процесс.

Например, примите, что у вас есть эти абсолютные значения коэффициентов в этих шкалах:

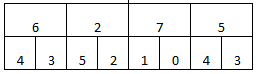
Начиная с верхней строки, которая является следующим самым грубым уровнем от самой прекрасной шкалы (нижний ряд), сравнивают каждое значение с его двухместными интервалами и получают максимумы.

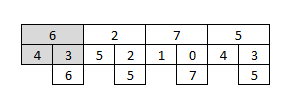
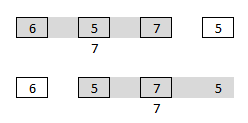
Затем посмотрите на три соседних значения и получите максимум. Повторитесь для следующих трех соседей. Эти максимумы, 7 и 7, являются лидерами вейвлета для этого уровня.

Ссылки

[1] Вендт, H. и П. Абри. "Тесты Multifractality Используя Загруженных Лидеров Вейвлета". Транзакции IEEE на Обработке сигналов. Издание 55, № 10, 2007, стр 4811–4820.

[2] Jaffard, S., Б. Лэшермес и П. Абри. “Лидеры вейвлета в Мультифрактальном Анализе”. Анализ вейвлета и Приложения. Т. Цянь, М. Ай. Вай, и С. Юэшэн, Редакторы 2006, стр 219–264.

Смотрите также

|

Темы

Введенный в R2017b

Документация Wavelet Toolbox
Поддержка