Управление "линейным квадратичным гауссовым" (LQG) является современным методом пространства состояний для разработки оптимальных динамических регуляторов и диспетчеров сервомотора с интегральным действием (также известный как средства отслеживания заданного значения). Этот метод позволяет вам обменивать производительность регулирования/средства отслеживания и усилие по управлению, и учитывать воздействия процесса и шум измерения.
Чтобы спроектировать регуляторы LQG и средства отслеживания заданного значения, вы выполняете следующие шаги:
Создайте оптимальное LQ усиление.
Создайте Фильтр Калмана (средство оценки состояния).
Сформируйте проект LQG путем соединения оптимального LQ усиления и Фильтра Калмана.
Для получения дополнительной информации об использовании проекта LQG, чтобы создать регуляторы LQG, см. Проект "линейного квадратичного гауссова" (LQG) для Регулирования.
Для получения дополнительной информации об использовании проекта LQG, чтобы создать контроллеры сервомотора LQG, см. Проект "линейного квадратичного гауссова" (LQG) Контроллера Сервомотора с Интегральным Действием.
Эти темы фокусируются на случае непрерывного времени. Для получения информации о дискретном времени проект LQG смотрите dlqr и kalman страницы с описанием.
Можно спроектировать регулятор LQG, чтобы отрегулировать выход y вокруг нуля в следующей модели.
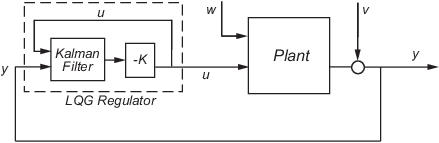
Объект в этой модели испытывает воздействия (шум процесса) w и управляется средствами управления u. Регулятор использует шумные измерения y, чтобы сгенерировать эти средства управления. Состояние объекта и уравнения измерения принимают форму
и и w и v моделируются как белый шум.
Проект LQG требует модели в пространстве состояний объекта. Можно использовать ss преобразовывать другие форматы модели в пространство состояний.
Чтобы спроектировать регуляторы LQG, можно использовать методы проектирования, показанные в следующей таблице.
| Спроектировать регулятор LQG, использующий... | Используйте следующие команды: |
|---|---|
|
Быстрый, метод проектирования с одним шагом, когда следующее верно:
| lqg |
|
Более гибкий, метод проектирования с тремя шагами, который позволяет вам задавать:
|
Для получения дополнительной информации смотрите
|
Вы создаете оптимальное LQ усиление из следующих элементов:
Чтобы создать оптимальное усиление, введите следующую команду:
K= lqr(A,B,Q,R,N)
Эта команда вычисляет оптимальную матрицу усиления K, для которого закон об обратной связи состояния минимизирует следующую квадратичную функцию стоимости в течение непрерывного времени:
Программное обеспечение вычисляет матрицу усиления K путем решения алгебраического уравнения Riccati.
Для получения информации о построении оптимального LQ усиления, включая функцию стоимости, которую программное обеспечение минимизирует в течение дискретного времени, смотрите lqr страница с описанием.
Вам нужно средство оценки состояния Кальмана для регулирования LQG и сервоуправления, потому что вы не можете реализовать оптимальную оптимальную LQ обратную связь состояния без полного измерения состояния.
Вы создаете оценку состояния таким образом, что остается оптимальным для проблемы выходной обратной связи. Вы создаете усиление средства оценки состояния Кальмана из следующих элементов:
Вы создаете средство оценки состояния Кальмана таким же образом и для регулирования и для сервоуправления.
Чтобы создать средство оценки состояния Кальмана, введите следующую команду:
[kest,L,P] = kalman(sys,Qn,Rn,Nn);
Эта команда вычисляет средство оценки состояния Кальмана, kest следующими уравнениями объекта:
где w и v моделируются как белый шум. L усиление Кальмана и P ковариационная матрица.
Программное обеспечение генерирует эту оценку состояния с помощью Фильтра Калмана
с входными параметрами u (средства управления) и y (измерения). Шумовые данные о ковариации
решает, что Кальман получает L посредством алгебраического уравнения Riccati.
Фильтр Калмана является оптимальным средством оценки при контакте с Гауссовым белым шумом. А именно, это минимизирует асимптотическую ковариацию
из ошибки оценки .
![]()
Для получения дополнительной информации смотрите kalman страница с описанием. Для полного примера реализации Фильтра Калмана смотрите Кальмана Филтеринга.
Чтобы сформировать регулятор LQG, соедините Фильтр Калмана kest и оптимальное LQ усиление K путем ввода следующей команды:
regulator = lqgreg(kest, K);
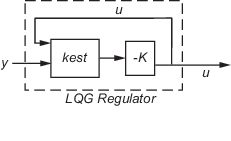
У регулятора есть следующие уравнения пространства состояний:
Для получения дополнительной информации о формировании регуляторов LQG смотрите lqgreg и регулирование LQG: тематическое исследование металлопрокатного завода.
Можно спроектировать контроллер сервомотора с интегральным действием для следующей модели:
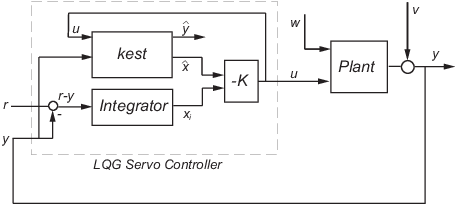
Контроллер сервомотора, который вы проектируете, гарантирует, что выход y отслеживает ссылочную команду r при отклонении воздействий процесса w и шум измерения v.
Объект в предыдущей фигуре подвергается воздействиям w и управляется средствами управления u. Контроллер сервомотора использует шумные измерения y, чтобы сгенерировать эти средства управления. Состояние объекта и уравнения измерения имеют форму
и и w и v моделируются как белый шум.
Проект LQG требует модели в пространстве состояний объекта. Можно использовать ss преобразовывать другие форматы модели в пространство состояний.
Чтобы спроектировать контроллеры сервомотора LQG, можно использовать методы проектирования, показанные в следующей таблице.
| Спроектировать контроллер сервомотора LQG, использующий... | Используйте следующие команды: |
|---|---|
|
Быстрый, метод проектирования с одним шагом, когда следующее верно:
| lqg |
|
Более гибкий, метод проектирования с тремя шагами, который позволяет вам задавать:
|
Для получения дополнительной информации смотрите
|
Вы создаете оптимальное LQ усиление из
Модель объекта управления пространства состояний sys
Взвешивание матриц QR, и N, которые задают компромисс между производительностью средства отслеживания и управляют усилием
Чтобы создать оптимальное усиление, введите следующую команду:
K= lqi(sys,Q,R,N)
Эта команда вычисляет оптимальную матрицу усиления K, для которого закон об обратной связи состояния минимизирует следующую квадратичную функцию стоимости в течение непрерывного времени:
Программное обеспечение вычисляет матрицу усиления K путем решения алгебраического уравнения Riccati.
Для получения информации о построении оптимального LQ усиления, включая функцию стоимости, которую программное обеспечение минимизирует в течение дискретного времени, смотрите lqi страница с описанием.
Вам нужно средство оценки состояния Кальмана для регулирования LQG и сервоуправления, потому что вы не можете реализовать оптимальную LQ обратную связь состояния без полного измерения состояния.
Вы создаете оценку состояния таким образом, что остается оптимальным для проблемы выходной обратной связи. Вы создаете усиление средства оценки состояния Кальмана из следующих элементов:
Вы создаете средство оценки состояния Кальмана таким же образом и для регулирования и для сервоуправления.
Чтобы создать средство оценки состояния Кальмана, введите следующую команду:
[kest,L,P] = kalman(sys,Qn,Rn,Nn);
Эта команда вычисляет средство оценки состояния Кальмана, kest следующими уравнениями объекта:
где w и v моделируются как белый шум. L усиление Кальмана и P ковариационная матрица.
Программное обеспечение генерирует эту оценку состояния с помощью Фильтра Калмана
с входными параметрами u (средства управления) и y (измерения). Шумовые данные о ковариации
решает, что Кальман получает L посредством алгебраического уравнения Riccati.
Фильтр Калмана является оптимальным средством оценки при контакте с Гауссовым белым шумом. А именно, это минимизирует асимптотическую ковариацию
из ошибки оценки .
![]()
Для получения дополнительной информации смотрите kalman страница с описанием. Для полного примера реализации Фильтра Калмана смотрите Кальмана Филтеринга.
Чтобы сформировать две степени свободы контроллер сервомотора LQG, соедините Фильтр Калмана kest и оптимальное LQ усиление K путем ввода следующей команды:
servocontroller = lqgtrack(kest, K);
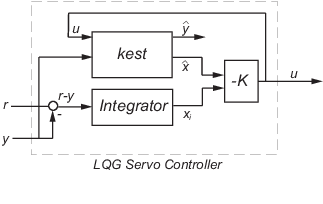
У контроллера сервомотора есть следующие уравнения пространства состояний:
Для получения дополнительной информации о формировании контроллеров сервомотора LQG, включая то, как сформировать одну степень свободы контроллер сервомотора LQG, смотрите lqgtrack страница с описанием.
kalman | lqg | lqgreg | lqgtrack | lqi | lqr