Минимизация со связанными ограничениями и полосным предварительным формирователем

Цель в этой проблеме состоит в том, чтобы минимизировать нелинейную функцию

$f (x) = 1 + \sum_{i = 1}^{n} {| (3 - 2 x_{i}) x_{i} - x_{i - 1} - x_{i + 1} + 1 |}^{p} + \sum_{i = 1}^{n / 2} {| x_{i} + x_{i + n / 2} |}^{p},$

таким образом, что-10.0 ≤ _xi ≤ 10.0, где n 800 (n должен быть кратным 4), p = 7/3, и x ₀ = x _n + 1 = 0.

Шаг 1: Запишите файл tbroyfg.m, который вычисляет целевую функцию и градиент цели

tbroyfg.m файл вычисляет значение функции и градиент. Этот файл длинен и не включен здесь. Вы видите код для этой функции с помощью команды

type tbroyfg

Шаблон разреженности матрицы Гессиана был предопределен и сохранен в файле tbroyhstr.mat. Структура разреженности для Гессиана этой проблемы соединена, как вы видите в следующем spy график.

load tbroyhstr
spy(Hstr)

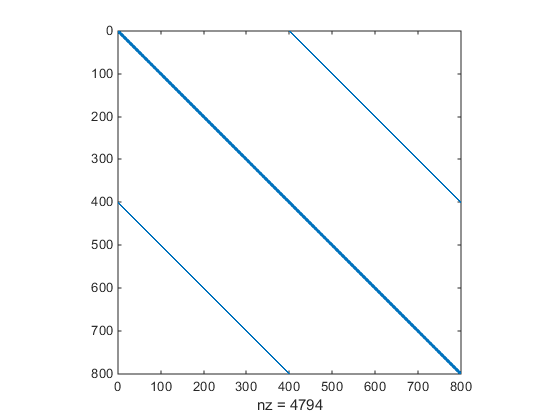
В этом графике центральная дорожка является самостоятельно пятью ленточными матрицами. Следующий график показывает матрицу более ясно:

spy(Hstr(1:20,1:20))

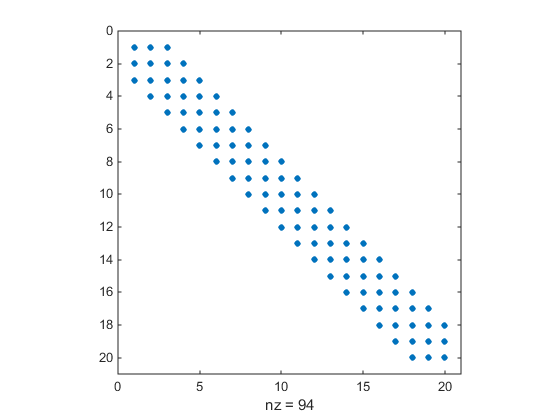
Используйте optimoptions установить HessPattern параметр к Hstr. Когда проблема, столь большая, как это имеет очевидную структуру разреженности, не устанавливая HessPattern параметр требует огромной суммы ненужной памяти и расчета. Это вызвано тем, что fmincon попытки использовать конечное дифференцирование на полной матрице Гессиана 640 000 ненулевых записей.

Необходимо также установить SpecifyObjectiveGradient параметр к true использование optimoptions, поскольку градиент вычисляется в tbroyfg.m. Затем выполните fmincon как показано на Шаге 2.

Шаг 2: Вызовите нелинейную стандартную программу минимизации с начальной точкой xstart.

fun = @tbroyfg;
load tbroyhstr          % Get Hstr, structure of the Hessian
n = 800;
xstart = -ones(n,1); xstart(2:2:n) = 1;
lb = -10*ones(n,1); ub = -lb;
options = optimoptions('fmincon','SpecifyObjectiveGradient',true,'HessPattern',Hstr,...
    'Algorithm','trust-region-reflective'); 

[x,fval,exitflag,output] = ... 
   fmincon(fun,xstart,[],[],[],[],lb,ub,[],options);

exitflagfval , мера по оптимальности первого порядка (output.firstorderopt), и количество итераций (output.iterations):

exitflag,fval,output.firstorderopt,output.iterations
exitflag =

     3


fval =

  270.4790


ans =

    0.0163


ans =

     7

Для связанных ограниченных проблем оптимальность первого порядка является нормой по бесконечности v.*g, где v задан как в Ограничениях Поля и g градиент.

Из-за центральной дорожки с пятью полосами можно улучшить решение при помощи предварительного формирователя с пятью полосами вместо диагонального предварительного формирователя по умолчанию. Используя optimoptions функция, сброс PrecondBandWidth параметр к 2 и решите задачу снова. (Пропускная способность является количеством верхних (или ниже) диагонали, не считая основную диагональ.)

fun = @tbroyfg;
load tbroyhstr          % Get Hstr, structure of the Hessian
n = 800;
xstart = -ones(n,1); xstart(2:2:n,1) = 1;
lb = -10*ones(n,1); ub = -lb;
options = optimoptions('fmincon','SpecifyObjectiveGradient',true,'HessPattern',Hstr, ...
    'Algorithm','trust-region-reflective','PrecondBandWidth',2);

[x,fval,exitflag,output] = ...
   fmincon(fun,xstart,[],[],[],[],lb,ub,[],options);

Количество итераций увеличивается на два. Но мера по оптимальности первого порядка уменьшается фактором 1e-3:

exitflag,fval,output.firstorderopt,output.iterations
exitflag =

     3


fval =

  270.4790


ans =

   7.5340e-05


ans =

     9

Документация