Эта тема обращается к программному обеспечению Simscape™ Multibody™ First Generation. Библиотека первого поколения будет скоро удержана от использования. Чтобы избежать проблем совместимости, создайте любые новые модели и преобразуйте любые существующие модели с помощью блоков второго поколения — доступные путем ввода команды smlib в командной строке MATLAB®.
Платформа Стюарта является классическим проектом для управления положением и движением, первоначально предложенного в 1 965 как средство моделирования рейса, и все еще обычно используемый с этой целью [1]. С тех пор широкий спектр приложений извлек выгоду из платформы Стюарта. Несколько отраслей промышленности с помощью этого проекта включают космос, автомобильную, навигационную технологию, и устройства. Платформа использовалась, чтобы симулировать рейс, смоделировать лунный марсоход, навести мосты, помощь в обслуживании транспортного средства, механизмах подъема подъемного крана проекта, и тарелках спутниковой связи положения и телескопах, среди других задач.
Платформа Стюарта имеет исключительную область значений движения и может быть точно и легко расположена и ориентирована. Платформа обеспечивает большую сумму жесткости или жесткость, для данной структурной массы, и таким образом обеспечивает значительную позиционную уверенность. Модель платформы является умеренно комплексной с большим количеством механических ограничений, которые требуют устойчивой симуляции.
Большинство вариантов платформы Стюарта имеет шесть линейно приводимых в движение участков с различными комбинациями связей платформы участка. Полный блок является параллельным механизмом, состоящим из твердого тела главная или мобильная пластина, соединенная с неподвижной опорной плитой и заданная по крайней мере тремя стационарными точками на заземленной базе, соединенной с участками.
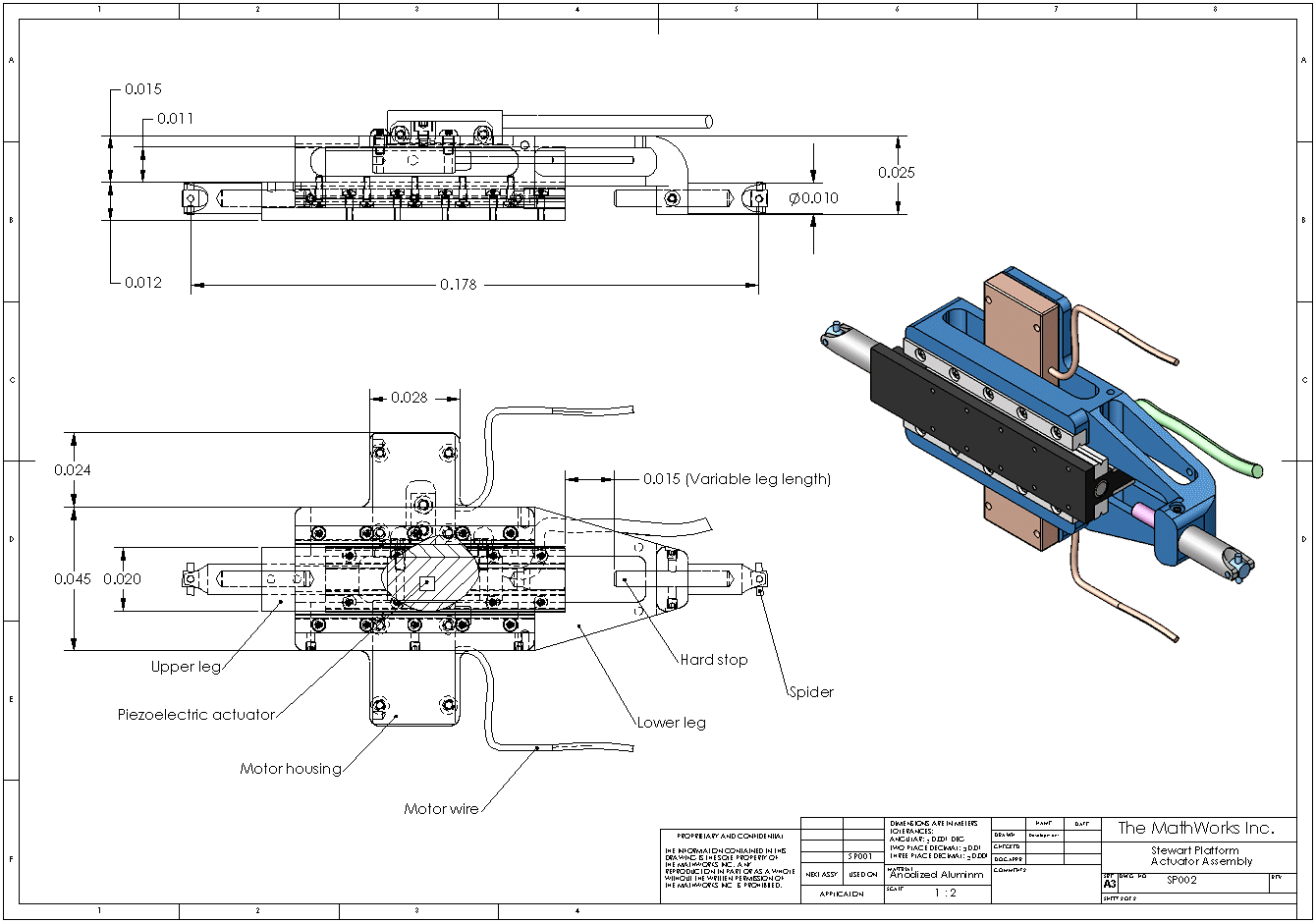
Платформа Стюарта, используемая здесь, соединяется с опорной плитой в шести точках универсальными соединениями. Каждый участок имеет две части, верхнее и более низкое, соединенный цилиндрическим соединением. Каждое бедро соединяется с главной пластиной другим универсальным соединением. Таким образом платформа имеет 6*2 + 1 = 13 мобильных частей и 6*3 = 18 соединений, соединяющих части.
Стюарт Плэтформ
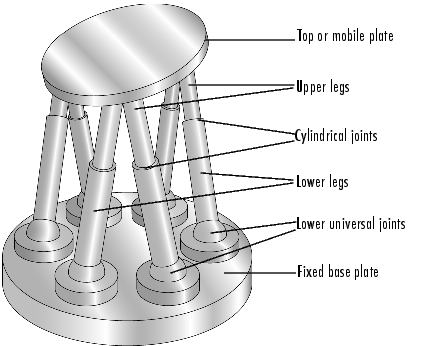
Следующий рисунок показывает подробную схематическую из платформы Стюарта.
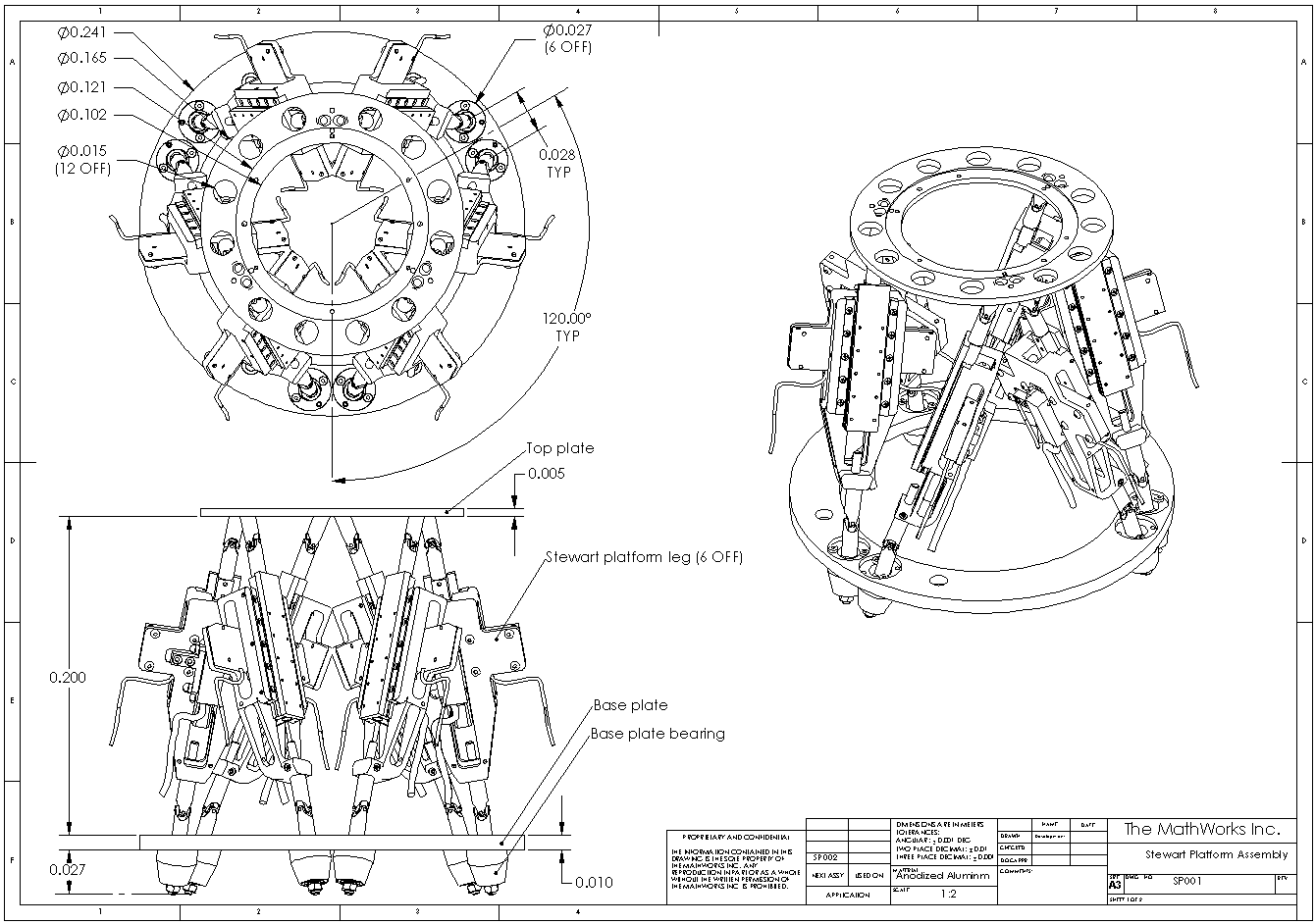
Следующий рисунок показывает подробный схематический из одного участка платформы Стюарта.
Стандарт проект платформы Стюарта имеет шесть независимых степеней свободы (число степеней свободы). Мобильная пластина, если отключено от участков и таким образом неограниченный, также имеет шесть чисел степеней свободы. Платформа Стюарта поэтому точно воспроизводит возможное движение свободной пластины, но с дополнительным преимуществом устойчивого и точного управления расположением.
Вот два способа считать число степеней свободы платформы Стюарта.
Подсчет Степеней свободы на Телах на Пробеле запускается с демонтированных частей платформы как физические тела на пробеле.
Подсчет Степеней свободы как Объединенные Примитивы запускается с платформы, представленной как соединенное Тело и Блоки соединений.
Запустите с демонтированных частей платформы Стюарта как неограниченные движущиеся контактирующие тела. Когда вы собираете платформу, вы ограничиваете тела, когда вы соединяете их с соединениями. Опорная плита неподвижна.
Этот подход состоит не то, как в том, что симуляция Simscape Multibody считает число степеней свободы. Смотрите Степени свободы подсчета как Объединенные Примитивы.
Тела с числом степеней свободы. Каждое свободное тело на пробеле имеет шесть чисел степеней свободы. Только после того, как вы присоединяете их друг к другу с соединениями, они более не способный переместиться свободно.
Соединения как Ограничения. Соединение тел с соединениями ограничивает эти два тела, таким образом, они больше не могут перемещаться свободно друг относительно друга.
Например, универсальная объединенная связь позволяет две вращательных степени свободы, но налагает четыре ограничения, три (позиционных) поступательных и одно вращательное.
Сборка Частей Платформы Стюарта. Начните собирать платформу Стюарта. Каждое объединенное прикрепление одновременно соединяет и ограничивает тела. В целом, каждый участок налагает 12 ограничений на себя и главную пластину.
universals соединение голеней к опорной плите налагают четыре ограничения:
Три позиционных, требуя, чтобы были расположены две точки
Одно вращательное, препятствуя тому, чтобы голень вращалась о ее продольной оси (относительно неподвижной основы)
cylindricals соединение верхнего к голеням налагают четыре ограничения:
Два позиционных, позволяя этим двум участкам скользить вдоль продольной оси, но не перевести в других двух направлениях
Два вращательных, позволяя бедру вращаться о продольной оси (относительно голени), но не вращаться о других двух направлениях
universals соединение главной пластины к бедрам налагают четыре ограничения:
Три позиционных, требуя, чтобы были расположены две точки
Одно вращательное, препятствуя тому, чтобы бедро вращалось о его продольной оси (относительно главной пластины — не относительно голени)
Получение Независимого числа степеней свободы. Платформа Стюарта имеет 13 движущихся контактирующих тел. Без ограничений демонтированная платформа Стюарта имеет 13*6 = 78 чисел степеней свободы.
Сборка частей налагает 12*6 = 72 ограничения. Поэтому платформа Стюарта имеет 13*6 - 12*6 = 6 независимых чисел степеней свободы.
Запустите с платформы Стюарта как собранная модель Simscape Multibody.
Тела Без числа степеней свободы. Тело Simscape Multibody не несет числа степеней свободы. Вместо этого пары Тел соединяются Соединениями, которые выражают движения одного Тела относительно другого.
Шесть Территорий представляют опорную плиту. Тринадцать Тел представляют подвижные части.
Примитивы соединений как число степеней свободы. Каждое Соединение содержит примитивы. Поступательные и вращательные примитивы каждое специальное одна степень свободы. (Это единственные типы примитивов, используемые здесь.) Модель платформы Стюарта содержит 18 Соединений, содержащих 6*6 = 36 примитивов, из которых 30 являются вращательными, и 6 поступательны.
Шесть соединений Universal, соединяющих голени с основой. Каждый содержит два вращательных примитива.
Шесть соединений Cylindrical, соединяющихся ниже с бедрами. Каждый содержит вращательное и поступательный примитив.
Шесть соединений Universal, соединяющих бедра с главной пластиной. Каждый содержит два вращательных примитива.
Подсчет Циклов. Участки платформы Стюарта формируют шесть циклов, но только пять независимы. Можно получить топологически эквивалентную платформу путем выравнивания главной пластины и основы в линии и подсчета пяти циклов, которые имеют эти шесть участков как стороны:
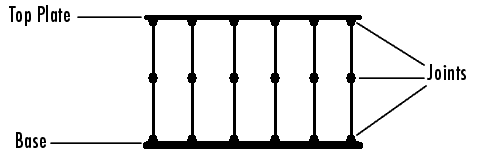
Сокращение Соединений Платформы Стюарта и Получение Дерева. Чтобы симулировать машину с замкнутыми циклами (как платформа Стюарта), симуляция Simscape Multibody заменяет его внутренне на эквивалентную машину (дерево охвата) полученный путем сокращения всех независимых циклов однажды и заменяющий сокращения на (невидимые) эквивалентные ограничения.
Получите дерево охвата путем сокращения пяти из шести верхних Universals. Этого сокращения как раз, чтобы открыть все циклы, но не отключить машину в непересекающиеся части. Дерево содержит 13 (неразрезанных) Соединений, составляющих 6* (2+2) + 2 = 26 чисел степеней свободы.
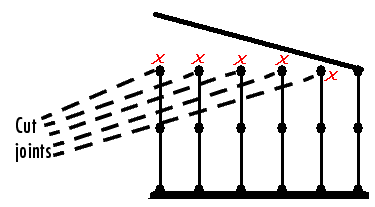
Наложение Сокращающих Ограничений и Получение Независимого числа степеней свободы. Чтобы завершить преобразование машины с обратной связью в эквивалентное дерево, наложите ограничения, чтобы заменить Соединения сокращения. Существует 20 таких ограничений. Каждое ограничение эквивалентно повторному прикреплению Соединения сокращения и анализирует в пять наборов
Три позиционных ограничения, требуя, чтобы были расположены две точки
Одно вращательное ограничение, препятствуя тому, чтобы бедро вращалось о его продольной оси относительно главной пластины
Таким образом повторное прикрепление Соединений сокращения, чтобы повторно собрать платформу уезжает 26 - 5*4 = 6 независимых чисел степеней свободы.
Эти шесть независимых чисел степеней свободы обычно берутся, чтобы быть шестью длинами участка. Любая степень свободы идентифицировала, здесь теперь зависит от этих шести длин. Каждый раз, когда вы изменяете длину, universals, соединение участков к основной и главной пластине вращается, главная пластина переключает и вращается, и бедра вращаются об их продольных осях.
Кроме того, и эквивалентно, можно взять шесть независимых чисел степеней свободы, чтобы быть шестью числами степеней свободы главной, мобильной пластины. Путем соединения главной пластины вы заменяете шесть независимых чисел степеней свободы неограниченной пластины с шестью числами степеней свободы под точным и устойчивым управлением системы позиционирования с шестью участками.
Шесть чисел степеней свободы связанной главной пластины не в дополнение к числу степеней свободы длины участка. Они - только эквивалентное, заменяющее описание тех же шести независимых чисел степеней свободы. Целая платформная система, когда-то полностью соединенная, всегда имеет точно шесть независимых степеней свободы.
Для получения дополнительной информации о соединениях, степени свободы и топология, рассматривают следующие разделы: