Фиксированный угол между осями Z двух систем координат
Ограничения

Этот блок применяет фиксированный угол между осями Z основы и систем координат порта последователя. Системы координат теряют одну вращательную степень свободы, если ограничительный угол больше 0 ° и меньший, чем 180 °. Они теряют две вращательных степени свободы, если ограничительный угол составляет точно 0 ° или 180 ° — то есть, если системы координат параллельны или антипараллельны. Рисунок показывает ограничительный угол между двумя системами.
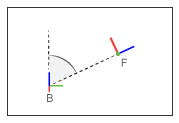
Угловой тип ограничения. Настройкой по умолчанию является General.
| Ввод | Цель |
|---|---|
Parallel | Выровняйте основу, и последователь структурируют +Z оси. |
Anti-Parallel | Выровняйте базовую систему координат +Z, ось с последователем структурируют-Z ось. |
Perpendicular | Сделайте основу, и последователь структурируют перпендикуляр осей Z друг другу. |
General | Содержите заданный угол между осями Z основы и систем координат порта последователя. |
Ограничительный угол между основой и последователем структурирует оси Z. Угол должен находиться в диапазоне 0 <θ <180 градусов. Для угла 0 или 180 градус, набор Type к Parallel или Anti-Parallel вместо этого. Значением по умолчанию является 45 градус.
Выберите, вычислить ли и вывести вектор крутящего момента ограничения расстояний и его величину. Крутящий момент ограничения расстояний является крутящим моментом, который должен применить блок для того, чтобы обеспечить угол, который вы задаете между основой и системами координат порта последователя.
Ограничение закручивает действие в парах. Как выражено третьим законом Ньютона движения, если основная система координат порта проявляет ограничительный крутящий момент на системе координат порта последователя, то система координат порта последователя должна проявить равный и противоположный крутящий момент на основной системе координат порта. Выберите который из двух ограничительных крутящих моментов, чтобы распознаться:
Follower on Base — Обнаружьте ограничительный крутящий момент, который система координат порта последователя проявляет на основной системе координат порта.
Base on Follower — Обнаружьте ограничительный крутящий момент, который основная система координат порта проявляет на системе координат порта последователя.
Блок выражает ограничительный вектор крутящего момента в терминах своих Декартовых векторных компонентов. Разделение вектора на векторные компоненты известно как векторное разрешение. Система координат, оси которой задают векторные направления компонента, известна как систему координат разрешения. Выберите, разрешить ли ограничительный вектор крутящего момента в основе или системе координат порта последователя.
Вычислите и выведите Декартовы компоненты углового ограничительного вектора крутящего момента. Выходной сигнал является 3D вектором с компонентами, выраженными об этих X, Y, и осях Z системы координат разрешения.
Вычислите и выведите величину углового ограничительного крутящего момента, включая его знак.
Блок обеспечивает два порта системы координат:
B Порт базовой системы координат
F Порт системы координат последователя
Кроме того, блок обеспечивает два выходных порта физического сигнала:
t Угловое ограничение закручивает вектор
TM — Величина со знаком углового ограничительного крутящего момента
Bevel Gear Constraint | Common Gear Constraint | Distance Constraint | Point on Curve Constraint | Rack and Pinion Constraint