interpolateПолиномиальной интерполяция
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
interpolate(xList,yList,X, <F>) interpolate(nodes,values,ind, <F>)
interpolate вычисляет интерполяционный многочлен через данные по прямоугольной сетке.
Вызов interpolate(xList, yList, X) с xList = [x1, …, xn] и yList = [y1, …, yn] возвращает полином степени меньше, чем n в переменной X который интерполирует точки (x 1, y 1), …, (x n, y n).
Этот вызов с 1-мерной сеткой xList эквивалентно соответствующему 'многомерному' вызову interpolate([xList], array(1..n, [yList]), [X]).
Для d - размерная интерполяция, примите, что indeterminates ind = [X 1, …, X d] задан. Интерполяционный многочлен P = poly (…, [X 1, …, X d], F) удовлетворяет
![]()
для всех точек![]() в сетке. P является полиномом минимальной степени, удовлетворяющей условиям интерполяции, т.е.
в сетке. P является полиномом минимальной степени, удовлетворяющей условиям интерполяции, т.е. degree(P, X i) <n i.
Только интерполируя значения в конкретных числовых точках X 1 = v 1, …, X d = v d требуется, мы рекомендуем не вычислить P с символьным indeterminates ind = [X 1, …, X d] и затем оценивает P (v 1, …, v d). Это быстрее, чтобы вычислить это значение непосредственно interpolate с ind = [v 1, …, v d]. См. Пример в качестве примера 1 и Пример 3.
Мы рассматриваем 1-мерную проблему интерполяции. К каждому узлу x i значение y сопоставлен i. Интерполяционный многочлен P с P (x i) = y i:
xList := [1, 2, 3]: yList := [y1, y2, y3]: P := interpolate(xList, yList, X)
![]()
Оценкой P в точке![]() дают:
дают:
evalp(P, X = 5/2)
![]()
Это значение может также быть вычислено непосредственно без символьного полинома:
interpolate(xList, yList, 5/2)
![]()
delete xList, yList, P:
Мы демонстрируем многомерную интерполяцию. Рассмотрите данные по следующим 2-мерным 2 ×3 сеткам:
XList := [1, 2]: YList := [1, 2, 3]: values := array(1..2, 1..3, [[1, 2, 3], [3, 2, 1]]): P := interpolate([XList, YList], values, [X, Y])
![]()
Затем интерполяция по 3-мерным 2 ×3×2 сеткам продемонстрирована:
L1 := [1, 2]: L2 := [1, 2, 3]: L3 := [1, 2]: values := array(1..2, 1..3, 1..2, [[[1, 4], [1, 2], [3, 3]], [[1, 4], [1, 3], [4, 0]]]): interpolate([L1, L2, L3], values, [X, Y, Z])
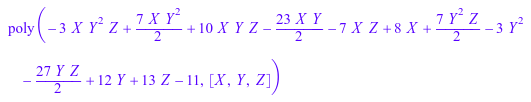
delete XList, values, P, L1, L2, L3:
Мы интерполируем данные по 2-мерной сетке:
n1 := 4: L1 := [i $ i = 1..n1]:
n2 := 5: L2 := [i $ i = 1..n2]:
f := (X, Y) -> 1/(1 + X^2 + Y^2):
values := array(1..n1, 1..n2,
[[f(L1[i], L2[j]) $ j=1..n2] $ i=1..n1]):Во-первых, мы вычисляем символьный полином:
P := interpolate([L1, L2], values, [X, Y])
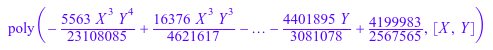
Фиксируя значение Y = 2.5, это дает к полиному в X.
evalp(P, Y = 2.5)
![]()
Это может также быть вычислено непосредственно при помощи точки оценки для неопределенного Y:
interpolate([L1, L2], values, [X, 2.5])
![]()
Если все indeterminates заменяются точками оценки, соответствующее значение интерполяции возвращено:
interpolate([L1, L2], values, [1.2, 2.5])
![]()
delete n1, n2, f, values, P:
Мы демонстрируем интерполяцию по специальному содействующему полю. Рассмотрите следующие данные по 2-мерным 2 ×3 сеткам:
XList := [3, 4]: YList := [1, 2, 3]: values := array(1..2, 1..3, [[0, 1, 2], [3, 2, 1]]):
Со следующим вызовом эти данные преобразованы в целые числа по модулю 7. Арифметика по этому полю используется:
F := Dom::IntegerMod(7): P := interpolate([XList, YList], values, [X, Y], F)
![]()
Оценка P в узлах решетки воспроизводит присваиваемые значения, преобразованные в поле:
evalp(P, X = XList[2], Y = YList[3]) = F(values[2, 3])
![]()
delete XList, YList, values, F, P:
|
Узлы: список |
|
Значения: список |
|
Неопределенное или арифметическое выражение. Неопределенным является любой идентификатор (доменного типа |
|
Список [L 1, …, L d] d перечисляет L i, задающий d - размерная прямоугольная сетка
Списки L i могут иметь различные длины n i = |Li |. Элементы каждого i L должны быть отличными. |
|
d - размерный
|
|
Список d indeterminates или арифметических выражений. Indeterminates являются любой идентификаторами (доменного типа |
|
Любой Возвращенный полином имеет тип Для поля Для |
Интерполяционный многочлен P доменного типа DOM_POLY в indeterminates, заданном ind по содействующему полю F возвращен. Элементы в ind это не indeterminates, но арифметические выражения не используются в качестве indeterminates в P, но вводят его коэффициенты: полином “оценен” в этих точках. Если никакой элемент ind неопределенное, значение полинома в точке, заданной ind возвращен. Это - элемент поля F или арифметическое выражение, если F = Expr.
Для d - размерная прямоугольная сетка
![]()
заданный списками
![]()
с присваиваемыми значениями
![]() ,
,
интерполяционный многочлен в indeterminates X 1, …, X d дают
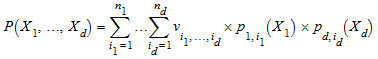
Лагранжевыми полиномами
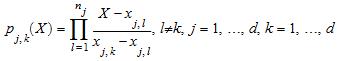
сопоставленный с k-th узел j-th координата.