`numeric`::`cubicSpline`

Интерполяция кубическими сплайнами

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

numeric::cubicSpline([x₀, y₀], [x₁, y₁], …, <BoundaryCondition>, <Symbolic>, <NoWarning>)
numeric::cubicSpline([x₀, x₁, …], [y₀, y₁, …], <BoundaryCondition>, <Symbolic>, <NoWarning>)
numeric::cubicSpline([[x₀, x₁, …], [y₀, y₁, …]], <BoundaryCondition>, <Symbolic>, <NoWarning>)

Описание

_{numeric::cubicSpline([x0, y0], [x1, y1], …)} возвращает кубическую функцию сплайна интерполяция последовательности координатных пар [x _i, y _i].

Вызов _{S := numeric::cubicSpline([x0, y0], …, [xn, yn])} дает к кубической функции сплайна S, интерполирующий данные [x ₀, y ₀], …, [x _n, y _n], т.е. S (x _i) = y _i для i = 0, …, n. Функция сплайна является кусочным полиномом степени ≤ 3 на интервалах. S и его первые две производные непрерывны в точках x ₁, …, x _{n - 1}. Обратите внимание на то, что S расширяет полиномиальное представление на, к и, соответственно.

По умолчанию, NotAKnot граничные условия приняты, т.е. третья производная непрерывна в точках x ₁ и x _{n - 1}. С этим граничным условием S является кубическим полиномом на интервалах и.

По умолчанию все входные данные преобразованы в числа с плавающей запятой. Это преобразование может быть подавлено опцией Symbolic.

Без опции Symbolic, абсциссы x _i должны быть числовыми действительными значениями в порядке возрастания. Если эти данные не упорядочены, то numeric::cubicSpline переупорядочивает абсциссы внутренне, выдавая предупреждение. Предупреждение может быть выключено опцией NoWarning.

Функциональный S возвращен numeric::cubicSpline может быть вызван один, два или три аргумента:

Вызов S(z) возвращает явное выражение или номер, если z вещественное число. В противном случае, символьный вызов S(z) возвращен.
Вызов S(z, [k]) с неотрицательным целочисленным k возвращает k-th производная S. См. Пример 4. Для k> 3, нуль возвращен для любого z.
Вызов S(z, i) предназначается для символьных аргументов z. Аргумент i должен быть целым числом. Внутренне, z принят, чтобы удовлетворить x _i ≤ z <x _{i + 1}, и S(z, i) возвращает многочленное выражение в z, представляющем функцию сплайна на этом интервале.
Вызов S(z, i, [k]) с целочисленным i и неотрицательным целочисленным k возвращает полиномиальное представление k-th производная функции сплайна на интервале x _i ≤ z <x _{i + 1}.

Если S сгенерирован с символьными абсциссами x _i (обязательно использующий опцию Symbolic), затем вызов S(z) с числовым z приводит к ошибке. Вызов S(z, i) должен использоваться в символьных абсциссах!

Примечание

Обратите внимание на то, что интерполяция 2 точек (x ₀, y ₀), (x ₁, y ₁) должна быть задана _{numeric::cubicSpline( [x0, y0] , [x1, y1] )}, не _{numeric::cubicSpline( [x0, x1] , [y0, y1] )}!

Примеры

Пример 1

Мы демонстрируем некоторые вызовы с числовыми входными данными:

data := [i, sin(i*PI/20)] $ i= 0..40:
S1 := numeric::cubicSpline(data):
S2 := numeric::cubicSpline(data, Natural):
S3 := numeric::cubicSpline(data, Periodic):
S4 := numeric::cubicSpline(data, Complete = [3, PI]):

В абсциссах воспроизводятся соответствующие входные данные:

float(data[6][2]), S1(5), S2(5), S3(5), S4(5)

Интерполяция между абсциссами зависит от граничного условия:

S1(4.5), S2(4.5), S3(4.5), S4(4.5)

Это кубические полиномы в z, задающем сплайн на интервале x ₀ = 0 ≤ z <x ₁ = 1:

expand(S1(z, 0)); expand(S2(z, 0));
expand(S3(z, 0)); expand(S4(z, 0))

delete data, S1, S2, S3, S4:

Пример 2

Мы демонстрируем некоторые вызовы с символьными данными:

S := numeric::cubicSpline([i, y.i] $ i = 0..3):

S(1/2)

Это - кубический полином в z, задающем сплайн на интервале x ₀ = 0 ≤ z <x ₁ = 1:

S(z, 0)

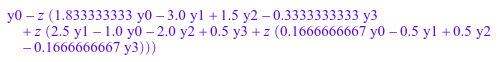
С опцией Symbolic, точная арифметика используется:

S := numeric::cubicSpline([i, y.i] $ i = 0..3, Symbolic):

S(1/2)

Также символьные граничные условия приняты:

S := numeric::cubicSpline([i, exp(i)] $ i = 0..10,
                               Complete = [a, b]):

S(0.1)

S := numeric::cubicSpline([0, y0], [1, y1], [2, y2],
                        Symbolic, Complete = [a, 5]):

collect(S(z, 0), z)

delete S:

Пример 3

Мы демонстрируем использование символьных абсцисс. Здесь опция Symbolic обязательно.

S := numeric::cubicSpline([x.i, y.i] $ i = 0..2, Symbolic):

Функция сплайна S может только быть вызван 2 аргументами. Это - кубический полином в z определение сплайна на интервале x ₀ ≤ z <x ₁:

S(z, 0)

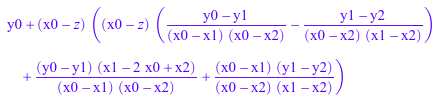
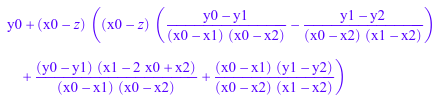
delete S:

Пример 4

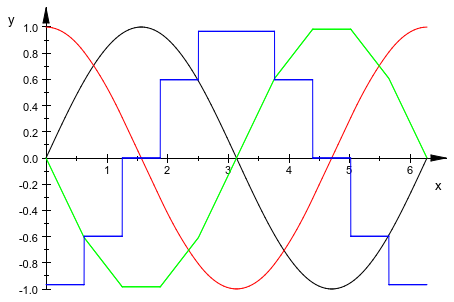
Мы строим функцию сплайна вместе с ее первыми тремя производными. Сплайн аппроксимирует функциональный sin (x):

n := 10:
x := array(0..n, [i/n*2*PI $ i = 0..n]):
S := numeric::cubicSpline([x[i], sin(x[i])] $ i = 0..n, Natural):
delete x:
plot(
   plot::Function2d(S(x), x = 0..2*PI, Color = RGB::Black),
   plot::Function2d(S(x, [1]), x = 0..2*PI, Color = RGB::Red),
   plot::Function2d(S(x, [2]), x = 0..2*PI, Color = RGB::Green,
                    Mesh = 1000),
   plot::Function2d(S(x, [3]), x = 0..2*PI, Color = RGB::Blue,
                    Mesh = 1000)
)

delete n, S:

Пример 5

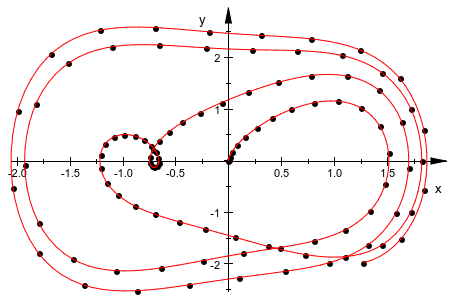
Мы демонстрируем, как сгенерировать график фазы дифференциального уравнения с начальными условиями. Во-первых, мы используем numeric::odesolve вычислить числовую сетку решения указывает с n + 1 равноотстоящий узел времени t ₀, …, t _n в интервале [0, 20]:

DIGITS := 4: n := 100:
for i from 0 to n do t[i] := 20/n*i: end_for:
f := (t, x) -> [x[2], sin(t) - x[1]^3]:
x[0] := 0: y[0] := 0:
for i from 1 to n do
  [x[i], y[i]] := 
  numeric::odesolve(t[i-1]..t[i], f, [x[i-1], y[i-1]]):
end_for:

Сетка графика фазы состоит из следующих моментов:

Plotpoints := [[x[i], y[i]] $ i = 0..n]:

Мы хотим соединить эти точки сплайновой кривой. Мы задаем сплайн меж-Польша Sx (t), аппроксимирующий решение x (t) путем интерполяции данных [t ₀, x ₀], …, [t _n, x _n]. Сплайн меж-Польша Sy (t) аппроксимация получен путем интерполяции данных [t ₀, y ₀], …, [t _n, y _n]:

Sx := numeric::cubicSpline([t[i], x[i]] $ i = 0..n):
Sy := numeric::cubicSpline([t[i], y[i]] $ i = 0..n):

Наконец, мы строим точки mesh вместе со сплайновой кривой интерполяции:

plot(
     plot::PointList2d(Plotpoints, PointColor = RGB::Black),
     plot::Curve2d([Sx(z), Sy(z)], z = 0..20, Mesh = 5*(n - 1) + 1,
                    LineColor = RGB::Red)
    )

Функции plot::Ode2d и plot::Ode3d служите для отображения числовых решений ОДУ. На самом деле они реализованы, как обозначено предыдущими командами. Следующий вызов производит тот же график:

plot(plot::Ode2d(
 [t[i] $ i = 0..n], f, [x[0], y[0]],
 [(t, x) -> [x[1], x[2]], Style = Points, Color = RGB::Black],
 [(t, x) -> [x[1], x[2]], Style = Splines, Color = RGB::Red])):

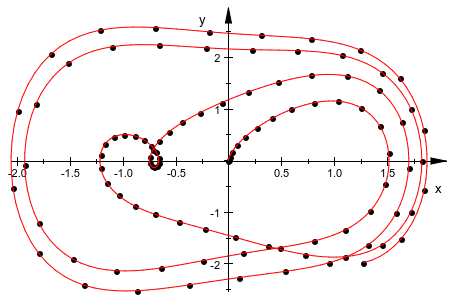
delete DIGITS, n, i, t, f, x, y, Plotpoints, Sx, Sy:

Параметры

`_{x0, x1, …}`	Числовые действительные значения в порядке возрастания
`_{y0, y1, …}`	Произвольные выражения
`BoundaryCondition`	Тип граничного условия: любой `NotAKnot`, `Natural`, `Periodic`, или `Complete = [a, b]` с произвольными арифметическими выражениями `a, b`.

Опции

`Symbolic`	При использовании этой опции не происходит никакое преобразование входных данных к числам с плавающей точкой. Приняты символьные абсциссы x _i. Упорядоченное расположение x ₀ <x ₁ <… <x _n принято `numeric::cubicSpline`. Это упорядоченное расположение не проверяется, даже если абсциссы являются числовыми!
`NoWarning`	x - значения точек интерполяции должны быть в порядке возрастания. Если входные данные нарушают это условие, стандартная программа выдает предупреждение и переупорядочивает данные автоматически. При использовании этой опции выключено предупреждение.
`NotAKnot`	С граничным условием по умолчанию `NotAKnot`, третья производная функции сплайна непрерывна в точках x ₁ и x _{n - 1}. С этим граничным условием S является полиномом на интервалах и.
`Natural`	Граничное условие `Natural` производит функцию сплайна удовлетворение S.
`Periodic`	Граничное условие `Periodic` производит функцию сплайна S, удовлетворяющий S (x ₀) = S (x _n). При использовании этой опции, входные данные y ₀, y _n должен совпасть, в противном случае ошибка повышена.
`Complete`	Опция, заданная как `Complete = [a, b]` Граничное условие `Complete = [a, b]` производит функцию сплайна удовлетворение S. Символьные данные `a, b` приняты.

Документация