isolateИзолируйте переменную или выражение от уравнения
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
isolate(eq, expr)
isolate(eq, expr) перестраивает уравнение eq так, чтобы выражение expr появляется на левой стороне. Результат похож на решение eq для expr. Однако isolate возвращает только одно решение, даже если существуют несколько решений. Если isolate не может изолировать expr от eq, это перемещает все условия, содержащие expr к левой стороне. Можно использовать выход isolate как введено к subs устранить expr от eq.
Если eq не имеет никакого решения, isolate возвращает ошибку. isolate функция также игнорирует особые регистры. Если единственные решения eq особые случаи, затем isolate игнорирует те особые регистры и возвращает ошибку. Кроме того, если возвращенное решение содержит параметры, параметры не могут быть допустимыми для особых случаев.
Вы не можете задать expr как математическая константа, такая как PI, ЭЙЛЕР, и так далее.
По умолчанию, isolate(eq, expr) возвращает только решения, сопоставимые со свойствами expr.
Если вход содержит числа с плавающей запятой, решатель заменяет их аппроксимированными рациональными значениями. Точность этих приближенных значений зависит от переменной окружения DIGITS. Если isolate находит решение, MuPAD® внутренне вызывает float функция для того решения, и затем возвращает результат.
isolate реагирует на свойства идентификаторов.
Изолированный x от уравнения a*x^2 + b*x + c = 0.
eqn := a*x^2 + b*x + c = 0: xSol := isolate(eqn, x)
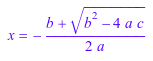
Даже при том, что уравнение имеет несколько решений, isolate возвращает только одно решение.
Устраните x от eqn путем вызова subs заменять x использование xSol.
subs(eqn, xSol)
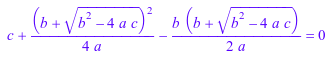
Можно также изолировать выражения. Изолированный x(t) от следующего уравнения.
isolate(a*x(t)^2 + b*c = 0, x(t))
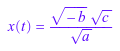
Изолированный a*x(t) от того же уравнения.
isolate(a*x(t)^2 + b*c = 0, a*x(t))
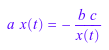
Если isolate не может найти символьное решение, оно возвращает ошибку. Поскольку isolate не возвращает особые случаи, это также возвращает ошибку, если единственные решения являются особыми случаями.
Сравните isolate с solve для уравнения, чье только решение является особым случаем.
solve(x = x+a, x); isolate(x = x+a, x)
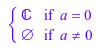
Error: Unable to isolate 'x' because the equation has no solution. [isolate]
solve возвращает особый случай в то время как isolate игнорирует особый регистр и возвращает ошибку.
Для уравнений с несколькими решениями, isolate возвращает 'самое простое' решение.
Изолированный x от уравнений со многими решениями продемонстрировать это поведение isolate.
isolate(cos(x) = x, x)
![]()
isolate(x^2 = 1, x)
![]()
isolate(sin(x) = 0, x)
![]()
isolate(sqrt(x) = C, x)
![]()
isolate только возвращает результаты, совместимые с предположениями на переменной, которая будет изолирована. Например, примите тот x представляет действительное отрицательное число. Затем изолируйте его от следующего уравнения.
assume(x, Type::Negative): isolate(x^4 = 1, x)
![]()
Удалите предположение. isolate выбирает различное решение возвратиться.
unassume(x): isolate(x^4 = 1, x)
![]()
Если вход содержит числа с плавающей запятой, MuPAD вызывает float функция для полученного решения.
Изолированный x от уравнения с числами с плавающей запятой.
isolate(x^3 + 3.0*x + 1 = 0, x)
![]()
Можно изолировать выражение в уравнении символьными параметрами. isolate функция возвращает общее решение, где значения параметров, как гарантируют, не будут содержать для особых случаев.
Изолированный x в уравнении.
isolate(a*x^2/(x-a) = 1, x)
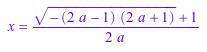
Возвращенное значение x не содержит в особом случае тот параметр a имеет значение 0.
|
Уравнение. |
|
Переменная или выражение, которое будет изолировано. |
isolate(eq, expr) возвращает уравнение, где правая сторона не содержит переменную или выражение, которое будет изолировано. isolate не вводит недавно сгенерированные параметры. Возвращенное уравнение всегда является допустимым входом к subs..
RootOf | float | lhs | linsolve | numeric::linsolve | numeric::solve | rhs | solve