linsolveРешите систему линейных уравнений
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
linsolve(eqs,options) linsolve(eqs,vars,options)
linsolve(eqs, vars) решает систему линейных уравнений относительно неизвестных vars.
linsolve(eqs, < vars , < ShowAssumptions >>) решает линейную систему eqs относительно неизвестных vars. Если никакие неизвестные не заданы, то linsolve решает для всего indeterminates в eqs; неизвестные определяются внутренне indets(eqs,PolyExpr).
linsolve(eqs, vars, Domain = R) решает систему по доменному R, который должен быть полем, т.е. областью категории Cat::Field.
Обратите внимание на то, что формат возврата не позволяет возвращать элементы ядра если элементы доменного R не может быть умножен с символьными неизвестными, которые охватывают ядро. В таком случае, linsolve выдает предупреждение и возвращает только специальное решение. Ядро может быть вычислено через linalg::matlinsolve для любого поля R.
Каждый элемент eqs должно быть или уравнение или арифметическое выражение f, который считается эквивалентным уравнению f = 0.
Неизвестные в vars не должны быть идентификаторы или индексированные идентификаторы; выражения, такие как sin(x), f(x), или y^(1/3) позволены также. В более общем плане, любое выражение, принятое как неопределенный poly допустимое неизвестное.
Если опция ShowAssumptions не дан и система разрешима, затем возвращаемое значение является списком уравнений формы var = value, где var одни из неизвестных в vars и value арифметическое выражение, которое не включает ни одних из неизвестных на левой стороне возвращенного уравнения. Обратите внимание на то, что, если коллектор решения имеет размерность, больше, чем нуль, то некоторые неизвестные в vars произойдет на правой стороне некоторых возвращенных уравнений, представляя степени свободы. Смотрите Пример 2.
Если vars список, затем решенные уравнения возвращены в тот же порядок как неизвестные в vars.
Функциональный linsolve может только решить системы линейных уравнений. Используйте solve для нелинейных уравнений.
linsolve функция интерфейса к процедурам numeric::linsolve и linalg::matlinsolve. Для получения дополнительной информации смотрите numeric::linsolve, linalg::matlinsolve страницы справки и фоновый раздел этой страницы справки.
Система eqs проверяется на линейность. Поскольку такой тест может быть дорогим, рекомендуется использовать numeric::linsolve или linalg::matlinsolve непосредственно, когда вы знаете, что система линейна.
Уравнения и переменные могут быть введены как наборы или списки:
linsolve({x + y = 1, 2*x + y = 3}, {x, y}),
linsolve({x + y = 1, 2*x + y = 3}, [x, y]),
linsolve([x + y = 1, 2*x + y = 3], {x, y}),
linsolve([x + y = 1, 2*x + y = 3], [x, y])![]()
Также выражения могут использоваться в качестве переменных:
linsolve({cos(x) + sin(x) = 1, cos(x) - sin(x) = 0},
{cos(x), sin(x)})![]()
Кроме того, индексируемые идентификаторы допустимы, также:
S := linsolve({2*a[1] + 3*a[2] = 5, 7*a[2] + 11*a[3] = 13,
17*a[3] + 19*a[1] = 23}, {a[1], a[2], a[3]})![]()
Присвойте отдельные решения переменных с помощью assign. В качестве альтернативы получите доступ к решению путем индексации в S:
assign(S): a[1]; a2_val := S[2][2];
![]()
![]()
Удалите a для использования в дальнейших расчетах.
delete a;
Затем мы демонстрируем использование опции Domain и решите систему по полю ℤ 23 с ним:
linsolve([2*x + y = 1, -x - y = 0],
Domain = Dom::IntegerMod(23))![]()
Следующая система не имеет решения:
linsolve({x + y = 1, 2*x + 2*y = 3}, {x, y})![]()
Если решение линейной системы не уникально, то некоторые неизвестные используются в качестве “свободных параметров” охват пробела решения. В следующем примере неизвестный z такой параметр. Это не появляется на левой стороне решенных уравнений:
eqs := [x + y = z, x + 2*y = 0, 2*x - z = -3*y, y + z = 0]:
vars := [w, x, y, z]:
linsolve(eqs, vars)
![]()
Если вы используете Normal опция, linsolve вызывает normal функция для конечных результатов. Этот вызов гарантирует тот linsolve возвращает результаты в нормированной форме:
linsolve([x + a*y = a + 1, b*x - y = b - 1], {x, y})![]()
Если вы задаете Normal = FALSElinsolve не вызывает normal для конечного результата:
linsolve([x + a*y = a + 1, b*x - y = b - 1], {x, y}, Normal = FALSE)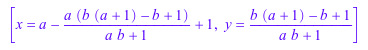
Решите эту систему:
eqs := [x + a*y = b, x + A*y = b]:
linsolve(eqs, [x, y])
![]()
Обратите внимание на то, что больше решений существует для a = Alinsolve не использует эти решения, потому что это делает некоторые дополнительные предположения на символьных параметрах этой системы. Видеть предположения что linsolve сделанный при решении этой системы, используйте ShowAssumptions опция:
linsolve(eqs, [x, y], ShowAssumptions)
![]()
delete eqs:
|
Список или набор линейных уравнений или арифметических выражений |
|
Список или набор неизвестных, чтобы решить для: обычно идентификаторы или индексированные идентификаторы |
|
Опция, заданная как Решите систему по полю |
|
Опция, заданная как Возвратите нормированные результаты. Значение По умолчанию, Чтобы избежать этого дополнительного вызова, задайте |
|
Возвратите информацию о внутренних предположениях что При использовании этой опции, Когда Исключение Гаусса производит уравнение |
Без ShowAssumptions опция, список упрощенных уравнений возвращен. Это представляет общее решение системы eqs. FAIL возвращен, если система не разрешима.
С ShowAssumptions, список [Solution, Constraints, Pivots] возвращен. Solution список упрощенных уравнений, представляющих общее решение eqs. Списки Constraints и Pivots содержите уравнения и неравенства, вовлекающие символьные параметры в eqs. Внутренне, они были приняты, чтобы сохраняться при решении системы.
Если опция Domain не присутствует, система решена путем вызова numeric::linsolve с опцией Symbolic.
Если опция Domain = R дан и R любой Dom::ExpressionField() или Dom::Float, затем numeric::linsolve используется для расчета решение системы. Эта функция использует разреженное представление уравнений.
В противном случае, eqs сначала преобразован в матрицу и затем решен linalg::matlinsolve. Возможно разреженная структура входной системы не учтена.