numeric::solveЧисловое решение уравнений (атрибут плавающий решают),
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
numeric::solve(eqs, <vars>,options) float(holdsolve(eqs, <vars>,options)) float(freezesolve(eqs, <vars>,options))
numeric::solve вычисляет числовые решения уравнений. Для полиномиальных уравнений возвращены все решения. Для неполиномиальных уравнений только одно решение, если таковые имеются, возвращено если опция AllRealRoots используется.
Обратите внимание на то, что только для полиномиальных/рациональных уравнений все решения разыскиваются. Для non-polynomial/non-rational уравнений только одно решение, если таковые имеются, возвращено если опция AllRealRoots используется.
Если уравнения содержат немногочленные выражения, в целом не возможно изолировать все корни численно. Думайте об уравнениях, таких как
это, имеют бесконечно много действительных решений вокруг источника! Если полный набор всех действительных решений одного non-polynomial/non-rational уравнения в одном неизвестном желаем, можно попробовать опцию AllRealRoots. При использовании этой опции, эвристика пытается изолировать все действительные решения уравнения. Это, однако, просто heuristical: нет никакой суровости в алгоритме, и не гарантируется, что все решения найдены. В качестве альтернативы можно также использовать стандартный numeric::realroots изолировать интервалы, в которых могут существовать решения.
numeric::solve простая функция интерфейса, объединяющая функциональность числовых решателей numeric::fsolve, numeric::linsolve, numeric::polyroots, и numeric::polysysroots. Формат возврата этих стандартных программ изменяется, чтобы сделать его сопоставимым с возвращаемыми значениями символьного решателя solve.
Можно вызвать специализированные числовые решатели непосредственно. Однако обратите внимание, что возврат вводит характерный для каждого из этих решателей.
numeric::solve классифицирует уравнения можно следующим образом:
Если eqs одно одномерное полиномиальное уравнение, затем оно непосредственно передается numeric::polyroots. См. Пример 2. Корни возвращены как набор или как Dom::Multiset если Multiple используется.
Если eqs многомерное полиномиальное уравнение или список или набор таких уравнений, затем уравнения и соответствующие дополнительные аргументы передаются любому numeric::linsolve или numeric::polysysroots. См. Пример 3. Корни возвращены как набор или как Dom::Multiset если Multiple используется.
Рациональное уравнение или набор или список рациональных уравнений заменяются его числителем (числителями). Такие уравнения обрабатываются как полиномиальные уравнения.
Если eqs non-polynomial/non-rational уравнение или набор или список, содержащий такое уравнение, затем уравнения и соответствующие дополнительные аргументы передаются числовому решателю numeric::fsolve.
Для неполиномиальных уравнений только один числовой корень возвращен, если AllRealRoots задан! См. Пример 4.
Для неполиномиальных уравнений не должно быть большего количества уравнений, чем неизвестные!
Используя Multiple поскольку неполиномиальные уравнения приводят к ошибке, если опция AllRealRoots задан, также!
Для систем многомерных неполиномиальных уравнений MuPAD® использует поиск Ньютона. Это должно смочь оценить частные производные уравнений относительно переменных, которые будут решены для.
Для одного одномерного уравнения сначала bisectioning схема с квадратичной интерполяцией используется, который не требует никакого дифференцирования уравнения. Если это не успешно, поиск Ньютона запускается, который требует производной включенных функций.
Для удобства, также полиномы доменного типа DOM_POLY приняты, везде, где уравнение ожидается.
В отличие от символьного решателя solve, числовой решатель не реагирует на свойства набора идентификаторов через assume. Единственное исключение, где numeric::solve реагирует на свойства идентификаторов, для систем полиномиальных уравнений (только там, где существует больше чем одна переменная).
Чтобы реагировать на свойства идентификаторов, вместо этого вызовите float ( hold( solve )(arguments)).
Если пользователь не задает indeterminates, который будет решен для, то indeterminates внутренне выбраны numeric::indets(eqs).
Начальные точки, такие как x = a или поиск располагается, такие как x = a..b заданный в vars проигнорированы если eqs полиномиальное уравнение или система полиномиальных уравнений.
Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Следующие три вызова решателя эквивалентны:
eqs := {x^2 = sin(y), y^2 = cos(x)}:
numeric::solve(eqs, {x, y}),
float(hold(solve)(eqs, {x, y})),
float(freeze(solve)(eqs, {x,y}))
delete eqs:
Мы демонстрируем корневой поиск одномерных полиномов:
numeric::solve(x^6 - PI*x^2 = sin(3), x)
Полиномы типа DOM_POLY может использоваться в качестве входа:
numeric::solve(poly((x - 1/3)^3, [x]), x)
С Multiple, Dom::Multiset возвращен, указав на кратность корня:
numeric::solve(x^3 - x^2 + x/3 -1/27, x, Multiple)
Мы демонстрируем корневой поиск полиномиальных систем. Обратите внимание на то, что символьный решатель solve включен, если система нелинейна. Приняты символьные параметры:
numeric::solve({x^2 + y^2 = 1, x^2 - y^2 = exp(z)}, {x, y})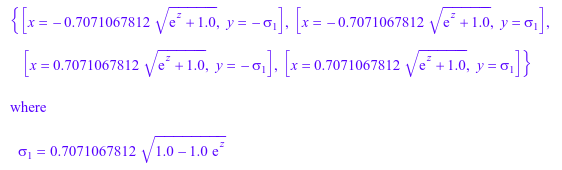
Мы демонстрируем корневой поиск неполиномиальных уравнений. Без опции AllRealRoots, только одно решение разыскивается:
eq := exp(-x) - 10*x^2: numeric::solve(eq, x)
Начиная с numeric::solve только вызывает корневое средство поиска numeric::fsolve, можно также использовать эту стандартную программу непосредственно. Отметьте различный выходной формат:
numeric::fsolve(eq, x)
Входной синтаксис numeric::solve и numeric::fsolve идентичные, т.е. начальные точки, поисковые области значений и опции могут использоваться. Например, другое решение предыдущего уравнения найдено ограниченным поиском на интервале
:
numeric::solve(eq, x = -1..0, RestrictedSearch)
Мы используем опцию AllRealRoots изолировать все действительные решения уравнения:
numeric::solve(eq, x, AllRealRoots)
Со следующим вызовом мы ограничиваем поиск отрицательной полуосью:
numeric::solve(eq, x = -infinity..0, AllRealRoots)
Для следующей системы, numeric::solve находит решение с положительным y:
eqs := [exp(x) = 2*y^2, sin(y) = y*x^3]: numeric::solve(eqs, [x, y])
Другое решение с отрицательным y найдено с соответствующей поисковой областью значений:
numeric::solve(eqs, [x = 1, y = -infinity..0])
delete eq, eqs:
|
Уравнение, список, набор, |
|
Неизвестное, список неизвестных или набор неизвестных. Неизвестные могут быть идентификаторами или индексированными идентификаторами. Также уравнения формы |
|
Только использоваться если ПримечаниеОбратите внимание на то, что нет никакой гарантии, что все действительные решения будут найдены. Примечание Арифметика интервала используется, чтобы изолировать поисковые интервалы для решений. Выражения в ПримечаниеУравнение должно подойти для оценки с арифметикой интервала. Смотрите С Это, настоятельно рекомендуют задать поисковый интервал вызовом, таким как Поиск всех действительных решений может быть очень трудоемким! |
|
Только использоваться если Это изменяет тип возврата от |
|
Только использоваться если Это передается |
|
Только использоваться если Это передается |
|
Только использоваться если Это передается |
|
Числовой поиск ограничивается поисковыми диапазонами, указанными в Эта опция передается Смотрите |
|
Числовой поиск может возвратить результаты вне поисковых диапазонов, указанных в Эта опция передается Смотрите |
|
Только использоваться в неполиномиальных уравнениях в сочетании с Это передается |
|
Только использоваться в неполиномиальных уравнениях. При использовании этой опции, несколькими вызовами Это передается |
|
Эта опция только оказывает влияние, когда она используется в полиномиальных уравнениях в сочетании с ПримечаниеЭта опция оказывает влияние если В таком случае эта опция передается |
Набор числовых решений. С опцией Multiple, набор доменного типа Dom::Multiset возвращен.