laplacianЛапласиан
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
laplacian(f,[x1, x2, …]) laplacian(f,[x1, x2, …],ogCoord, <c>)
laplacian(f, [ x1, x2, ...]) вычисляет Лапласиан![]() , т.е. div (grad (f)), функционального f = f (x 1, x 2, …) в Декартовых координатах x 1, x 2, ….
, т.е. div (grad (f)), функционального f = f (x 1, x 2, …) в Декартовых координатах x 1, x 2, ….
Таблица linalg::ogCoordTab обеспечивает некоторые предопределенные 3D преобразования прямоугольной координаты. В настоящее время его записями является Cartesian, Cylindrical, Spherical, Spherical[LeftHanded], EllipticCylindrical, ParabolicCylindrical, RotationParabolic, и Torus. Смотрите linalg::ogCoordTab для деталей. Например, команда
laplacian(f(r, Theta, phi), [r, Theta, phi], Spherical)
производит Лапласиан f в сферических координатах r, θ, ϕ, заданный преобразованием
![]() .
.
Произвольные ортогональные системы u = (u 1, …, u n) (в любой размерности n) могут использоваться путем передачи соответствующих “масштабных коэффициентов” в качестве третьего аргумента к laplacian. Они определяются следующим образом. Позвольте![]() быть Декартовыми координатами, позволить
быть Декартовыми координатами, позволить![]() быть orthognal преобразованием (т.е. векторы
быть orthognal преобразованием (т.е. векторы![]() являются ортогональными). Евклидовы длины
являются ортогональными). Евклидовы длины![]() векторов задают “шкалы”. Список s = [s 1, …, s n] может быть передан в качестве третьего аргумента
векторов задают “шкалы”. Список s = [s 1, …, s n] может быть передан в качестве третьего аргумента laplacian. Например, обычные двумерные полярные координаты x = r cos (ϕ), y = r sin (ϕ) приводят к масштабным коэффициентам
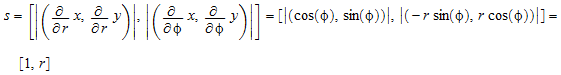 .
.
Таким образом, laplacian(f(r, phi), [r, phi], [1, r]) производит Лапласиан f (r, ϕ) в полярных координатах r и ϕ.
Вычислите Лапласиан в Декартовых координатах:
laplacian(f(x[1], x[2]), [x[1], x[2]])
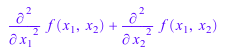
laplacian(x^2*y + c*exp(y) + u*v^2, [x, y, u, v])
![]()
Вычислите Лапласиан в цилиндрических координатах (r, ϕ, z) данный
![]() .
.
expand(laplacian(f(r, phi, z), [r, phi, z], Cylindrical))
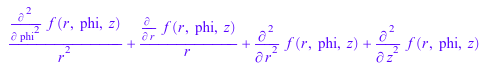
laplacian(r*cos(phi)*z^3, [r, phi, z], Cylindrical)
![]()
Передача имени Cylindrical из ортогональной системы, предопределенной в linalg::ogCoordTab самый простой способ использовать цилиндрические координаты. В качестве альтернативы можно передать соответствующие 'масштабные коэффициенты' явным образом. Они хранятся в linalg::ogCoordTab и может быть назван следующим образом:
linalg::ogCoordTab[Cylindrical, Scales](r, phi, z)
![]()
laplacian(r*cos(phi)*z^3, [r, phi, z], %)
![]()
Рассмотрите координаты Торуса (r, θ, ϕ) введенный
![]() .
.
Здесь, c является вещественной константой и 0 ≤ r <c, 0 ≤ θ ≤ 2 π, 0 ≤ ϕ ≤ 2 π принят. “Масштабные коэффициенты” хранятся в linalg::ogCoordTab:
linalg::ogCoordTab[Torus, Scales](r, thet, phi, c)
![]()
Лапласиан функционального f (r, ϕ, z) = r в этих координатах:
laplacian(r, [r, thet, phi], %)
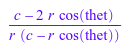
Можно ввести новые ортогональные системы. Например, рассмотрите ортогональные “координаты с 6 сферами” (u, v, w) введенный
![]() .
.
Это преобразование![]() не хранится в
не хранится в linalg::ogCoordTab, следовательно соответствующие “масштабные коэффициенты” метрики должны быть вычислены сначала:
![]() .
.
С этими “шкалами” Лапласиан может быть вычислен через laplacian:
s := 1/(u^2 + v^2 + w^2): factor(laplacian(f(u, v, w), [u, v, w], [s, s, s]))
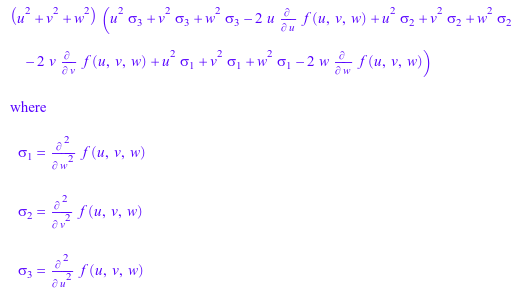
Поскольку Лапласиан является расхождением градиента, можно вычислить его следующим образом, также:
divergence(gradient(f(u, v, w), [u, v, w], [s, s, s]),
[u, v, w], [s, s, s])
expand(% - %2)
![]()
delete s:
|
Арифметическое выражение в переменных |
| |
|
Имя 3D системы прямоугольной координаты предопределено в таблице |
|
Параметр систем координат EllipticCylindrical и Торус, соответственно: арифметическое выражение. Значением по умолчанию является |
Арифметическое выражение.
Прямоугольные координаты![]() на ℝ n заданы преобразованием
на ℝ n заданы преобразованием![]() к Декартовым координатам
к Декартовым координатам![]() на ℝ n. Метрическим тензором, сопоставленным с координатами
на ℝ n. Метрическим тензором, сопоставленным с координатами![]() , дают
, дают
![]() .
.
Лапласиан функционального f дан расхождением
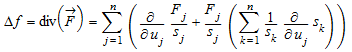 ,
,
где![]() компоненты градиента
компоненты градиента![]() .
.