gradientВекторный градиент
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
gradient(f,x) gradient(f,x,ogCoord, <c>)
gradient(f, x) вычисляет векторный градиент скалярной функции
относительно
в Декартовых координатах. Это - вектор
.
ogCoord может быть имя 3D системы прямоугольной координаты, предопределенной в таблице linalg::ogCoordTab. Смотрите пример 2.
В качестве альтернативы ogCoord может быть список вектора алгебраических выражений, представляющих масштабные коэффициенты системы координат. Смотрите Пример в качестве примера 3. Для получения дополнительной информации см. описание Scales опция на linalg::ogCoordTab страница.
Вычислите векторный градиент скалярной функции f (x, y) = x 2 + y в Декартовых координатах:
delete x, y: gradient(x^2 + y, [x, y])
Вычислите градиент функционального f (r, ϕ, z) = r cos (ϕ) z (0 ≤ ϕ <2π) в цилиндрических координатах:
delete r, z, phi: gradient(r*cos(phi)*z, [r, phi, z], Cylindrical)
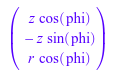
Вычислите градиент функционального f (r, ϕ, θ) = r sin (ϕ) cos (θ) в сферических координатах, данных
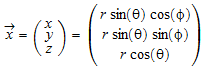
с 0 ≤ θ ≤ π, 0 ≤ ϕ <2 π.
Векторы
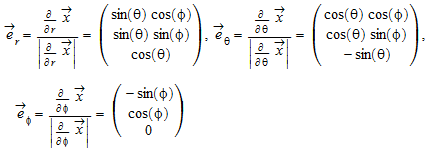
сформируйте ортогональную систему в сферических координатах.
Масштабные коэффициенты соответствующего координатного преобразования (см. linalg::ogCoordTab): 
который мы используем в следующем примере, чтобы вычислить градиент функционального f в сферических координатах:
delete r, Theta, phi:
gradient(r*sin(phi)*cos(Theta), [r, Theta, phi],
[1, r, r*sin(Theta)])
Сферические координаты уже заданы в linalg::ogCoordTab. Последний результат может также быть достигнут с входом gradient(r*sin(phi)*cos(Theta), [r, Theta, phi], Spherical):
gradient(r*sin(phi)*cos(Theta),
[r, Theta, phi],
Spherical)
|
Арифметическое выражение в переменных, данных в |
|
Список (индексируемых) идентификаторов |
|
Имя 3 размерных систем прямоугольной координаты предопределено в таблице |
|
Параметр систем координат EllipticCylindrical и Торус, соответственно: арифметическое выражение. Значением по умолчанию является |
Вектор-столбец доменного Dom::Matrix().