linalg::ogCoordTabТаблица преобразований прямоугольной координаты
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
linalg::ogCoordTab[ogName](u1,u2,u3, <c>) linalg::ogCoordTab[ogName, Transformation](u1,u2,u3, <c>) linalg::ogCoordTab[ogName, InverseTransformation](u1,u2,u3, <c>) linalg::ogCoordTab[ogName, UnitVectors](u1,u2,u3, <c>) linalg::ogCoordTab[ogName, Scales](u1,u2,u3, <c>) linalg::ogCoordTab[ogName, Ranges](<c>) linalg::ogCoordTab[ ogName , Dimension]
linalg::ogCoordTab таблица предопределенных преобразований прямоугольной координаты в
.
Запись сопоставлена с ogName задает координатное преобразование
, которое сопоставляет ортогональные параметры
с вектором
в Декартовых координатах.
Системы координат EllipticCylindrical и Torus заданы постоянным параметром c который должен быть передан в качестве дополнительного аргумента. Смотрите Пример 2.
Следующие координатные преобразования хранятся в linalg::ogCoordTab. Они являются обратимыми для обозначенных значений параметров:
Cartesian:
u 1 ∈ ℝ, u 2 ∈ ℝ, u 3 ∈ ℝ:
.
Spherical:
0 <u 1 <∞, 0 ≤ u 2 ≤ π, 0 ≤ u 3 <2π:
.
Spherical[LeftHanded]:
0 <u 1 <∞, 0 ≤ u 2 <2 π, 0 ≤ u 3 ≤ π:
.
Cylindrical:
0 <u 1 <∞, 0 ≤ u 2 <2 π, u 3 ∈ ℝ:
.
EllipticCylindrical:
0 <u 1 <∞, 0 ≤ u 2 <2 π, u 3 ∈ ℝ (с вещественной константой c):
.
ParabolicCylindrical:
0 <u 1 <∞, u 2 ∈ ℝ, u 3 ∈ ℝ:
.
RotationParabolic:
0 <u 1 <∞, 0 <u 2 <∞, 0 ≤ u 3 <2 π:
.
Torus:
0 <u 1 <c, 0 ≤ u 2 <2 π, 0 ≤ u 3 <2 π (с положительным постоянным c):
.
linalg::ogCoordTab используется функциями, такими как curlрасхождениеградиент, и laplacian выполнять расчеты в недекартовых координатах.
Следующий вызов возвращает Декартов вектор
в терминах предназначенных для правой руки сферических координат
:
linalg::ogCoordTab[Spherical, Transformation](u1, u2, u3)
Сферические координаты выражаются Декартовыми координатами:
linalg::ogCoordTab[Spherical, InverseTransformation](x, y, z)
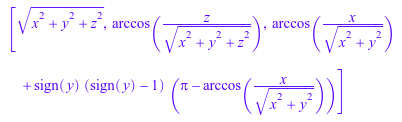
Отметьте sign(y) в выражении для u 3. Это гарантирует, что правильный угол возвращен для любого значения y:
assume(y > 0): linalg::ogCoordTab[Spherical, InverseTransformation](x, y, z)
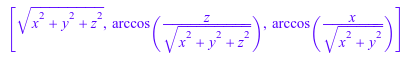
linalg::ogCoordTab[Spherical, InverseTransformation](1, 1, 0), linalg::ogCoordTab[Spherical, InverseTransformation](-1, 0, 1), linalg::ogCoordTab[Spherical, InverseTransformation](1, 0, 2), linalg::ogCoordTab[Spherical, InverseTransformation](1, -1, 3)
Эти значения параметров из следующих областей значений:
linalg::ogCoordTab[Spherical, Ranges]()
Следующие ортонормированные векторы являются касательной к сферическим линиям параметра:
linalg::ogCoordTab[Spherical, UnitVectors](u1, u2, u3)
'Масштабные коэффициенты':
linalg::ogCoordTab[Spherical,Scales](u1, u2, u3)
Существует следующее отношение между якобианом преобразования
от прямоугольных координат до Декартовых координат:
xyz:= linalg::ogCoordTab[Spherical, Transformation](u1, u2, u3): unitvectors:= linalg::ogCoordTab[Spherical, UnitVectors](u1, u2, u3): scales:= linalg::ogCoordTab[Spherical, Scales](u1, u2, u3):
linalg::transpose(jacobian(xyz, [u1, u2, u3])) = matrix(3, 3, scales, Diagonal)* matrix(unitvectors)
delete y, xyz, unitvectors, scales:
Следующий вызов возвращает Декартов вектор
в терминах эллиптических цилиндрических координат
, включающих параметр c:
linalg::ogCoordTab[EllipticCylindrical, Transformation](u, v, z, c)
Мы вычисляем градиент функционального f (u, v, w) = x (u, v, w) в эллиптических цилиндрических координатах
.
f:= (c*cos(v)*cosh(u))^2:
Для вычисления компонентов градиента относительно ортогональной системы достаточно знать 'масштабные коэффициенты':
linalg::ogCoordTab[EllipticCylindrical, Scales](u, v, w, c)
gradf := gradient(f, [u, v, w], %)
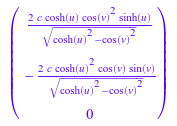
Это коэффициенты градиента относительно ортонормированного базиса
, возвращенного с помощью опции UnitVectors:
[e_u, e_v, e_w] := linalg::ogCoordTab[EllipticCylindrical, UnitVectors](u, v, w, c)
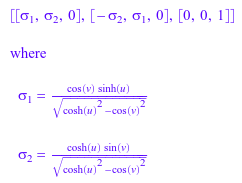
Мы преобразуем списки e_u, e_v, e_w в вектор-столбцы через matrix. Таким образом, в стандартном основании ℝ3, векторное поле градиента:
G := gradf[1]*matrix(e_u)
+ gradf[2]*matrix(e_v)
+ gradf[3]*matrix(e_w)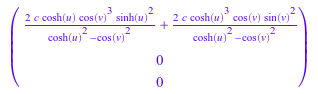
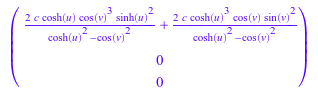
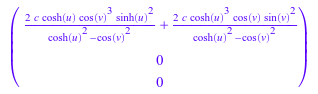
Мы упрощаем это выражение с помощью тождеств sin 2 (v) = 1 - cos 2 (v), sinh 2 (u) = cosh 2 (u) - 1:
normal(subs(G, sin(v)^2 = 1 - cos(v)^2,
sinh(u)^2 = cosh(u)^2 - 1))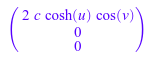
Это - градиент функционального f (x, y, z) = x 2 с x, выраженным эллиптическими цилиндрическими координатами:
G := gradient(x^2, [x, y, z])
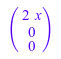
[x, y, z] := linalg::ogCoordTab[EllipticCylindrical, Transformation](u, v, w, c)
map(G, eval)
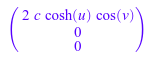
delete f, gradf, e_u, e_v, e_w, G, x, y, z:
|
Имя предопределенной системы координат. Следующие системы трехмерной координаты доступны: |
|
Координаты ортогональной системы: идентификаторы, индексированные идентификаторы или арифметические выражения. |
|
Декартовы координаты: идентификаторы, индексированные идентификаторы или арифметические выражения. |
|
Арифметическое выражение. Значением по умолчанию является |
|
|
|
|
|
|
|
|
Большинство записей в linalg::ogCoordTab функции:
linalg::ogCoordTab [ogName, Transformation]( u1, u2, u3, c ) возвращает список арифметических выражений [ x1( u1, u2, u3), x2( u1, u2, u3), x3( u1, u2, u3)] определение преобразования от прямоугольных координат u i к Декартовым координатам x j.
linalg::ogCoordTab [ogName, InverseTransformation]( x1, x2, x3, c ) возвращает список арифметических выражений [ u1( x1, x2, x3), u2( x1, x2, x3), u3( x1, x2, x3)] определение обратного преобразования.
linalg::ogCoordTab [ogName, UnitVectors]( u1, u2, u3, c ) возвращает список ортогонального модуля “векторы”. “Векторы” даны как списки арифметических выражений.
linalg::ogCoordTab [ogName, Scales]( u1, u2, u3, c ) возвращает список арифметических выражений.
linalg::ogCoordTab [ogName, Ranges]( c ) возвращает список областей значений [ a1.. b1, a2.. b2, a3.. b3]. Преобразование является обратимым для значений параметров a i <u i <b i.
linalg::ogCoordTab [ogName, Dimension] дает к размерности пробела, параметризованного прямоугольными координатами. В настоящее время все предопределенные системы параметризуют ℝ 3, т.е. размерность 3 во всех случаях.
Вызов linalg::ogCoordTab [ogName]( u1, u2, u3, c ) идентично вызову linalg::ogCoordTab [ogName, UnitVectors]( u1, u2, u3, c ).
