linalg::companion
Сопровождающая матрица одномерного полинома
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Синтаксис
linalg::companion(p, <x>)
Описание
linalg::companion(p) возвращает сопровождающую матрицу, сопоставленную с полиномиальным p.
p должен быть monic и степени один, по крайней мере.
Если p полином, т.е. объект типа DOM_POLY, затем определение x не оказывает влияния.
Если p полином, затем звонок компонента возвращенной матрицы является содействующим звонком p, кроме двух случаев для встроенных содействующих звонков: если содействующий звонок p Expr затем доменный Dom::ExpressionField() звонок компонента сопровождающей матрицы. Если это - IntMod(m) затем сопровождающая матрица задана по кольцевому Dom::IntegerMod(m) (см. Пример 2).
Если p многочленное выражение, затем сопровождающая матрица задана по Dom::ExpressionField().
Если p многочленное выражение, содержащее несколько символьных indeterminates затем x должен быть задан и отличает неопределенный x от других символьных параметров.
Примеры
Пример 1
Мы запускаем со следующего многочленного выражения:
delete a_0, a_1, a_2, a_3: p := x^4 + a_3*x^3 + a_2*x^2 + a_1*x + a_0
Чтобы вычислить сопровождающую матрицу p относительно x, мы должны задать второй параметр x, потому что выражение p содержит indeterminates a 0, a 1, a 2, a 3 и x:
linalg::companion(p)
Error: Variables in multivariate polynomials must be specified by the second argument. [linalg::companion]
linalg::companion(p, x)
Конечно, мы можем вычислить сопровождающую матрицу p относительно a 0 также.
linalg::companion(p, a_0)
Следующие сбои с сообщением об ошибке, потому что полиномиальный p не является monic относительно a 1:
linalg::companion(p, a_1)
Error: Polynomial must be monic. [linalg::companion]
Пример 2
Если мы вводим полином по встроенной содействующей области Expr, затем сопровождающая матрица задана по стандартному звонку компонента для матриц (доменный Dom::ExpressionField()):
C := linalg::companion(poly(x^2 + 10*x + PI, [x]))
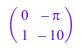
domtype(C)
Если мы задаем полином по сборке - в содействующей области IntMod(m), затем сопровождающая матрица задана по соответствующему кольцевому Dom::IntegerMod(m) компонента, как показано в следующем примере:
p := poly(x^2 + 10*x + 7, [x], IntMod(3))
C := linalg::companion(p)
domtype(C)
Параметры
|
Одномерный полином или многочленное выражение |
|
Возвращаемые значения
Матрица доменного Dom::Matrix(R).
Алгоритмы
Сопровождающая матрица полиномиального x n + a n 1 xn - 1 + … + a 1 x + a 0 является матрицей:
.
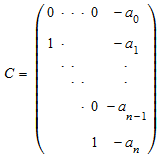Сопровождающая матрица одномерного полиномиального p степени, n является n ×n матричный C с p C = p, где p C является характеристическим полиномом C.