linalg::inverseLUВычисление инверсии матрицы с помощью LU-разложения
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
linalg::inverseLU(A) linalg::inverseLU(L,U,pivindex)
linalg::inverseLU(A) вычисляет инверсию
квадратной матрицы A с помощью LU-разложения.
linalg::inverseLU(L, U, pivindex) вычисляет инверсию матричного A = P - 1 L U где LU и pivindex результат LU-deomposition (несингулярной) Матрицы A, как вычислено linalg::factorLU.
Матричный A должно быть несингулярным.
pivindex список [r[1], r[2], ...] представление матрицы перестановок P, таким образом, что B = PA = LU, где b ij = a r i, j.
Это не проверяется ли pivindex имеет такую форму.
Звонок компонента входных матриц должен быть полем, т.е. областью категории Cat::Field.
Мы вычисляем инверсию матрицы:
A := Dom::Matrix(Dom::Real)( [[2, -3, -1], [1, 1, -1], [0, 1, -1]] )
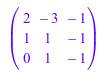
использование LU-разложения:
Ai := linalg::inverseLU(A)
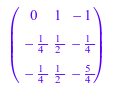
Мы проверяем результат:
A * Ai, Ai * A
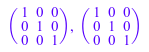
Мы можем также вычислить инверсию A обычным способом:
1/A
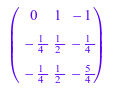
linalg::inverseLU должен использоваться по причинам КПД в случае, где LU-разложение матрицы уже вычисляется, когда следующий пример иллюстрирует.
Если у нас уже есть LU-разложение (несингулярной) матрицы, мы можем вычислить инверсию матричного A = P - 1 L U можно следующим образом:
LU := linalg::factorLU(linalg::hilbert(3))
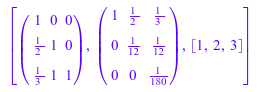
linalg::inverseLU(op(LU))
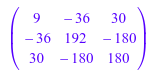
linalg::inverseLU затем только потребности выполнить вперед и обратная подстановка, чтобы вычислить обратную матрицу (см. также linalg::matlinsolveLU).
|
Квадратная матрица области категории |
|
Список положительных целых чисел |
Матрица того же доменного типа как A или L, соответственно.