linalg::minpolyМинимальный полином матрицы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
linalg::minpoly(A, x)
linalg::minpoly(A, x) вычисляет минимальный полином квадратной матрицы A в x, т.е. многочлен самой низкой степени, уничтожающей матричный A.
Минимальный полином A делит характеристический полином A, теоремой Кэли-Гамильтона.
Если матрица задана по Dom::Float, затем из-за числовых ошибок вычисленный полином может иметь степень выше, чем размерность матрицы. В таких случаях, linalg::minpoly возвращает значение FAIL. Смотрите пример 3.
Звонок компонента A должно быть поле, т.е. область категории Cat::Field.
Мы задаем следующую матрицу по рациональным числам:
A := Dom::Matrix(Dom::Rational)( [[0, 2, 0], [0, 0, 2], [2, 0, 0]] )
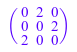
Минимальным полиномом матричного A в переменной x затем дают:
delete x: linalg::minpoly(A, x)
![]()
В этом случае минимальный полином на самом деле равен характеристическому полиному A:
linalg::charpoly(A, x)
![]()
Минимальный полином матрицы:
B := matrix([[0, 1, 0], [0, 0, 0], [0, 0, 0]])
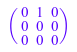
полином степени 2:
m := linalg::minpoly(B, x)
![]()
Характеристический полином B имеет степень 3 и разделен на минимальный полином B:
p := linalg::charpoly(B, x)
![]()
p / m
![]()
Для следующего примера MuPAD® не может вычислить минимальный полином, и таким образом FAIL возвращен:
C := Dom::Matrix(Dom::Float)([ [7, 0, 0, 0, 0], [1, 0, 0, 0, 0], [1, 2, 0, 0, 0], [1, 2, 3, 0, 0], [1, 2, 3, 4, 7] ])

delete x: linalg::minpoly(C, x)
Warning: Unable to compute minimal polynomial. [linalg::minpoly]
![]()
На самом деле для этого примера MuPAD не может проверять на нулевую эквивалентность во время Исключения Гаусса и поэтому выбрал неправильный элемент центра.
Если вы выполняете расчет по коэффициенту domainDom::ExpressionField(normal) вместо этого, затем в большинстве случаев минимальный полином может быть вычислен:
C := matrix([ [7, 0, 0, 0, 0], [1, 0, 0, 0, 0], [1, 2, 0, 0, 0], [1, 2, 3, 0, 0], [1, 2, 3, 4, 7] ])

linalg::minpoly(C, x)
![]()
Однако в целом этой проблемы относительно нулевого распознавания нельзя избежать.
|
Квадратная матрица области категории |
|
Неопределенное |
Полином доменного Dom::DistributedPolynomial([x],R), где R звонок компонента A, или значение FAIL.