linalg::orthogОртогонализация векторов
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
linalg::orthog(S, <Real>)
linalg::orthog(S) ортогонализирует векторы в S с помощью алгоритма Ортогонализации Грама-Шмидта.
Векторы в S ортогонализируются относительно скалярного произведения linalg::scalarProduct.
Если O является возвращенным набором, то векторы O охватывают то же подпространство как векторы в S, и они являются попарно ортогональными, т.е.:![]() для всех
для всех![]() с
с![]() .
.
Возвращенные векторы не нормированы. Чтобы нормировать их используют map(O, linalg::normalize).
Для упорядоченного множества ортогональных векторов, S должен быть список.
Векторы в S должен быть задан по тому же звонку компонента.
Звонок компонента векторов в S должно быть поле, т.е. область категории Cat::Field.
Если вы используете Real опция, linalg::orthog вычисляет ортогональное основание с помощью действительного скалярного произведения в процессе ортогонализации.
Следующий список векторов является основанием векторного пространства ℝ 3:
MatR := Dom::Matrix(Dom::Real): S := [MatR([2, 1, 0]), MatR([-3, 1, 1]), MatR([-1, -1, -1])]
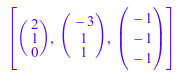
Алгоритм Грама-Шмидта затем возвращает ортогональное основание для ℝ 3. Мы получаем ортонормированный базис со следующим входом:
ON:= linalg::orthog(S)
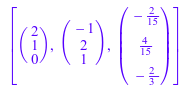
Векторы могут быть нормированы с помощью linalg::normalize:
map(ON, linalg::normalize)
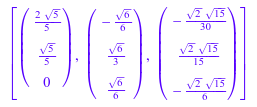
Мы можем также создать матрицу из векторов в S применять linalg::orthog к этой матрице. Результатом является матрица, столбцы которой даны вышеупомянутыми элементами списка ON:
A:= S[1].S[2].S[3]
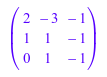
linalg::orthog(A)
Ортогонализация векторов:
T := {matrix([[-2, 5, 3]]), matrix([[0, 2, 1]])}![]()
дает:
linalg::orthog(T)
![]()
Результат linalg::orthog список или набор линейно независимых векторов, даже если вход содержит линейно зависимые векторы:
MatQ := Dom::Matrix(Dom::Rational): S := [MatQ([2, 1]), MatQ([3, 4]), MatQ([-1, 1])]
![]()
linalg::orthog(S)
![]()
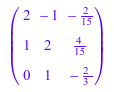
Вычислите ортогональное основание этой матрицы:
A := matrix([[a, 1], [1, a]]): linalg::orthog(A)
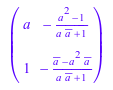
Чтобы избежать сопряженных комплексных чисел, используйте Real опция:
linalg::orthog(A, Real)
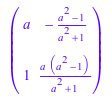
|
Набор или список векторов той же размерности (вектором является n ×1 или 1 ×n матрица области категории |
|
Избегайте использования комплексного скалярного произведения в процессе ортогонализации. |
Установите или список векторов, соответственно.