Взаимодействия среды

Свойства идентификаторов учтены.

Пример 1

Мы вычисляем скалярное произведение векторов (i, 1) и (1, - i):

MatC := Dom::Matrix(Dom::Complex):
u := MatC([I, 1]): v := MatC([1, -I]):
linalg::scalarProduct(u, v)

Пример 2

Мы вычисляем скалярное произведение векторов и с символьными записями u ₁, u ₂, v ₁, v ₂ по стандартному звонку компонента для матриц:

delete u1, u2, v1, v2:
u := matrix([u1, u2]): v := matrix([v1, v2]):
linalg::scalarProduct(u, v)

Можно использовать assume чтобы сказать систему, что символьные компоненты должны представлять вещественные числа:

assume([u1, u2, v1, v2], Type::Real):

Затем скалярное произведение и упрощает до:

linalg::scalarProduct(u, v)

В качестве альтернативы опция Real может быть задан:

unassume(u1, u2, v1, v2):
linalg::scalarProduct(u, v, Real)

Пример 3

Одно конкретное скалярное произведение в вещественном векторном пространстве непрерывных функций на интервале [0, 1] задано

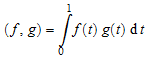Чтобы вычислить ортогональное основание, соответствующее полиномиальному основанию 1, t, t ², t ³, … относительно этого скалярного произведения, мы заменяем стандартное скалярное произведение следующей процедурой:

standardScalarProduct := linalg::scalarProduct:
unprotect(linalg):
linalg::scalarProduct := proc(u, v) 
    local F, f, t;
begin
    // (0)
    f := expr(u[1] * v[1]);

     // (1)
    t := indets(f);
    if t = {} then t := genident("t") else t := op(t, 1) end_if;

     // (2)
    F := int(f, t = 0..1);

     // (3)
    u::dom::coeffRing::coerce(F)
end:

Мы запускаем с шага (0) преобразовывать f (t)  g (t) к выражению основного доменного типа, такого что системная функция int на шаге (2) может обработать его вход (это не необходимо, если элементы звонка компонента векторов уже представлены элементами основных областей).

Шаг 1 извлекает неопределенные из полиномов, шаг (2) вычисляет скалярное произведение, как задано выше и шаг (3) преобразует результат назад в элемент звонка компонента векторов u и v.

Обратите внимание на то, что мы должны оставить идентификатор, защищенный от записи без защиты, linalg, в противном случае присвоение привело бы к сообщению об ошибке.

Мы затем создаем матрицу, которая состоит из первых пяти из вышеупомянутых полиномов:

P := matrix([[1, t, t^2, t^3, t^4]])

Если мы теперь выполняем процедуру Ортогонализации Грама-Шмидта на столбцах P с функциональным linalg::orthog, мы добираемся:

S := linalg::orthog(linalg::col(P, 1..4))

Каждый вектор в S является ортогональным к другим векторам в S относительно модифицированного скалярного произведения. Мы проверяем это на первый вектор:

linalg::scalarProduct(S[1], S[j]) $ j = 2..nops(S)

Наконец, мы отменяем переопределение скалярного произведения, чтобы не столкнуться с проблемой с последующими расчетами:

linalg::scalarProduct := standardScalarProduct:
protect(linalg, Error):

Возвращаемые значения

Элемент звонка компонента u и v.