linalg::rankРанг матрицы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
linalg::rank(A) linalg::rank(S)
linalg::rank(A) вычисляет ранг матричного A.
linalg::rank(S) вычисляет ранг матрицы, столбцы которой являются векторами в S.
Ранг строки матрицы является максимальным количеством линейно независимых векторов-строк из той матрицы. Ранг столбца матрицы является максимальным количеством линейно независимых вектор-столбцов той матрицы. Для каждой матрицы ее ранг строки равен ее рангу столбца. Этот номер называется рангом матрицы.
Звонок компонента A или векторов, данных в S должна быть интегральная область (область категории Cat::IntegralDomain).
linalg::rank заменяет символьные элементы матрицы случайными целыми числами между 1 и 1010. Затем функция вычисляет ранг получившейся числовой матрицы Исключением Гаусса (см. linalg::gaussElim). Этот подход вводит крошечный шанс получения неправильного результата.
linalg::rank не упрощает специальные функции и алгебраические числа. Для некоторых матриц этот подход приводит к неправильным результатам. Смотрите Пример 3.
Задайте следующий матричный A по ℤ:
MatZ := Dom::Matrix(Dom::Integer): A := MatZ([[1, 2, 3, 4], [-1, 0, 1, 0], [3, 5, 6, 9]])

Вычислите ранг матричного A:
linalg::rank(A)
![]()
Используйте эти три вектора![]() , чтобы задать столбцы матричного
, чтобы задать столбцы матричного A. Вычислите ранг A:
MatZ := Dom::Matrix(Dom::Integer):
S:= { MatZ([0,1,1]), MatZ([0,1,0]), MatZ([0,0,1]) }:
linalg::rank(S)![]()
linalg::rank функция не использует правил упрощения для специальных функций, алгебраические числа (радикалы), и так далее. Если linalg::rank вычисляет промежуточные выражения, которые могут быть упрощены до нуля, функция может возвратить неправильные результаты. Например, создайте следующие матрицы:
A := matrix([[exp(x + y), exp(x)], [exp(y), 1]]); B := matrix([[sin(x)^2 + cos(x)^2, 1], [1, 1]]); C := matrix([[sqrt(6), sqrt(2)], [sqrt(3), 1]])
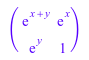
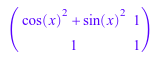
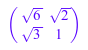
Существует только одна независимая строка в каждой из этих матриц. Ранг матриц AB, и C 1. linalg::rank функция возвращается 2, потому что она не упрощает выражения![]() , sin 2 + cos 2 - 1, и
, sin 2 + cos 2 - 1, и![]() :
:
linalg::rank(A), linalg::rank(B), linalg::rank(C)
![]()
|
Матрица A области категории |
|
Список или набор вектор-столбцов той же размерности (вектор-столбцом является n ×1 матрица области категории |
Неотрицательное целое число