linalg::sqrtMatrixКвадратный корень из матрицы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
linalg::sqrtMatrix(A, <sqrtfunc>)
linalg::sqrtMatrix(A) возвращает квадратный корень из матричного A.
Квадратный корень из диагональной матрицы дан диагональной матрицей, диагональные элементы которой являются только квадратными корнями из исходной матрицы.
Вычислите квадратный корень из матрицы
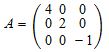 :
:
A := matrix([[4, 0, 0], [0, 2, 0], [0, 0, -1]]): S := linalg::sqrtMatrix(A)
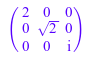
Проверяйте правильность результата:
S^2

Вычислите квадратный корень из матрицы
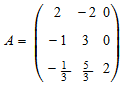 :
:
A := matrix([[2, -2, 0], [-1, 3, 0], [-1/3, 5/3, 2]]): S := linalg::sqrtMatrix(A)
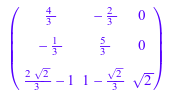
Если вы вычисляете квадрат матричного S и упростите результат, вы получаете матричный A:
simplify(S^2)
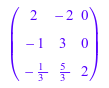
Используя функциональный x -> -sqrt(x) в качестве второго аргумента для расчета квадратного корня из матричного A, получите различную матрицу, компоненты которой являются только отрицательными компонентами исходного квадратного корня, вычисленного выше:
S:= linalg::sqrtMatrix(A, x -> -sqrt(x)): S, simplify(S^2);
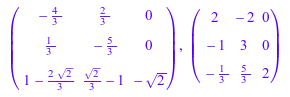
|
Квадратная матрица области категории |
|
Функция, удовлетворяющая sqrtfunc (a) 2 = a для каждого элемента a содействующего звонка A (т.е. функция квадратного корня содействующей области A). |
Матричный B с B 2 = A, таким образом, что собственные значения B являются квадратными корнями из собственных значений A или FAIL если квадратный корень из матрицы не существует