linalg::eigenvectorsСобственные вектора матрицы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
linalg::eigenvectors(A)
linalg::eigenvectors(A) вычисляет собственные значения и собственные вектора матричного A.
Приближение с плавающей точкой собственных значений и собственных векторов вычисляется с помощью numeric::eigenvectors, если матричный A задан по кольцевому Dom::Float компонента (см. Пример 1). В этом случае рекомендуется вызвать numeric::eigenvalues непосредственно для лучшего КПД.
linalg::eigenvectors работает можно следующим образом: Для каждого собственного значения λ n ×n матричный A, основание для ядра (λ In - A), eigenspace A относительно собственного значения λ, вычисляется с помощью Алгоритма Гаусса-Жордана (см. linalg::gaussJordan). Здесь, I n обозначает n ×n единичная матрица.
Собственные вектора имеют доменный Dom::Matrix(R), где R звонок компонента A.
Звонок компонента матричного A должно быть поле, т.е. область категории Cat::Field, для которого решатель solve может вычислить нули полинома.
Это может произойти что основание для eigenspace A относительно определенного собственного значения не может быть вычислен (например, если звонок компонента не имеет канонического представления нулевого элемента). В этом случае linalg::eigenvectors ответы с предупреждающим сообщением и возвращают FAIL.
Мы вычисляем собственные значения и собственные вектора матрицы
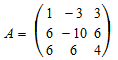 :
:
A := Dom::Matrix(Dom::Rational)( [[1, -3, 3], [6, -10, 6], [6, 6, 4]] ): Ev:= linalg::eigenvectors(A)
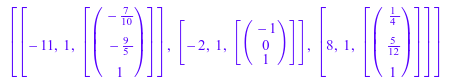
Матричный A является диагонализируемым. Следовательно, мы извлекаем собственные вектора и комбинируем их к матричному P таким образом, что P^-1 * A * P диагональная матрица, диагональные элементы которой даны соответствующими собственными значениями:
Eigenvectors:= Ev[1][3][1], Ev[2][3][1], Ev[3][3][1]
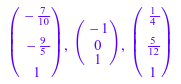
P:= Eigenvectors[1].Eigenvectors[2].Eigenvectors[3]
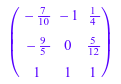
P^-1 * A * P

Более квалифицированный способ извлечь вышеупомянутые собственные вектора из выхода сгенерирован linalg::eigenvectors следующее:
map(Ev, op@op, 3)
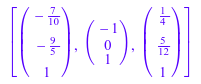
Если мы рассматриваем матричный A по доменному Dom::Float, вызов linalg::eigenvectors(A) результаты в численном расчете собственных значений и собственных векторах A через функциональный numeric::eigenvectors:
B := Dom::Matrix(Dom::Float)(A): linalg::eigenvectors(B)

|
Квадратная матрица области категории |
Список подсписков, где каждый подсписок состоит из собственного значения λ A, его алгебраическая кратность и основание для eigenspace λ. Если основание eigenspace не может быть вычислено, FAIL возвращен.