numeric::eigenvectorsЧисловые собственные значения и собственные вектора матрицы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
numeric::eigenvectors(A, options)
numeric::eigenvectors(A) возвращает числовые собственные значения и собственные вектора матричного A.
Все записи матрицы должны быть числовыми. Числовые выражения такой как![]() и т.д. приняты и преобразованы в плавания. Нечисловые символьные записи приводят к ошибке.
и т.д. приняты и преобразованы в плавания. Нечисловые символьные записи приводят к ошибке.
Собственные значения сортируются по numeric::sort.
Матричный X обеспечивает собственные вектора: i-th столбец X числовой собственный вектор, соответствующий собственному значению di. Каждый столбец является или нулем или нормированный к Евклидовой длине 1.0.
Для матриц с несколькими собственными значениями и недостаточным количеством собственных векторов, некоторые собственные вектора могут совпасть или могут быть нулем, т.е. X является не обязательно обратимым.
Список остатков res = [res 1, res 2, …] обеспечивает некоторое управление качеством числовых спектральных данных. Остатками дают
![]() ,
,
где x i является нормированным собственным вектором (i-th столбец X) сопоставленный с числовым собственным значением d i. Для Эрмитовых матриц res i обеспечивает верхнюю границу для абсолютной погрешности d i.
С опцией NoResidues, расчет остатков подавлен, возвращенным значением является NIL.
Если никакие не возвращаются, тип задан с помощью опции ReturnType = t, доменный тип матрицы собственного вектора X зависит от типа входной матрицы A:
Собственные вектора плотной матрицы типа Dom::DenseMatrix() возвращены как плотная матрица типа Dom::DenseMatrix() по звонку выражений.
Для всех других матриц категории Cat::Matrix, собственные вектора возвращены как матрицы типа Dom::Matrix() по звонку выражений MuPAD®. Это включает входные матрицы A из типа Dom::Matrix(...), Dom::SquareMatrix(...), Dom::MatrixGroup(...) и т.д.
Матрицы A из матричной области, такой как Dom::Matrix(...) или Dom::SquareMatrix(...) внутренне преобразованы в массивы по выражениям через expr(A). Обратите внимание на то, что linalg::eigenvectors должен использоваться, когда собственные значения/векторы должны быть вычислены по области компонента. См. Пример 3.
Собственные значения аппроксимированы абсолютной точностью![]() , где r является спектральным радиусом
, где r является спектральным радиусом A (т.е. r является максимальным сингулярным значением A). Следовательно, большие собственные значения должны быть вычислены правильно к DIGITS десятичные разряды. Числовые приближения маленьких собственных значений менее точны.
Для числового алгоритма не возможно различать плохо разделенные отличные собственные значения и несколько собственных значений. Поэтому numeric::eigenvectors и linalg::eigenvectors использование различные форматы возврата: последний может предоставить информацию о кратности собственных значений из-за ее внутренней точной арифметики.
Используйте numeric::eigenvalues если только собственные значения должны быть вычислены.
Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы вычисляем спектральные данные 2×2 Гильбертова матрица:
A := linalg::hilbert(2)
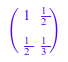
[d, X, res] := numeric::eigenvectors(A):
Собственные значения:
d
![]()
Собственные вектора:
X
![]()
Гильбертовы матрицы являются Эрмитовыми, т.е. вычисление спектральных данных является численно устойчивым процессом. Это подтверждено маленькими остатками:
res
![]()
Стандартный linalg::hilbert обеспечивает вход как матрицу типа Dom::Matrix(). Следовательно, собственные вектора также состоят из такой матрицы. Для последующей обработки мы преобразуем список собственных значений к диагональной матрице:
d := matrix(2, 2, d, Diagonal):
Мы восстанавливаем матрицу из ее спектральных данных:
X*d*X^(-1)
![]()
Мы извлекаем собственный вектор из матричного X и перепроверьте его числовое качество:
eigenvector1 := X::dom::col(X, 1); norm(A*eigenvector1 - d[1, 1]*eigenvector1)
![]()
![]()
delete A, d, X, res, eigenvector1:
Мы демонстрируем численно плохо обусловленный случай. Следующая матрица имеет только один собственный вектор и не может быть diagonalized. Численно, нулевой вектор возвращен как второй столбец матрицы собственного вектора:
A := array(1..2, 1..2, [[5, -1], [4, 1]]): DIGITS := 6: numeric::eigenvectors(A)
![]()
delete A, DIGITS:
Следующая матрица имеет доменные компоненты:
A := Dom::Matrix(Dom::IntegerMod(7))([[6, -1], [0, 3]])

Обратите внимание на то, что numeric::eigenvectors вычисляет спектральные данные следующей матрицы:
expr(A)
![]()
numeric::eigenvectors(A, NoResidues)
![]()
Стандартный linalg::eigenvectors должен использоваться, если спектральные данные должны быть вычислены по доменному Dom::IntegerMod компонента(7):
linalg::eigenvectors(A)
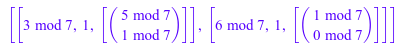
delete A:
Мы демонстрируем использование аппаратных плаваний. Следующая матрица является вырожденной: это имеет ранг 1. Для двойного собственного значения 0, различные основные векторы соответствующего eigenspace возвращены с HardwareFloats и SoftwareFloats, соответственно:
A := array(1..3, 1..3, [[1, 2, 3], [2, 4, 6],
[3*10^12, 6*10^12, 9*10^12]]):
[d1, X1, res1] := numeric::eigenvectors(A, HardwareFloats):
d1, X1
[d2, X2, res2] := numeric::eigenvectors(A, SoftwareFloats): d2, X2
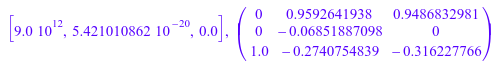
delete A, d1, X1, res1, d2, X2, res2:
|
Числовая матрица доменный тип |
|
С С По сравнению с Если никакой Если результат не может быть вычислен с аппаратными плаваниями, арифметику программного обеспечения ядром MuPAD пробуют. Если текущее значение Может быть несколько причин аппаратной арифметики, чтобы перестать работать:
Если никакой Если Обратите внимание на то, что Запаздывающие цифры в результатах с плавающей точкой вычисляются с ПримечаниеДля плохих обусловленных матриц результаты, возвращенные с |
|
Подавляет расчет ошибочных оценок Если никакие ошибочные оценки не требуются, эта опция может использоваться, чтобы подавить расчет остатков Альтернативная опция называет |
|
Опция, заданная как Возвратите собственные вектора как матрицу доменного типа |
|
Отключает предупреждения |
Перечислите [d, X, res]. Список d = [d1, d2, …] содержит числовое собственное значение. i-th столбец матричного X собственный вектор, сопоставленный с собственным значением di. Список остатков res = [res1, res2, …] обеспечивает ошибочные оценки для числовых собственных значений.
Стандартная программа реализует стандартные числовые алгоритмы из Руководства Автоматического Расчета Уилкинсоном и Рейншем.