numeric::eigenvaluesЧисловые собственные значения матрицы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
numeric::eigenvalues(A, options)
numeric::eigenvalues(A) возвращает числовые собственные значения матричного A.
Все записи A должно быть числовым. Числовые выражения такой как
и т.д. приняты и преобразованы в плавания. Нечисловые символьные записи приводят к ошибке.
Матрицы A из матричной области, такой как Dom::Matrix(...) или Dom::SquareMatrix(..) внутренне преобразованы в массивы по выражениям через expr(A). Обратите внимание на то, что linalg::eigenvalues должен использоваться, когда собственные значения должны быть вычислены по области компонента. См. Пример 2.
Собственные значения сортируются по numeric::sort.
Собственные значения аппроксимированы абсолютной точностью
, где r является спектральным радиусом A (т.е. r является максимумом абсолютных значений собственных значений). Следовательно, большие собственные значения должны быть вычислены правильно к DIGITS десятичные разряды. Числовые приближения маленьких собственных значений менее точны.
Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы вычисляем собственные значения 3×3 Гильбертова матрица:
numeric::eigenvalues(linalg::hilbert(3))
Следующая матрица плохо обусловлена. Это имеет очень большие, а также очень маленькие собственные значения:
A := array(1..3, 1..3,
[[ I , PI , exp(1) ],
[ 2 , 10^100 , 1 ],
[10^(-100), 10^(-100), 10^(-100)]
]):Цель точности и рабочая точность установлены DIGITS. Со стандартной настройкой DIGITS = 10, следующий результат вычисляется с HardwareFloats:
numeric::eigenvalues(A)
Обратите внимание на то, что маленькие собственные значения могут быть под влиянием округления. Мы увеличиваем рабочую точность путем увеличения DIGITS. Самое маленькое из собственных значений вычисляется более точно:
DIGITS := 200: eigenvals := numeric::eigenvalues(A): DIGITS := 5: eigenvals;
delete A, eigenvals, DIGITS:
Следующая матрица имеет доменные компоненты:
A := Dom::Matrix(Dom::IntegerMod(7))(
[[6, -1, 4], [0, 3, 3], [0, 0, 3]])
Обратите внимание на то, что numeric::eigenvalues вычисляет собственные значения следующей матрицы:
expr(A), numeric::eigenvalues(A)
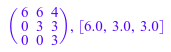
Если собственные значения должны быть вычислены по доменному Dom::IntegerMod(7) компонента, linalg::eigenvalues должен использоваться:
linalg::eigenvalues(A, Multiple)
delete A:
Мы демонстрируем использование аппаратных плаваний. Гильбертовы матрицы известно плохо обусловлены: расчет маленьких собственных значений подвергается серьезным эффектам округления. В следующих результатах, обоих с HardwareFloats а также с SoftwareFloats, маленькие собственные значения омрачены числовым округлением:
A := linalg::hilbert(15): numeric::eigenvalues(A, HardwareFloats), numeric::eigenvalues(A, SoftwareFloats)
delete A:
|
Числовая матрица доменный тип |
|
С С По сравнению с Если никакой Если результат не может быть вычислен с аппаратными плаваниями, арифметику программного обеспечения ядром MuPAD пробуют. Если текущее значение Может быть несколько причин аппаратной арифметики, чтобы перестать работать:
Если никакой Если Обратите внимание на то, что Запаздывающие цифры в результатах с плавающей точкой вычисляются с ПримечаниеДля плохих обусловленных матриц результаты, возвращенные с |
|
Отключает предупреждения |
Упорядоченный список числовых собственных значений
Функция реализует стандартные числовые алгоритмы из Руководства Автоматического Расчета Уилкинсоном и Рейншем.