ParameterName, ParameterBegin, ParameterEnd, ParameterRangeИмя параметра анимации
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
ParameterBegin, ParameterEnd'ParameterName' | Дополнительный | Выражение MuPAD® |
ParameterRange | [ParameterBegin .. ParameterEnd] | Область значений из арифметических выражений |
Как правило, анимации инициированы путем передачи уравнения формы a = `a_{min}`..`a_{max}` в определении объекта.
Это эквивалентно передаче атрибутов ParameterName = a, ParameterBegin = amin, и ParameterEnd = amax в определении объекта.
Атрибут ParamterRange = `a_{min}`..`a_{max}` эквивалентно установке обоих ParameterBegin = amin и ParameterEnd = amax.
Анимации заданы объект объектом, не структурируют системой координат.
В большинстве случаев пользователь задаст анимации путем передачи уравнения формы a = `a_{min}`..`a_{max}` в определении объекта. Любое уравнение этой формы, которая не важна для определения статической версии объекта, интерпретировано как параметр анимации и область значений анимации.
Передача такого уравнения эквивалентна установке трех атрибутов
ParameterName = a, ParameterBegin = amin, ParameterEnd = amax.
Атрибут ParamterRange = `a_{min}`..`a_{max}` служит коротким путем для установки обоих ParameterBegin = amin и ParameterEnd = amax.
Значения amin и amax значения параметров вначале и конец оперативной области значений, в которой анимирован объект. На этот раз область значений установлена атрибутами TimeBegin и TimeEnd, соответственно.
Область значений параметра `a_{min}`..`a_{max}` сопоставлен линейно с этим временным интервалом.
Имя параметра анимации может быть идентификатором или индексируемым идентификатором. Этот параметр является 'глобальной переменной', которая может присутствовать в других количествах или атрибутах, задающих объект.
Определение объекта может включить процедуры, а не символьные выражения. Например, 2D график функций может быть задан plot::Function2d(f, x = x_0..x_1), где f является процедурой, принимающей один числовой аргумент x из области значений графика между x 0 und x1.
В анимированной версии plot::Function2d(f, x = x_0..x_1, a = `a_{min}`..`a_{max}`), функциональный f будет вызван двумя аргументами x и a. Таким образом f может быть задан как функция, принимающая два параметра x, a или как функция одним параметром x, с помощью параметра анимации a в качестве глобальной переменной.
Каждый анимированный объект имеет свой собственный параметр анимации и область значений `a_{min}`..`a_{max}`. Не необходимо, чтобы несколько анимированных объектов в сцене использовали то же название параметра. Это не используется, чтобы синхронизировать анимации.
Синхронизация определяется исключительно линейным соответствием между областью значений анимации `a_{min}`..`a_{max}` и оперативный промежуток анимации, установленной атрибутами TimeBegin и TimeEnd из объекта.
Определение статического 2D графика функций включает спецификацию одной области значений (для переменной x):
plot(plot::Function2d(sin(x), x = 0 .. 2*PI))
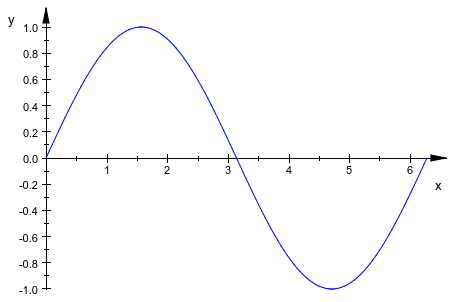
Когда “избыточное уравнение” a = `a_{min}`..`a_{max}` передается, это интерпретировано как вызов, чтобы анимировать функцию. Параметр анимации может подняться в выражении, задающем функцию:
plot(plot::Function2d(sin(x + a), x = a .. 2*PI, a = 0..PI))
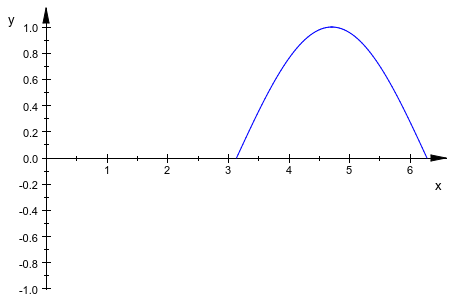
Статический график функций в 3D требует двух областей значений (для x и переменной y):
plot(plot::Function3d(sin(x)*sin(y), x = 0 .. PI, y = 0..PI))
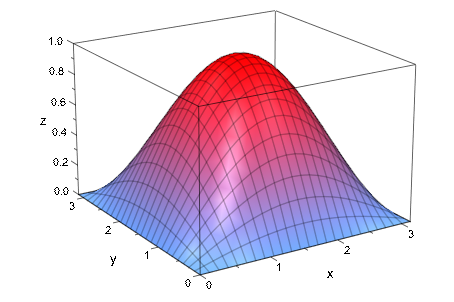
Теперь третье уравнение a = `a_{min}`..`a_{max}` триггеры анимация:
plot(plot::Function3d(sin(x + a)*sin(y - a), x = 0 .. PI,
y = 0..PI, a = 0..PI))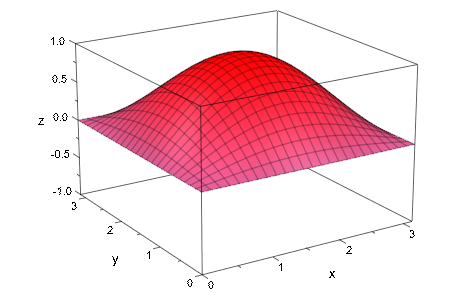
Мы задаем анимированный 2D график функций:
f := plot::Function2d(x^3 + a*x, x = -1..1, a = 0..2): plot(f):
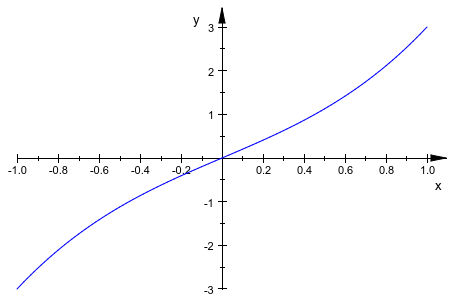
Мы подкачиваем роль независимой переменной x и параметр анимации a:
[f::XName, f::ParameterName] := [f::ParameterName, f::XName]:
[f::XRange, f::ParameterRange] :=
[f::ParameterRange, f::XRange]:Функция теперь чертится как функция a для различных значений “времени” x:
plot(f)
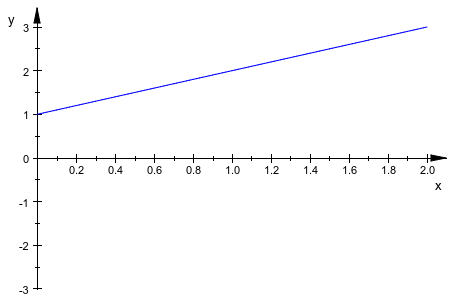
delete f:
Мы демонстрируем использование процедур в определении анимированных функций.
Мы хотим построить собственные значения матрицы, которая зависит от двух параметров x и a. Собственные значения вычисляются численно в процедуре eigenvals. Эта процедура использует option remember, потому что это называется трижды с теми же аргументами процедурами f1, f2, f3 тот продукт самое маленькое, середина и самое большое собственное значение, соответственно, как функции параметров x и a:
eigenvals :=
proc(x, a)
option remember;
local A;
begin
A:= matrix([[1, a, x ],
[a, 2, a*x],
[x, a*x, 3 ]]):
sort(numeric::eigenvalues(A)):
end_proc:
f1:= (x, a) -> eigenvals(x, a)[1]:
f2:= (x, a) -> eigenvals(x, a)[2]:
f3:= (x, a) -> eigenvals(x, a)[3]:plot(plot::Function2d(f1, x = -2..2, a = 0..2,
Color = RGB::Red),
plot::Function2d(f2, x = -2..2, a = 0..2,
Color = RGB::Green),
plot::Function2d(f3, x = -2..2, a = 0..2,
Color = RGB::Blue)):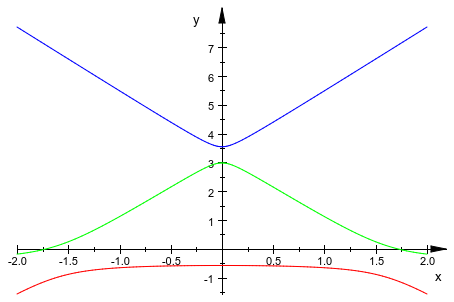
delete eigenvals, f1, f2, f3: