Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Каждый примитив plot библиотека знает, сколько спецификаций типа “располагается”, это должно ожидать. Например, одномерный функциональный график в 2D такой как
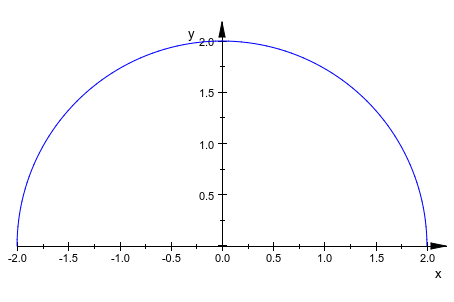
plot::Function2d(sin(x), x = 0..2*PI):
ожидает одну область значений графика для координаты x, тогда как график двумерной функции в 3D ожидает две области значений графика для координаты y и x:
plot::Function3d(sin(x^2 + y^2), x = 0..2, y = 0..2):
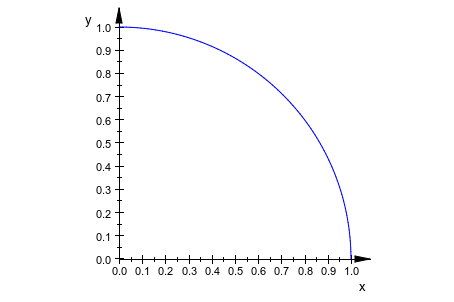
Контурный график в 2D ожидает 2 области значений для координаты y и x:
plot::Implicit2d(x^2 + y^2 - 1, x = -2..2, y = - 2..2):
Контурный график в 3D ожидает 3 области значений для x, y и координаты z:
plot::Implicit3d(x^2 + y^2 + z^2 - 1, x = -2..2,
y = - 2..2, z = - 2..2):Линия в 2D не ожидает спецификации области значений:
plot::Line2d([0, 0], [1, 1]):
Каждый раз, когда графический примитив получает “избыточную” спецификацию области значений уравнением, таким как a = amin..amax, параметр a интерпретирован как “параметр анимации” принятие значений от amin к amax.
Таким образом очень легко действительно создать анимированные объекты: Только передайте “избыточное” уравнение области значений a = amin..amax к генерирующемуся вызову примитива. Будут анимированы все другие записи и атрибуты примитива, которые являются символьными выражениями параметра анимации. В следующем вызове оба выражение function, а также область значений x функционального графика зависит от параметра анимации. Кроме того, области значений, задающие ширину и высоту прямоугольника, а также конечную точку линии, зависят от него:
plot(
plot::Function2d(a*sin(x), x = 0..a*PI, a = 0.5..1),
plot::Rectangle(0..a*PI, 0..a, a = 0.5..1,
LineColor = RGB::Black),
plot::Line2d([0, 0], [PI*a, a], a = 0.5 ..1,
LineColor = RGB::Black)
)
Дополнительные спецификации области значений могут войти через графические атрибуты. Вот анимированная дуга, радиус которой и “угловая область значений” зависит от параметра анимации:
plot(plot::Arc2d(1 + a, [0, 0], AngleRange = 0..a*PI, a = 0..1)):
Здесь, атрибут AngleRange идентифицирован его названием атрибута и таким образом не принят, чтобы быть спецификацией параметра анимации с областью значений анимации.
Действительно убедитесь, что атрибуты заданы их правильными именами. Если неправильное название атрибута используется, оно может быть принято за параметр анимации!
В следующих примерах мы хотим задать статический полукруг, с помощью plot::Arc2d с AngleRange = 0..PI. Однако AngleRange записан неправильно. График создается. Это - анимированный полный круг параметром анимации AngelRange!
plot(plot::Arc2d(1, [0, 0], AngelRange = 0..PI)):
Параметр анимации может быть любым символьным параметром (identifier или indexed identifier) это отличается от символов, используемых в обязательных спецификациях области значений (таких как имена независимых переменных в функциональных графиках). Параметр должен также отличаться от любого из защищенных имен атрибутов графика.
Анимации являются созданным объектом объектом. Имена параметров анимации в различных объектах не должны совпадать.
В следующем примере, различные имена aB используются в параметрах анимации двух функций:
plot(plot::Function2d(4*a*x, x = 0..1, a = 0..1),
plot::Function2d(b*x^2, x = 0..1, b = 1..4)):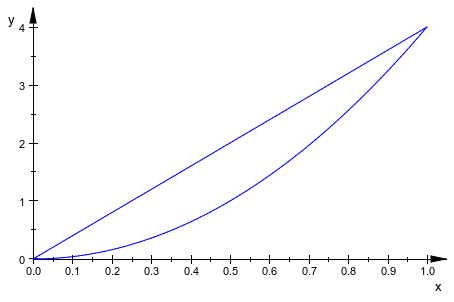
Параметр анимации является глобальным символьным именем. Это может использоваться в качестве глобальной переменной в процедурах, задающих графический объект. Следующий пример показывает 3D график двумерной функции, которая задана процедурой с помощью глобально заданного параметра анимации. Далее, fill color functionmycolor задан, который изменяет цвет в ходе анимации. Это могло использовать параметр анимации в качестве глобального параметра, в качестве функционального f делает. В качестве альтернативы параметр анимации может быть объявлен как дополнительный входной параметр. Обратитесь к странице справки FillColorFunction узнать, сколько ожидают введенные параметры функция цвета заливки и какой из входных параметров питается параметром анимации. Каждый находит это для plot::Function3d, функция цвета заливки вызвана с координатами x, y, z точек на графике. Следующий входной параметр (4-й аргумент mycolor) параметр анимации:
f := (x, y) -> 4 - (x - a)^2 - (y - a)^2:
mycolor := proc(x, y, z, a)
local t;
begin
t := sqrt((x - a)^2 + (y - a)^2):
if t < 0.1 then
return(RGB::Red)
elif t < 0.4 then
return(RGB::Orange)
elif t < 0.7 then
return(RGB::Green)
else return(RGB::Blue)
end_if;
end:
plot(plot::Function3d(f, x = -1..1, y = -1..1, a = -1..1,
FillColorFunction = mycolor)):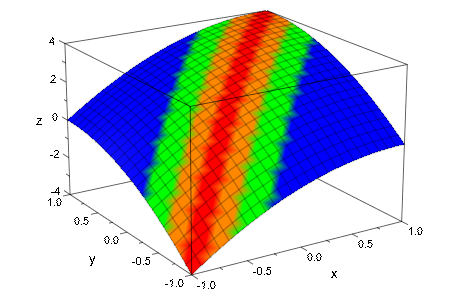
Когда анимированный график создается в блокноте MuPAD®, первая система координат анимации появляется как статическое изображение ниже входной области. Чтобы запустить анимацию, дважды щелкают по графику. Значок для запуска анимации появится (убедитесь, что элемент ‘Панель Анимации’ меню 'View' включен):
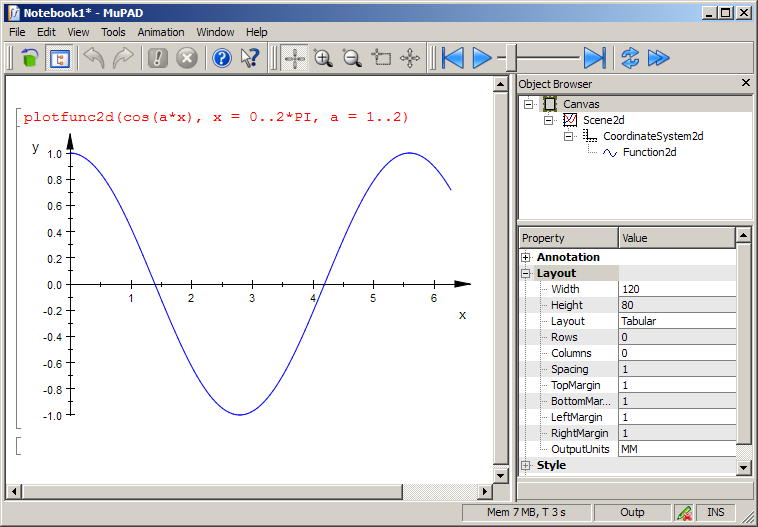
Можно также использовать ползунок, чтобы анимировать изображение “вручную”. В качестве альтернативы меню 'Animation' обеспечивает элемент для запуска анимации.
По умолчанию анимация состоит из 50 различных систем координат. Номер систем координат может быть определен, чтобы быть любым положительным числом n путем определения атрибута Frames = n. Этот атрибут может быть установлен в генерирующемся вызове анимированных примитивов, или в некотором более высоком узле графического дерева. В последнем случае этот атрибут наследован ко всем примитивам, которые существуют ниже узла. С a = amin..amax, Frames = n, i-th система координат состоит из снимка состояния примитива с
![]() .
.
Увеличение числа систем координат не означает, что анимация запускается дольше; средство отображения не работает с постоянным числом кадров в секунду, но обрабатывает все кадры в фиксированном временном интервале.
В фоновом режиме существуют “часы реального времени”, используемые, чтобы синхронизировать анимацию различных анимированных объектов. Анимация имеет область значений времени, измеренную этими часами. Область значений времени установлена атрибутами TimeBegin = t0, TimeEnd = t1 или, эквивалентно, TimeRange = t0..t1, где t0t1 действительные численные значения, представляющие физические времена в секундах. Они приписывают, может быть установлен в генерирующемся вызове анимированных примитивов, или в некотором более высоком узле графического дерева. В последнем случае эти атрибуты наследованы всеми примитивами, которые существуют ниже узла.
Абсолютное значение t0 не важно, если все анимированные объекты совместно используют ту же область значений времени. Только разница во времени t1 - t0 вопросы. Это - (приближение) физическое время в секундах, которые продлится анимация.
Область значений параметра amin..amax в спецификации параметра анимации a = amin..amax вместе с Frames = n задает равноотстоящую mesh времени во временном интервале, установленном TimeBegin = t0 и TimeEnd = t1. Система координат с a = amin отображается в то время t0, система координат с a = amax отображается в то время t1.
С TimeBegin = 0 по умолчанию, значение атрибута TimeEnd дает физическое время анимации в секундах. Значением по умолчанию является TimeEnd = 10, т.е. анимация с помощью значений по умолчанию продлится приблизительно 10 секунд. Номер систем координат определяется Frames = n не влияет на временной интервал, но изменяет количество систем координат, отображенных в этом временном интервале.
Вот простой пример:
plot(plot::Point2d([a, sin(a)], a = 0..2*PI,
Frames = 100, TimeRange = 0..5)):
Точка будет анимирована в течение приблизительно 5 физических секунд, в которые она проходит один период графика синуса. Каждая система координат отображена в течение приблизительно 0,05 секунд. После увеличения числа систем координат фактором 2, каждая система координат отображена в течение приблизительно 0,025 секунд, делая анимацию несколько более сглаженной:
plot(plot::Point2d([a, sin(a)], a = 0..2*PI,
Frames = 200, TimeRange = 0..5)):
Обратите внимание на то, что человеческий глаз не может различать различные системы координат, если они изменяются с уровнем больше чем 25 кадров в секунду. Таким образом количество систем координат набор n для анимации должно удовлетворить
![]() .
.
Следовательно, со временем по умолчанию располагаются TimeBegin = t0 = 0, TimeEnd = t1 = 10 (секунды), это не целесообразно задавать Frames = n с n > 250. Если более высокий номер системы координат требуется, чтобы получать достаточное разрешение анимированного объекта, нужно увеличить время для анимации достаточно высоким значением TimeEnd.
Мы можем рассматривать графический примитив как набор атрибутов графика. (Действительно, также выражение function sin(x) в plot::Function2d(sin(x), x = 0..2*PI) внутренне понят в атрибуте Function = sin(x).) Так, вопрос:
“Какие атрибуты могут быть анимированы?”
Ответ: “Почти любой атрибут может быть анимирован!” Вместо того, чтобы перечислить атрибуты, которые позволяют анимацию, намного легче охарактеризовать атрибуты, которые не могут быть анимированы:
Ни один из canvas атрибуты могут быть анимированы. Это включает параметры размещения, такие как физический размер изображения. Смотрите страницу справки plot::Canvas для полного списка всех атрибутов холста.
Ни один из атрибутов 2D scenes и 3D scenes может быть анимирован. Это включает параметры размещения, цвет фона и стиль, расположение камеры в 3D и т.д. Смотрите страницы справки plot::Scene2d и plot::Scene3d для полного списка всех атрибутов сцены.
Обратите внимание на то, что существуют объекты камеры типа plot::Camera это может быть помещено в 3D сцену. Эти объекты камеры могут быть анимированы и позволить понимать “рейс” через 3D сцену. Смотрите раздел Cameras в 3D для деталей.
Ни один из атрибутов 2D coordinate systems и 3D coordinate systems может быть анимирован. Это включает поля просмотра, оси, метки деления осей и линии сетки (управления) в фоновом режиме. Смотрите страницы справки plot::CoordinateSystem2d и plot::CoordinateSystem3d для полного списка всех атрибутов для систем координат.
Несмотря на то, что ViewingBox атрибут системы координат не может быть анимирован, пользователь может все еще достигнуть анимированных эффектов видимости в 3D путем усечения объектов поля типа plot::ClippingBox.
Ни один из атрибутов, которые объявляются как “Тип Атрибута: наследованный” на их странице справки может быть анимирован. Это включает спецификации размера, такие как PointSize'LineWidth' и т.д.
RGB и значения RGBa не могут быть анимированы. Однако возможно анимировать окраску линий и поверхностей с помощью определяемых пользователем процедур. Смотрите страницы справки LineColorFunction и FillColorFunction для деталей.
Тексты аннотаций, такие как Footer, Headerзаголовок, legend entries, и т.д. не может быть анимирован. Положение titles, однако, может быть анимирован.
Существуют специальные текстовые объекты plot::Text2d и plot::Text3d это позволяет анимировать текст, а также их положение.
Шрифты не могут быть анимированы.
Приписывает, такие как DiscontinuitySearch = TRUE или FillPattern = Solid это может принять только конечно, что много значений от фиксированного дискретного набора не могут быть анимированы.
Почти все атрибуты, не попадающие в одну из этих категорий, могут быть анимированы. Вы найдете подробную информацию об этой проблеме о соответствующих страницах справки примитивов и атрибутов.
Как уже объяснено в разделе The Number of Frames и Области значений Времени, существуют “часы реального времени”, запускающиеся в фоновом режиме, который синхронизирует анимацию различных анимированных объектов.
Каждый анимированный объект имеет свою собственную отдельную “оперативную продолжительность жизни”, установленную атрибутами TimeBegin = t0, TimeEnd = t1 или, эквивалентно, TimeRange = t0..t1. Значения t0t1 представляйте секунды, измеренные “часами реального времени”.
В большинстве случаев нет никакой потребности обеспокоиться об определении продолжительности жизни. Если TimeBegin и TimeEnd не заданы, значения по умолчанию TimeBegin = 0 и TimeEnd = 10 используются, т.е. анимация продлится приблизительно 10 секунд. Эти значения только должны быть изменены
если более короткий или более длинный оперативный период для анимации желаем, или
если анимация содержит несколько анимированных объектов, где некоторые анимированные объекты должны остаться статическими, в то время как другие изменяются.
Вот пример для второй ситуации. График состоит из 3 переходящих точек. В течение первых 5 секунд подпрыгивает левая точка, в то время как другие точки остаются в своем исходном положении. Затем все точки остаются статическими в течение 1 секунды. После в общей сложности 6 секунд срединная точка запускает свою анимацию путем подпрыгивания, в то время как левая точка остается статической в своем конечном положении, и правые точки остается статическим в его исходном положении. После 9 секунд правая точка начинает перемещаться также. Полный отрезок времени для анимации является оболочкой областей значений времени всех анимированных объектов, т.е. 15 секунд в этом примере:
p1 := plot::Point2d(-1, sin(a), a = 0..PI, Color = RGB::Red,
PointSize = 5*unit::mm,
TimeBegin = 0, TimeEnd = 5):
p2 := plot::Point2d(0, sin(a), a = 0..PI, Color = RGB::Green,
PointSize = 5*unit::mm,
TimeBegin = 6, TimeEnd = 12):
p3 := plot::Point2d(1, sin(a), a = 0..PI, Color = RGB::Blue,
PointSize = 5*unit::mm,
TimeBegin = 9, TimeEnd = 15):
plot(p1, p2, p3, PointSize = 3.0*unit::mm,
YAxisVisible = FALSE):
Здесь, все точки используют настройки по умолчанию VisibleBeforeBegin = TRUE и VisibleAfterEnd = TRUE которые делают их видимыми как статические объекты вне области значений времени их анимации. Мы устанавливаем VisibleAfterEnd = FALSE для срединной точки, так, чтобы это исчезло после конца ее анимации. С VisibleBeforeBegin = FALSE, правая точка не отображается до ее запусков анимации:
p2::VisibleAfterEnd := FALSE:
p3::VisibleBeforeBegin := FALSE:
plot(p1, p2, p3, PointSize = 3.0*unit::mm,
YAxisVisible = FALSE):
Мы обобщаем модель синхронизации анимаций:
Общий оперативный промежуток анимированного графика является физическим реальным временем, данным минимумом TimeBegin значения всех анимированных объектов в графике к максимуму TimeEnd значения всех анимированных объектов.
Когда график, содержащий анимированные объекты, создается, часы реального времени установлены в минимум TimeBegin значения всех анимированных объектов в графике. Часы реального времени запускаются при требовании у кнопки 'игры' анимации в графическом интерфейсе пользователя.
Прежде чем реальное время достигает TimeBegin значение t0 из анимированного объекта этот объект является статическим в состоянии, соответствующем начинанию его анимации. В зависимости от атрибута VisibleBeforeBegin, это может отобразиться или быть невидимо перед t0.
В течение времени от t0 к t1, объект изменяется от его оригинала до его конечного состояния.
После того, как реальное время достигает TimeEnd значение t1, объект остается статическим в соответствии состояния в конец его анимации. В зависимости от значения атрибута VisibleAfterEnd, это может остаться видимым или становиться невидимым после t1.
Анимация целого графика заканчивается физическим временем, данным максимумом TimeEnd значения всех анимированных объектов в графике.
Существуют некоторые специальные атрибуты, такие как VisibleAfter это очень полезно, чтобы создать анимации из чисто статических объектов:
С VisibleAfter = t0, объект невидим от запуска анимации до времени t0. Затем это появится и останется видимым для остальной части анимации.
С VisibleBefore = t1, объект отображается от запуска анимации до времени t1. Затем это исчезнет и останется невидимым для остальной части анимации.
Эти атрибуты не должны быть объединены, чтобы задать “диапазон видимости” от t0 к t1. Используйте атрибут VisibleFromTo вместо этого:
С VisibleFromTo = t0..t1, объект невидим от запуска анимации до времени t0. Затем это появится и останется видимым до времени t1, когда это исчезнет и останется невидимым для остальной части анимации.
Мы продолжаем пример предыдущего раздела, в котором мы задали следующие анимированные точки:
p1 := plot::Point2d(-1, sin(a), a = 0..PI, Color = RGB::Red,
PointSize = 5*unit::mm,
TimeBegin = 0, TimeEnd = 5):
p2 := plot::Point2d(0, sin(a), a = 0..PI, Color = RGB::Green,
PointSize = 5*unit::mm,
TimeBegin = 6, TimeEnd = 12):
p3 := plot::Point2d(1, sin(a), a = 0..PI, Color = RGB::Blue,
PointSize = 5*unit::mm,
TimeBegin = 9, TimeEnd = 15):
p2::VisibleAfterEnd := FALSE:
p3::VisibleBeforeBegin := FALSE:Мы добавляем дальнейшую точку p4 это не анимировано. Мы делаем его невидимым в начале анимации через атрибут VisibleFromTo. Это сделано видимым после 7 секунд, чтобы исчезнуть снова после 13 секунд:
p4 := plot::Point2d(0.5, 0.5, Color = RGB::Black,
PointSize = 5*unit::mm,
VisibleFromTo = 7..13):Запуск анимации определяется p1 который переносит атрибут TimeBegin = 0, конец анимации определяется p3 который установил TimeEnd = 15:
plot(p1, p2, p3, p4, PointSize = 3.0*unit::mm,
YAxisVisible = FALSE):
Несмотря на то, что типичная анимация MuPAD сгенерирована объект объектом, каждый анимированный объект, заботящийся о его собственной анимации, мы можем также использовать атрибуты VisibleAfter, VisibleBefore, VisibleFromTo создавать кадр анимации системой координат:
“Система координат покадровыми анимациями”: Выберите набор (обычно статических) графических примитивов, которые должны отобразиться в i-th системой координат анимации. Установите VisibleFromTo = t[i]..t[i+1] для этих примитивов, где t[i]..t[i+1] оперативная продолжительность жизни i-th система координат (в секундах). Наконец, постройте все системы координат в одном plot команда.
Вот пример. Мы позволяем двум точкам блуждать вдоль графиков синуса и косинусной функции, соответственно. Каждая система координат должна состоять из изображения двух точек. Мы используем plot::Group2d задавать систему координат; группа вперед атрибут VisibleFromTo ко всем его элементам:
for i from 0 to 101 do
t[i] := i/10;
end_for:
for i from 0 to 100 do
x := i/100*PI;
myframe[i] := plot::Group2d(
plot::Point2d([x, sin(x)], Color = RGB::Red),
plot::Point2d([x, cos(x)], Color = RGB::Blue),
VisibleFromTo = t[i]..t[i + 1]);
end_for:
plot(myframe[i] $ i = 0..100, PointSize = 5.0*unit::mm):
Этой “системе координат системой координат” анимация, конечно, нужно немного больше усилия по кодированию, чем эквивалентная objectwise анимация, где каждая из точек анимирована:
delete i:
plot(plot::Point2d([i/100*PI, sin(i/100*PI)], i = 0..100,
Color = RGB::Red),
plot::Point2d([i/100*PI, cos(i/100*PI)], i = 0..100,
Color = RGB::Blue),
Frames = 101, TimeRange = 0..10,
PointSize = 5.0*unit::mm):
Существует, однако, специальный вид графика, где “система координат системой координат” анимации очень полезна. Обратите внимание на то, что в текущей версии графики, новые объекты графика не могут быть добавлены к сцене, которая уже представляется. Со специальными анимациями “видимости” для статических объектов, однако, можно легко симулировать график, который постепенно растет: Заполните системы координат анимации со статическими объектами, которые отображаются на ограниченный срок только. Видимость может быть выбрана очень гибко пользователем. Например, статические объекты могут быть сделаны видимыми только для одной системы координат (VisibleFromTo) так, чтобы объекты, казалось, перемещались.
В следующем примере мы используем VisibleAfter заполнять график постепенно. Мы демонстрируем каустик, сгенерированный солнечным светом в чашке чая. Оправа чашки, рассматриваемой как зеркало, дана функцией![]() , x ∈ [-1, 1] (полукруг). Лучи Sun, параллельные y - ось, отражаются оправой. После отражения в точке (x, f (x)) оправы, луч направляется в направление
, x ∈ [-1, 1] (полукруг). Лучи Sun, параллельные y - ось, отражаются оправой. После отражения в точке (x, f (x)) оправы, луч направляется в направление![]() , если x положителен. Это направляется в направление
, если x положителен. Это направляется в направление![]() , если x отрицателен. Развертываясь через зеркало слева направо, входящие лучи, а также отраженные лучи визуализируются как линии. В анимации они становятся видимыми после времени 5 x, где x является координатой точки оправы, в которой отражается луч:
, если x отрицателен. Развертываясь через зеркало слева направо, входящие лучи, а также отраженные лучи визуализируются как линии. В анимации они становятся видимыми после времени 5 x, где x является координатой точки оправы, в которой отражается луч:
f := x -> -sqrt(1 - x^2):
plot(// The static rim:
plot::Function2d(f(x), x = -1..1, Color = RGB::Black),
// The incoming rays:
plot::Line2d([x, 2], [x, f(x)], VisibleAfter = 5*x
) $ x in [-1 + i/20 $ i = 1..39],
// The reflected rays leaving to the right:
plot::Line2d([x, f(x)],
[1, f(x) + (1-x)*(f'(x) - 1/f'(x))/2],
Color = RGB::Orange, VisibleAfter = 5*x
) $ x in [-1 + i/20 $ i = 1..19],
// The reflected rays leaving to the left:
plot::Line2d([x, f(x)],
[-1, f(x) - (x+1)*(f'(x) - 1/f'(x))/2],
Color = RGB::Orange, VisibleAfter = 5*x
) $ x in [-1 + i/20 $ i = 21..39],
ViewingBox = [-1..1, -1..1]):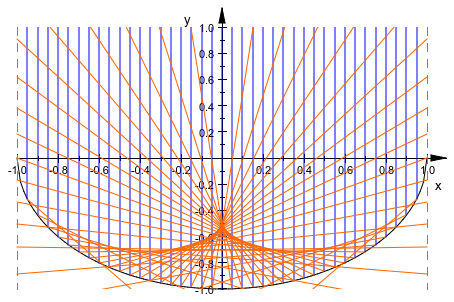
Сравните сферическое зеркало с параболическим зеркалом, которое имеет истинный центр:
f := x -> -1 + x^2:
plot(// The static rim:
plot::Function2d(f(x), x = -1..1, Color = RGB::Black),
// The incoming rays:
plot::Line2d([x, 2], [x, f(x)], VisibleAfter = 5*x
) $ x in [-1 + i/20 $ i = 1..39],
// The reflected rays leaving to the right:
plot::Line2d([x, f(x)],
[1, f(x) + (1-x)*(f'(x) - 1/f'(x))/2],
Color = RGB::Orange, VisibleAfter = 5*x
) $ x in [-1 + i/20 $ i = 1..19],
// The reflected rays leaving to the left:
plot::Line2d([x, f(x)],
[-1, f(x) - (x+1)*(f'(x) - 1/f'(x))/2],
Color = RGB::Orange, VisibleAfter = 5*x
) $ x in [-1 + i/20 $ i = 21..39],
ViewingBox = [-1..1, -1..1]):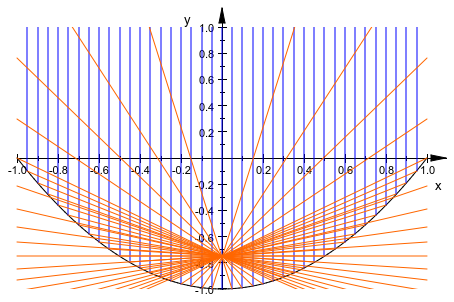
Мы создаем 2D анимацию, которая отображает функциональный f (x) вместе с интегралом![]() . Область между графиком f и x - ось отображена как анимированный объект штриховки. Текущее значение F (x) отображено анимированным текстом:
. Область между графиком f и x - ось отображена как анимированный объект штриховки. Текущее значение F (x) отображено анимированным текстом:
DIGITS := 2:
// the function:
f := x -> cos(x^2):
// the anti-derivative:
F := x -> numeric::int(f(y), y = 0..x):
// the graph of f(x):
g := plot::Function2d(f(x), x = 0..6, Color = RGB::Blue):
// the graph of F(x):
G := plot::Function2d(F(x), x = 0..6, Color = RGB::Black):
// a point moving along the graph of F(x):
p := plot::Point2d([a, F(a)], a = 0..6, Color = RGB::Black):
// hatched region between the origin and the moving point p:
h := plot::Hatch(g, 0, 0 ..a, a = 0..6, Color = RGB::Red):
// the right border line of the hatched region:
l := plot::Line2d([a, 0], [a, f(a)], a = 0..6,
Color = RGB::Red):
// a dashed vertical line from f to F:
L1 := plot::Line2d([a, f(a)], [a, F(a)], a = 0..6,
Color = RGB::Black, LineStyle = Dashed):
// a dashed horizontal line from the y axis to F:
L2 := plot::Line2d([-0.1, F(a)], [a, F(a)], a = 0..6,
Color = RGB::Black, LineStyle = Dashed):
// the current value of F at the moving point p:
t := plot::Text2d(a -> F(a), [-0.2, F(a)], a = 0..6,
HorizontalAlignment = Right):
plot(g, G, p, h, l, L1, L2, t,
YTicksNumber = None, YTicksAt = [-1, 1]):
delete DIGITS: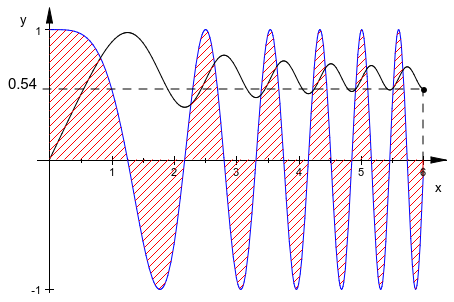
Мы создаем две 3D анимации. Первые запуски с прямоугольной полосой, которая деформирована к кольцу в x, плоскости y:
c := a -> 1/2 *(1 - 1/sin(PI/2*a)):
mycolor := (u, v, x, y, z) -> [(u - 0.8)/0.4, 0, (1.2 - u)/0.4]:
rectangle2annulus := plot::Surface(
[c(a) + (u - c(a))*cos(PI*v), (u - c(a))*sin(PI*v), 0],
u = 0.8..1.2, v = -a..a, a = 1/10^10..1,
FillColorFunction = mycolor, Mesh = [3, 40], Frames = 40):
plot(rectangle2annulus, Axes = None,
CameraDirection = [-11, -3, 3]):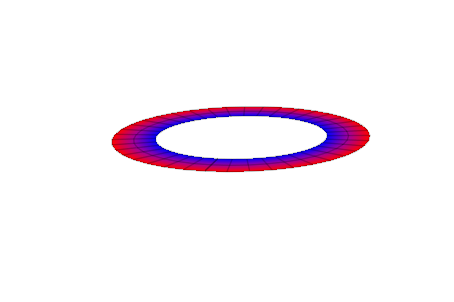
Вторая анимация скручивает кольцо, чтобы стать полосой Moebius:
annulus2moebius := plot::Surface(
[((u - 1)*cos(a*v*PI/2) + 1)*cos(PI*v),
((u - 1)*cos(a*v*PI/2) + 1)*sin(PI*v),
(u - 1)*sin(a*v*PI/2)],
u = 0.8..1.2, v = -1..1, a = 0..1,
FillColorFunction = mycolor, Mesh = [3, 40], Frames = 20):
plot(annulus2moebius, Axes = None,
CameraDirection = [-11, -3, 3]):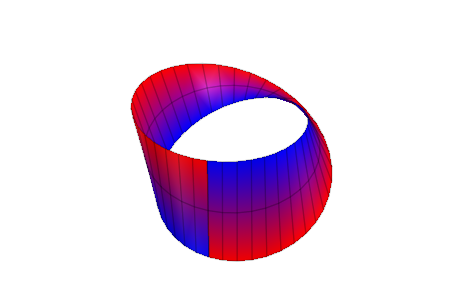
Обратите внимание на то, что последний кадр первой анимации совпадает с первой системой координат второй анимации. Чтобы соединить две отдельных анимации, мы можем установить соответствующие области значений видимости и построить их вместе. После 5 секунд первый объект Animation исчезает и вторые взятия:
rectangle2annulus::VisibleFromTo := 0..5:
annulus2moebius::VisibleFromTo := 5..7:
plot(rectangle2annulus, annulus2moebius, Axes = None,
CameraDirection = [-11, -3, 3]):
В этом примере мы рассматриваем плоские астрономические 3 проблемы тела. Мы решаем систему дифференциальных уравнений
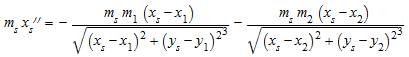 ,
,
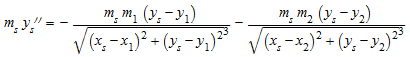 ,
,
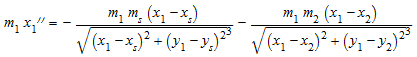 ,
,
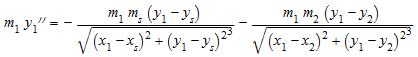 ,
,
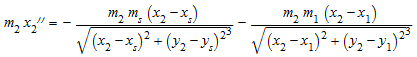 ,
,
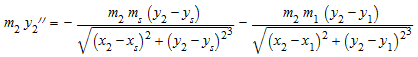 ,
,
который является только уравнениями движений для двух планет с массами m 1, m 2 в положениях (x 1, y 1), (x 2, y 2) вращающийся в x, плоскости y вокруг солнца массового m s, расположенный в (x s, y s). Мы задаем массовые отношения: первая планета является гигантом с массовым m 1, который составляет 4% массы солнца. Вторая планета намного меньше:
ms := 1: m1 := 0.04: m2 := 0.0001:
Как мы будем видеть, движение гиганта почти без помех небольшой планетой. Маленький, однако, в большой степени нарушен гигантом и, наконец, вышиблен из системы после близкого столкновения.
Мы решаем ОДУ через MuPAD, числовое ОДУ решает numeric::odesolve2 это обеспечивает вектор решения
![]() .
.
Начальные условия выбраны таким образом, что общий импульс исчезает, т.е. общий центр массы остается помещенным (в источнике):
Y := numeric::odesolve2(numeric::ode2vectorfield(
{xs''(t) =
-m1*(xs(t)-x1(t))/sqrt((xs(t)-x1(t))^2 + (ys(t)-y1(t))^2)^3
-m2*(xs(t)-x2(t))/sqrt((xs(t)-x2(t))^2 + (ys(t)-y2(t))^2)^3,
ys''(t) =
-m1*(ys(t)-y1(t))/sqrt((xs(t)-x1(t))^2 + (ys(t)-y1(t))^2)^3
-m2*(ys(t)-y2(t))/sqrt((xs(t)-x2(t))^2 + (ys(t)-y2(t))^2)^3,
x1''(t) =
-ms*(x1(t)-xs(t))/sqrt((x1(t)-xs(t))^2 + (y1(t)-ys(t))^2)^3
-m2*(x1(t)-x2(t))/sqrt((x1(t)-x2(t))^2 + (y1(t)-y2(t))^2)^3,
y1''(t) =
-ms*(y1(t)-ys(t))/sqrt((x1(t)-xs(t))^2 + (y1(t)-ys(t))^2)^3
-m2*(y1(t)-y2(t))/sqrt((x1(t)-x2(t))^2 + (y1(t)-y2(t))^2)^3,
x2''(t) =
-ms*(x2(t)-xs(t))/sqrt((x2(t)-xs(t))^2 + (y2(t)-ys(t))^2)^3
-m1*(x2(t)-x1(t))/sqrt((x2(t)-x1(t))^2 + (y2(t)-y1(t))^2)^3,
y2''(t) =
-ms*(y2(t)-ys(t))/sqrt((x2(t)-xs(t))^2 + (y2(t)-ys(t))^2)^3
-m1*(y2(t)-y1(t))/sqrt((x2(t)-x1(t))^2 + (y2(t)-y1(t))^2)^3,
xs(0) = -m1 , x1(0) = ms, x2(0) = 0,
ys(0) = 0.7*m2, y1(0) = 0, y2(0) = -0.7*ms,
xs'(0) = -1.01*m2, x1'(0) = 0, x2'(0) = 1.01*ms,
ys'(0) = -0.9*m1, y1'(0) = 0.9*ms, y2'(0) = 0},
[xs(t), xs'(t), ys(t), ys'(t),
x1(t), x1'(t), y1(t), y1'(t),
x2(t), x2'(t), y2(t), y2'(t)]
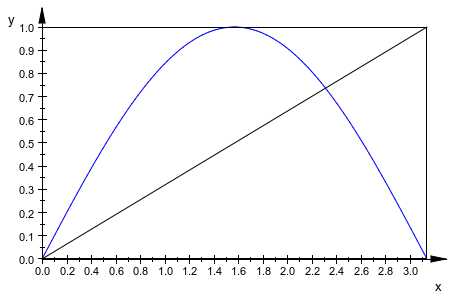
)):Положения [x s (t), y s (t)] = [Y(t)[1], Y(t)[3]], [x 1 (t), y 1 (t)] = [Y(t)[5], Y(t)[7]], [x 2 (t), y 2 (t)] = [Y(t)[9], Y(t)[11]] вычисляются на равноотстоящей mesh времени с dt = 0.05. Анимация создается “система координат системой координат” путем определения статических точек с подходящими значениями VisibleFromTo и статические линейные сегменты с подходящими значениями VisibleAfter.
Установка VisibleFromTo = t..t + 0.99*dt, каждая точка решения отображается только в течение короткого времени (факторный 0.99 убеждается, что не две точки могут отобразиться одновременно на каждой орбите). Орбиты точек поняты как линейные сегменты от положений во время t - dt к позициям во время t. Линейные сегменты становятся видимыми во время t и остаются видимыми для остальной части анимации (VisibleAfter = t), таким образом оставляя “след” движущихся точек. Мы получаем следующее графическое решение (расчет занимает приблизительно две минуты на компьютере на 1 ГГц):
dt := 0.05: imax := 516:
plot(// The sun:
plot::Point2d(Y(t)[1], Y(t)[3], Color = RGB::Orange,
VisibleFromTo = t..t + 0.99*dt,
PointSize = 4*unit::mm
) $ t in [i*dt $ i = 0..imax],
// The giant planet:
plot::Point2d(Y(t)[5], Y(t)[7], Color = RGB::Red,
VisibleFromTo = t..t + 0.99*dt,
PointSize = 3*unit::mm
) $ t in [i*dt $ i = 0..imax],
// The orbit of the giant planet:
plot::Line2d([Y(t - dt)[5], Y(t - dt)[7]],
[Y(t)[5], Y(t)[7]], Color = RGB::Red,
VisibleAfter = t
) $ t in [i*dt $ i = 1..imax],
// The small planet:
plot::Point2d(Y(t)[9], Y(t)[11], Color = RGB::Blue,
VisibleFromTo = t..t + 0.99*dt,
PointSize = 2*unit::mm
) $ t in [i*dt $ i = 0..imax],
// The orbit of the small planet:
plot::Line2d([Y(t - dt)[9], Y(t - dt)[11]],
[Y(t)[9], Y(t)[11]], Color = RGB::Blue,
VisibleAfter = t
) $ t in [i*dt $ i = 1..imax]
):