plot::LsysСистемы Lindenmayer
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
plot::Lsys(alpha, start, trans, …, <a = amin .. amax>, options)
plot::Lsys создает системы Lindenmayer, т.е. строку, переписывая системы, управляющие графикой с относительными командами.
Системы Lindenmayer или L-системы для краткости основаны на концепции итеративного преобразования строки символов в другую строку. После конечного числа итераций получившая строка переводится в последовательность команд перемещения “черепахе” (см. plot::Turtle), который может чертиться на экране.
В plot::Lsys, строка символов представлена строкой символов, т.е. DOM_STRING. Правила преобразования даны как уравнения, сопоставляющие строки длины 1 к строкам произвольной длины. Правила черепахи даны как уравнения, сопоставляющие строки длины 1 к простым командам перемещения: Lineперемещение, Left, Right, Push, Pop, Noop, или спецификация цветов.
Команды в основном очевидны. Left и Right поворот суммой установлен в пазе "RotationAngle"; начальное направление произошло. Line и Move перемещение суммой установлено в "StepLength", где Move не чертит линию. Push хранит текущее состояние (положение, направление, цвет) на стеке от того, где это может позже быть повторно активировано с помощью Pop. Noop означает, “игнорируют это, никакая операция”. Спецификация цветов изменяет цвет линии.
Следующие правила черепахи использованы по умолчанию (но может быть отключен путем предоставления других правил для левых сторон):
"F" = Line, "f" = Move, "[" = Push, "]" = Pop, "+" = Left, "-" = Right.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AffectViewingBox | влияние объектов на ViewingBox из сцены | TRUE |
AntiAliased | сглаженные линии и точки? | FALSE |
Color | основной цвет | RGB::Blue |
Frames | количество систем координат в анимации | 50 |
Generations | количество итераций L-системных правил | 5 |
IterationRules | правила итерации L-системы | |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | FALSE |
LineColor | цвет линий | RGB::Blue |
LineWidth | ширина линий | 0.35 |
LineStyle | тело, подчеркнутые штриховой линией или пунктирные линии? | Solid |
LinesVisible | видимость линий | TRUE |
Name | имя объекта графика (для браузера и легенды) | |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
RotationAngle | угол команд вращения в L-системах | |
StartRule | запустите правило L-системы | |
StepLength | продолжительность команд перемещения в L-системах | 1.0 |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11 |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
TurtleRules | правила, переводящие L-системные символы в перемещения черепахи | |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
Как очень простая система, мы рассматриваем следующее правило итерации: “замените каждую линию вперед последовательностью “линия вперед, продвиньтесь без рисования, линия вперед””.:
l := plot::Lsys(0, "F", "F" = "FfF"):
Обратите внимание на то, что мы не предоставляем правило итерации для "f". Это означает, “оставляют f один, не изменяйте его”.
Начальное состояние отображено путем графического вывода системы после нулевых поколений:
l::Generations := 0: plot(l)

Увеличивая число поколений, мы видим эффект нашего правила преобразования:
l::Generations := 1: plot(l)

l::Generations := 2: plot(l)

l::Generations := 3: plot(l)

Следующий вариант этого простого примера производит приближения для Канторова набора:
l := plot::Lsys(0, "F", "F" = "FfF", "f" = "fff"): plot(l)

Чтобы получить более интересные примеры, мы включаем вращения в наши правила:
l := plot::Lsys(PI/2, "F-F-F-F", "F" = "F-F+F+FF-F-F+F",
Generations = 3)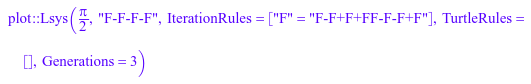
Как вы видите, plot::Lsys обнаружил, что наше правило является правилом итерации. Мы, возможно, использовали этот синтаксис непосредственно при создании объекта. Мы не дали правила черепахи, таким образом, значения по умолчанию используются:
plot(l)

Кривая Пеано является известным примером кривой заполнения пробела. В предельном процессе, увеличивая число итераций при уменьшении длины прямых шагов, это на самом деле заполняет плоскость. Существуют различные известные конструкции, один показанный здесь заполняет квадрат, наклоненный![]() :
:
peano := plot::Lsys(PI/2, "F", "F" = "F+F-F-F-F+F+F+F-F"):
Правило преобразования говорит, чтобы заменить каждую прямую линию на следующую конструкцию:
peano::Generations := 1: plot(peano)
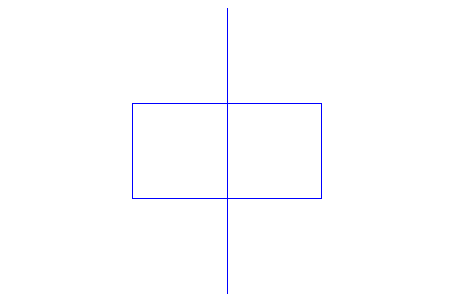
После нескольких итераций линии уже добираются очень друг близко к другу:
peano::Generations := 5: plot(peano)

Много L-систем содержат различные типы линий: В то время как они чертятся точно то же самое, их правила преобразования отличаются друг от друга. Следующий пример показывает изображение, похожее на Треугольник Серпинского:
l := plot::Lsys(PI/3, "R", "L" = "R+L+R", "R" = "L-R-L",
"L" = Line, "R" = Line,
Generations = 7):
plot(l)
Push и Pop операции могут использоваться, чтобы чертить “руки” в L-системе:
plot(plot::Lsys(23*PI/180, "F", "F" = "FF-[-F+F+F]+[+F-F-F]",
Generations = 4))
L-системы использовались, чтобы симулировать рост объекта. Мы показываем пример здесь, который использует символы BH, и G изменить цвет линий:
l := plot::Lsys(PI/9, "BL", "L" = "BR[+HL]BR[-GL]+HL",
"R" = "RR", "L" = Line, "R" = Line,
"B" = RGB::Brown, "H" = RGB::ForestGreen,
"G" = RGB::SpringGreen, Generations = 6):
plot(l)
Атрибут Generations может быть анимирован. Таким образом, мы можем на самом деле заставить “объект” “вырасти”:
plot(plot::Lsys(a*PI/45, "BL", "L" = "BR[+HL]BR[-GL]+HL", "R" = "RR",
"L" = Line, "R" = Line, "B" = RGB::Brown,
"H" = RGB::ForestGreen, "G" = RGB::SpringGreen,
Generations = a, a = 1 .. 6)):
L-системы могут отобразить несколько популярных фракталов. Одним примером является Снежинка Коха, сгенерированная, заменяя каждую прямую линию на прямую линию, сопровождаемую левым поворотом![]() , другую прямую линию, правый поворот
, другую прямую линию, правый поворот![]() , другую прямую линию, другой левый поворот
, другую прямую линию, другой левый поворот![]() и линию финишной прямой:
и линию финишной прямой:
koch := plot::Lsys(PI/3, "F--F--F", "F" = "F+F--F+F"):
Стартовое правило было выбрано, чтобы быть равносторонним треугольником:
koch::Generations := 0: plot(koch)

Первое поколение выглядит так:
koch::Generations := 1: plot(koch)

Предел вполне прилично аппроксимирован после пяти поколений:
koch::Generations := 5: plot(koch)

Наконец, мы используем plot::modify и "StepLength" паз, чтобы показать эти первые две итерации, наложенные друг на друга:
colors := [RGB::Red, RGB::Green, RGB::Blue, RGB::Yellow, RGB::DimGrey]:
plot(plot::modify(koch, Generations = i,
StepLength = 3^(-i),
LineColor = colors[i+1]) $ i = 0..4)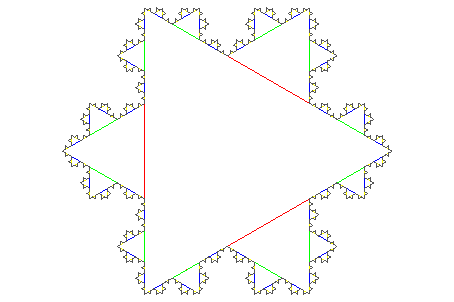
Другим известным примером фрактала, сгенерированного L-системой, является кривая Дракона Хивея. Неофициально, это сгенерировано путем “рисования прямого угла и затем заменяющий каждый прямой угол меньшим прямым углом” (Гарднер). Это использовалось в книге “Парк юрского периода” Майкла Крайтона и таким образом получило другой псевдоним, “фрактал Парка юрского периода”:
plot(plot::Lsys(PI/2, "L", "L" = "L+R+", "R" = "-L-R",
"L" = Line, "R" = Line, Generations = 9))
Интересно отметить, что правила итерации этой кривой эквивалентны добавлению зеркальной копии кривой к ее концу:
plot(plot::Lsys(PI/2, "L", "L" = "L+R+", "R" = "-L-R",
"L" = Line, "R" = Line, Generations = a,
a = 1..9))
В то время как L-система предыдущего примера соответствует определению, найденному в литературе, изображения по крайней мере в одном популярном источнике показывают другую систему (в то время как данным определением является то сверху), а именно:
plot(plot::Lsys(PI/4, "X-F-Y", "X" = "X+F+Y", "Y" = "X-F-Y",
"X" = Line, "Y" = Line, Generations = 9)):
L-система может содержать буквы, которые не предназначены, чтобы показать в итоговой диаграмме, таким образом, они формируют своего рода “маркеры” для последующего iteations. С этой целью можно использовать правило черепахи Noop:
plot(plot::Lsys(PI/12,
"X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X+X",
"X" = "[F+F+F+F[---X-Y]+++++F++++++++F-F-F-F]",
"Y" = "[F+F+F+F[---Y]+++++F++++++++F-F-F-F]",
"X" = Noop, "Y" = Noop,
Generations = 3))
plot(plot::Lsys(PI/2, "FB",
"A" = "FBFA+HFA+FB-FA", "B" = "FB+FA-FB-JFBFA",
"F" = "", "H" = "-", "J" = "+",
"A" = Noop, "B" = Noop, "H" = Noop, "J" = Noop))
Используя это правило, мы можем использовать следующую формулировку популярной Гильбертовой кривой из-за Кена Филипа:
plot(plot::Lsys(PI/2, "x", "x" = "-yF+xFx+Fy-", "y" = "+xF-yFy-Fx+",
"x" = Noop, "y" = Noop))
Чтобы анимировать процесс создания Гильбертовой кривой, мы настраиваем длину линий к текущему количеству шагов итерации:
plot(plot::Lsys(PI/2, "x", "x" = "-yF+xFx+Fy-", "y" = "+xF-yFy-Fx+",
"x" = Noop, "y" = Noop,
Generations = i, StepLength = 1/(2^i-1),
i = 1..6, Frames = 6))
В некоторых случаях системам будут нужны маленькие углы и длинные строки для того, чтобы задать желаемые направления. Возьмите, например, следующую систему:
plot(plot::Lsys(7*PI/15, "F", "F"="F+F--F+F",
Generations=4))
Вращения к праву используют угол![]() , в то время как это налево (резкий скачок) является поворотом
, в то время как это налево (резкий скачок) является поворотом![]() . Это выглядело бы более естественным, однако, чтобы иметь черепаху запускаются направо, т.е. под углом
. Это выглядело бы более естественным, однако, чтобы иметь черепаху запускаются направо, т.е. под углом![]() . Поскольку никакое кратное
. Поскольку никакое кратное![]() не равно
не равно![]() 2 π по модулю, это требует, чтобы мы использовали меньший угол, настраивая наше правило итерации:
2 π по модулю, это требует, чтобы мы использовали меньший угол, настраивая наше правило итерации:
plot(plot::Lsys(7*PI/30,"+++++++++++++++F",
"F"="F++F----F++F", Generations=4))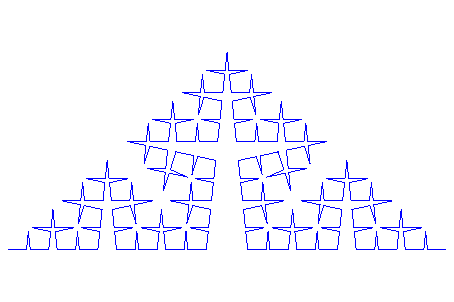
|
Угол (в радианах) для превращения команд. Animatable.
|
|
Строка используется в качестве стартового правила.
|
|
Итерация и правила команды Черепахи (см. ниже).
|
|
Параметр анимации, заданный как |
Системы Lindenmayer являются “системами перезаписи строки”. MuPAD® реализует только контекстно-свободные L-системы, которые анализируются в подобном контексте как бесконтекстные грамматики.
Много примеров L-систем могут быть найдены, среди других мест, во “Фрактальной Геометрии Природы” Бенуа Мандельбротом.