polylogФункция полилогарифма
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
polylog(n, x)
polylog(n,x) представляет функцию полилогарифма Li n (x) индекса n в точке x.
Для комплексного числа x модуля |x | <1, функция полилогарифма индекса n задан как
.
Эта функция расширена к целой комплексной плоскости аналитическим продолжением. Не путайте полилогарифмы Li n с интегральной функцией логарифма Li который отображен с помощью того же символа (без индекса).
Если n целое число и x число с плавающей запятой, затем результат с плавающей точкой вычисляется.
Если n целое число меньше или равный 1, затем явное выражение возвращено для любого входного параметра x. Если n целое число, больше, чем 1 или если n символьное выражение, затем неоцененный вызов polylog возвращен, если x число с плавающей запятой. Если n численное значение, но не целое число, затем ошибка происходит.
Некоторые специальные значения для n = 2 реализованы (cf. dilog). Значения Li n (0) = 0 и
реализованы для любого n. Кроме того,
для любого n ≠ 1.
Li n (x) имеет сингулярность в точке x = 1 для индексов n ≤ 1. Для индексов n ≥ 1, точка x = 1 является точкой разветвления. Разрез является действительным интервалом
. Скачок происходит при пересечении этого сокращения. См. Пример 2.
Математически, polylog(2,x) совпадает с dilog(1-x).
Когда названо аргументом x с плавающей точкой, функция чувствительна к переменной окружения DIGITS который определяет числовую рабочую точность.
Явные результаты возвращены для целочисленных индексов n ≤ 1:
polylog(-5, x), polylog(-1, x), polylog(0, x), polylog(1, x)
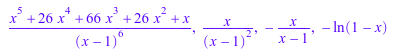
На неоцененный звонок отвечают, если индексом является целочисленный n> 1 или символьное выражение:
polylog(2, x), polylog(n^2 + 1, 2), polylog(n + 1, 2.0)
Значения с плавающей точкой вычисляются для целочисленных индексов n и аргументы x с плавающей точкой:
polylog(-5, -1.2), polylog(10, 100.0 + 3.2*I)
Реализованы некоторые специальные символьные значения:
polylog(4, 1), polylog(5, -1), polylog(2, I)
assume(n <> 1): polylog(n, -1)
unassume(n): polylog(n, -1)
Для индексов n ≥ 1, действительный интервал
является разрезом. Значения возвращены polylog перейдите при пересечении этого сокращения:
polylog(3, 1.2 + I/10^1000) - polylog(3, 1.2 - I/10^1000)
Функции diff, float, limit, и series обработайте выражения, включающие polylog:
diff(polylog(n, x), x), float(polylog(4, 3 + I))
series(polylog(4, sin(x)), x = 0)
|
Арифметическое выражение, представляющее целое число |
|
Арифметическое выражение.
x
Л. Льюин, “Полилогарифмы и связанные функции”, северная Голландия (1981). Л. Льюин (редактор)., “Структурные свойства полилогарифмов”, математическое издание 37 обзоров и монографий, американское математическое общество, провидение (1991).
Полилогарифмы характеризуются
в сочетании с Li n (0) = 0 и Li 1 (x) = - ln (1 - x). Li n (x) является рациональной функцией в x для n ≤ 0.
Li n имеет разрез вдоль действительного интервала
для индексов n ≥ 1. Значение в точке x на сокращении совпадает с пределом “снизу”:
.