`limit`

Вычислите предел

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

limit(f, x, <Left | Right | Real>, <Intervals>, <NoWarning>)
limit(f, x = x₀, <Left | Right | Real>, <Intervals>, <NoWarning>)

Описание

_{limit(f, x = x0, Real)} вычисляет двунаправленный предел.

_{limit(f, x = x0, Left | Right)} вычисляет односторонний предел, соответственно.

_{limit(f, x = x0, Intervals)} вычисляет набор, содержащий все предельные точки.

limit(f, x = x0, <Real>) вычисляет двунаправленный предел f когда x стремится к x0 на вещественной оси. Предельная точка x0 может быть не использован, в этом случае limit принимает x0 = 0.

Если предельная точка x0 infinity или - ∞, затем предел взят слева к infinity или справа к - ∞, соответственно.

Если доказуемо никакой предел не существует, то undefined возвращен. Смотрите Пример 2.

limit(f, x = x0, Left) возвращает предел когда x стремится к x0 слева. limit(f, x = x0, Right) возвращает предел когда x стремится к x0 справа. Смотрите Пример 2.

Если нельзя определить, существует ли предел или не может определить свое значение, то символьное limit возвращен. Смотрите Пример 3. То же самое содержит, в случае, если опция Intervals дан, если никакая информация на съемочной площадке предельных точек не могла бы быть получена.

Если f содержит параметры, затем limit реагирует на свойства тех параметров, установленных assume. Смотрите Пример 5. Это может также возвратить анализ случая (piecewise) в зависимости от этих параметров.

Можно вычислить предел кусочно-линейной функции. Условия, которые вы используете, чтобы задать кусочно-линейную функцию, могут зависеть от предельной переменной. Смотрите Пример 6.

Внутренне, limit попытки определить предел из последовательного расширения f вокруг x = x0 вычисленный через series. Может быть необходимо увеличить значение переменной окружения ORDER для того, чтобы найти предел.

Примечание

limit работает на символьном уровне и не должен быть вызван аргументами, содержащими аргументы с плавающей точкой.

Взаимодействия среды

Функция чувствительна к переменной окружения ORDER, который определяет количество по умолчанию условий в последовательных расчетах (см. series).

Свойства идентификаторов установлены assume учтены.

Примеры

Пример 1

Следующая команда вычисляет:

limit((1 - cos(x))/x^2, x)

Возможное определение e дано пределом последовательности для:

limit((1 + 1/n)^n, n = infinity)

Вот более комплексный пример:

limit(
  (exp(x*exp(-x)/(exp(-x) + exp(-2*x^2/(x+1)))) - exp(x))/x,
  x = infinity
)

Пример 2

Двунаправленный предел для не существует:

limit(1/x, x = 0)

Можно вычислить односторонние пределы слева и справа путем передачи опций Left и Right, соответственно:

limit(1/x, x = 0, Left), 
limit(1/x, x = 0, Right)

Пример 3

Если limit не может вычислить предел, затем символьный limit на звонок отвечают:

delete f: limit(f(x), x = infinity)

Пример 4

Функциональный sin (x) колеблется для между - 1 и 1; никакие предельные точки вне того интервала не существуют:

limit(sin(x), x = infinity, Intervals)

На самом деле все элементы возвращенного интервала являются предельными точками. Это не должно иметь место в целом. В следующем примере нижний предел и выше предел на самом деле и, соответственно:

limit(sin(1/x) + cos(1/x), x = 0, Intervals)

Пример 5

limit не может вычислить предел x ⁿ для без дополнительной информации о параметре n:

assume(n in R_): 
limit(x^n, x = infinity)

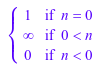
Мы можем также assume сразу тот n> 0 и не получает анализа случая затем:

assume(n > 0): limit(x^n, x = infinity)

Точно так же мы можем принять что n <0:

assume(n < 0): limit(x^n, x = infinity)

delete n:

Пример 6

Вычислите предел кусочно-линейной функции:

limit(piecewise([x^3 > 10000*x, 1/x],
                [x^3 <= 10000*x, 10]),
                            x = infinity)

Пример 7

Вычислите пределы неполной Гамма функции:

limit(igamma(z, t), t = infinity);
limit(igamma(z, t), t = 0)

Параметры

`f`	Арифметическое выражение, представляющее функцию в `x`
`x`	Идентификатор
`_x0`	Предельная точка: арифметическое выражение, возможно `infinity` или `-infinity`

Опции

`Leftдействительный`, `Right`	Это управляет направлением предельного расчета. Опция `Real` случай по умолчанию и означает двунаправленный предел (т.е. нет никакой потребности задать эту опцию).
`Intervals`	Любой `TRUE` или `FALSE`, `FALSE` по умолчанию. Если эта опция установлена в `TRUE`, затем надмножество набора всех предельных точек возвращено. Если результат содержит только один элемент, тот элемент является пределом; с другой стороны, если это содержит больше элементов, не все они - обязательно предельные точки, такие, что предел может, тем не менее, существовать.
`NoWarning`	Если эта опция установлена в `TRUE`, никакие предупреждающие сообщения не распечатаны на экране. Значением по умолчанию является `FALSE`.

Возвращаемые значения

арифметическое выражение. Если опция Intervals был дан, результат (конечен или бесконечен) набор.

Перегруженный

f

Алгоритмы

limit использует алгоритм на основе тезиса Доминика Грунца: “При Вычислении Пределов в Символьной Системе Манипуляции”, Швейцарская высшая техническая школа, Цюрих, Швейцария, 1995. Если это перестало работать, это пытается продолжить рекурсивно; наконец, это делает попытку последовательного расширения.

Документация