`stats`::`ksGOFT`

Тест качества подгонки Кольмогорова-Смирнова

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

stats::ksGOFT(x₁, x₂, …, CDF = f)
stats::ksGOFT([x₁, x₂, …], CDF = f)
stats::ksGOFT(s, <c>, CDF = f)

Описание

stats::ksGOFT([x ₁, x ₂, …], CDF = f), применяет тест качества подгонки Кольмогорова-Смирнова для нулевой гипотезы: “x ₁, x ₂, … является f- распределенная выборка”.

Внешние статистические данные, сохраненные в ASCII-файле, могут быть импортированы в сеанс MuPAD^® через import::readdata. В частности, смотрите Пример 1 из соответствующей страницы справки.

Ошибка повышена, если какие-либо из данных не могут быть преобразованы в действительное число с плавающей запятой.

Позвольте y ₁, …, y _n быть входными данными x ₁, …, x _n, расположенный в порядке возрастания. stats::ksGOFT возвращает список

содержа следующую информацию:

K1 статистическая величина Кольмогорова-Смирнова.
p1 наблюдаемый уровень значения статистического K1.
K2 статистическая величина Кольмогорова-Смирнова.
p2 наблюдаемый уровень значения статистического K2.

Для статистической величины Кольмогорова-Смирнова K, соответствующий K1 или K2, соответственно, наблюдаемым уровням значения p1, p2 вычисляются асимптотическим приближением точной вероятности

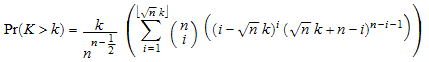Для большого n эти вероятности аппроксимированы

Таким образом, наблюдаемые уровни значения, возвращенные stats::ksGOFT аппроксимируйте точные вероятности для большого n. Примерно разговор, для n = 10, 3 ведущих цифры p1, p2 соответствуйте точным вероятностям. Для n = 100, 4 ведущих цифры p1, p2 соответствуйте точным вероятностям. Для n = 1000, 6 ведущих цифр p1, p2 соответствуйте точным вероятностям.

Наблюдаемый уровень значения PValue1 = p1 возвращенный stats::ksGOFT должен быть интерпретирован следующим образом:

По нулевой гипотезе вероятность p1 = не должен быть малым Pr (K> K1). А именно, p1 = Pr (K> K1) ≥ α должен содержать для данного уровня значения. Если это условие нарушено, гипотеза может быть отклонена на уровне α.

Таким образом, если наблюдаемый уровень значения p1 = Pr (K> K1) удовлетворяет p1 <α, демонстрационное продвижение к значению K1 из статистического K представляет маловероятное событие, и нулевые гипотезы могут быть отклонены на уровне α.

Соответствующая интерпретация содержит для PValue2 = p2: если p2 = Pr(K > K2) удовлетворяет p2 <α, нулевые гипотезы могут быть отклонены на уровне α.

Обратите внимание на то, что оба наблюдаемых уровня значения p1, p2 должно быть достаточно большим, чтобы заставить данные пройти тест. Нулевая гипотеза может быть отклонена на уровне α, если какое-либо из этих двух значений меньше, чем α.

Если p1 и p2 оба близко к 1, это должно вызвать подозрение о случайности данных: они указывают на подгонку, которая слишком хороша.

Распределения, которые не обеспечиваются stats- пакет может быть реализован легко пользователем. Определяемая пользователем процедура f может реализовать любую кумулятивную функцию распределения; stats::ksGOFT вызовы f (x) с действительными аргументами с плавающей точкой от выборки данных. Функциональный f должен возвратить числовое действительное значение между 0 и 1. См. Пример 3.

Взаимодействия среды

Функция чувствительна к переменной окружения DIGITS который определяет числовую рабочую точность.

Примеры

Пример 1

Мы создаем выборку 1 000 нормально распределенных случайных чисел:

r := stats::normalRandom(0, 1, Seed = 123):
data := [r() $ i = 1 .. 1000]:

Мы тестируем, нормально распределены ли эти данные действительно со средним значением 0 und отклонений 1. Мы передаем соответствующую кумулятивную функцию распределения stats::normalCDF(0, 1) к stats::ksGOFT:

stats::ksGOFT(data, CDF = stats::normalCDF(0, 1))

Результат показывает, что данные могут быть приняты как выборка нормально распределенных чисел: оба наблюдаемых уровня значения и не малы.

Затем мы вводим некоторые дальнейшие данные в выборку:

data := data . [frandom() $ i = 1..100]:
stats::ksGOFT(data, CDF = stats::normalCDF(0, 1))

Теперь данные не должны быть приняты как выборка нормальных отклонений со средним значением 0 и отклонением 1, потому что второй наблюдаемый уровень значения PValue2 очень мал.

delete r, data:

Пример 2

Мы создаем выборку, состоящую из одного столбца строки и двух столбцов нестроки:

s := stats::sample(
  [["1996", 1242, PI - 1/2], ["1997", 1353, PI + 0.3],
   ["1998", 1142, PI + 0.5], ["1999", 1201, PI - 1],
   ["2001", 1201, PI]])

"1996"  1242  PI - 1/2
"1997"  1353  PI + 0.3
"1998"  1142  PI + 0.5
"1999"  1201    PI - 1
"2001"  1201        PI

Мы рассматриваем данные в третьем столбце. Среднее значение и отклонение этих данных вычисляются:

[m, v] := [stats::mean(s, 3), stats::variance(s, 3)]

Мы проверяем, нормально распределены ли данные 3-го столбца со средним значением и отклонением, вычисленным выше:

stats::ksGOFT(s, 3, CDF = stats::normalCDF(m, v))

Оба наблюдаемых уровня значения и возвратились тестом, не малы. Нет никакой причины отклонить нулевую гипотезу, что данные нормально распределены.

delete s, m, v:

Пример 3

Мы демонстрируем, как могут использоваться пользовательские функции распределения. Следующая функция представляет кумулятивную функцию распределения Pr (X ≤ x) = x ² из переменной X, поддержанной на интервале [0, 1]. Это будет вызвано аргументами x с плавающей точкой и должно возвратить численные значения между 0 и 1:

f := proc(x) 
     begin
       if x <= 0 then return(0)
       elif x < 1 then return(x^2)
       else return(1)
       end_if
     end_proc:

Мы тестируем гипотезу, что следующими данными является f - распределенный:

data := [sqrt(frandom()) $ k = 1..10^2]:
stats::ksGOFT(data, CDF = f)

На данном уровне значения 0,1, скажем, не должна быть отклонена гипотеза: оба наблюдаемых уровня значения p1 = и p2 = превысьте 0.1.

delete f, data:

Параметры

`_{x1, x2, …}`	Статистические данные: действительные численные значения
`f`	Процедура, представляющая кумулятивную функцию распределения. Как правило, одна из функций распределения `stats`- пакет, такой как `stats::normalCDF`(n, v) и т.д.
`s`	Выборка доменного типа `stats::sample`
`c`	Целое число, представляющее индекс столбца демонстрационного `s`. Этот столбец предоставляет данным `x1x2` и т.д. Нет никакой потребности задать номер столбца `c` если выборка имеет только один столбец.

Возвращаемые значения

Перечислите четырьмя уравнениями [PValue1 = p1, StatValue1 = K1, PValue2 = p2, StatValue2 = K2], со значениями с плавающей точкой p1, K1, p2, K2. Смотрите раздел “Details” ниже для интерпретации этих значений.

Ссылки

Д. Э. Нут, Искусство Программирования, Vol 2: получисловые Алгоритмы, стр 48. Аддисон-Уэсли (1998).

Документация